递归算法与数据结构：如何在Java中设计和使用栈

# 1. 递归算法与数据结构简介

## 简介
递归算法是一种在解决问题时，函数自我调用的编程技术。它将大问题分解为相似的小问题，直到达到可以直接解决的简单情况。递归算法与数据结构紧密相连，尤其在处理具有自然递归结构的数据时，比如树和图。

## 数据结构的必要性
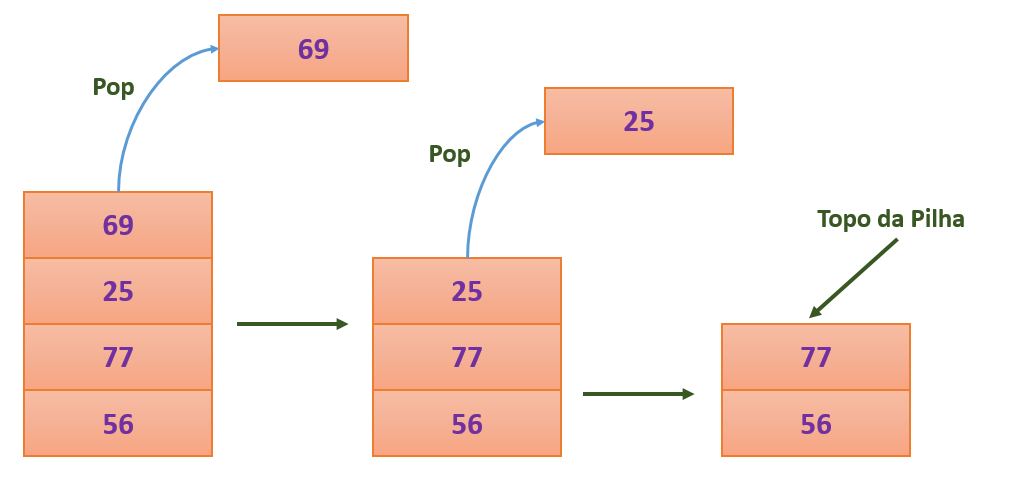
在编程中，数据结构是组织和存储数据的一种方式，以便可以有效地使用数据。递归算法经常与特定的数据结构——栈，紧密配合使用。栈是一种后进先出（LIFO）的数据结构，它支持两种主要操作：push（入栈）和pop（出栈）。

## 递归与数据结构的关联
理解递归算法和数据结构之间的关系对于设计有效的算法至关重要。例如，在树的遍历中，递归方法可以利用栈的特性来处理节点，实现深度优先搜索（DFS）。在本系列文章中，我们将探讨递归算法与栈的结合应用，以及它们在解决各种复杂问题中的作用。我们将从递归算法的基本原理开始，逐渐深入到数据结构的细节，并提供实际案例分析。

# 2. 递归算法基础

### 2.1 递归的定义和原理
#### 2.1.1 递归的概念
递归是一种在解决问题时反复调用自身的方法。它允许问题被分解为更小的相似子问题，并且可以通过简单的重复调用以达到问题解决的目的。在递归方法中，必须有终止条件来防止无限循环，这些终止条件定义了递归何时停止。

递归方法通常包含两个部分：基本情况（递归的停止条件）和递归情况（调用自身解决问题的更小实例）。以下是一个简单的递归函数例子，用Python语言计算阶乘：

def factorial(n):
    # 基本情况：0! = 1
    if n == 0:
        return 1
    # 递归情况：n! = n * (n-1)!
    else:
        return n * factorial(n-1)

#### 2.1.2 递归的实现机制
递归的实现机制通常涉及到函数调用栈。每次递归调用都会产生一个新的函数调用上下文，并将其压入栈中。在递归函数中，每一次递归调用都携带了一部分问题的状态信息。

当递归函数执行时，如果达到了基本情况，它会返回一个结果，该结果将用于解决上一层的递归调用。这个过程持续到最初的调用，最终返回到最初的问题的解决方案。递归的这种机制可以在简单的代码结构中解决复杂的问题，但同时也引入了调用栈的内存使用问题。

### 2.2 递归算法的设计
#### 2.2.1 设计递归算法的步骤
设计递归算法通常遵循以下步骤：
1. 定义问题的最小有效规模（基本情况）。
2. 确定如何将问题规模减小，并递归地调用算法自身。
3. 确保每一次递归调用都在逼近基本情况，并最终到达基本情况以避免无限递归。
4. 组合递归调用的结果以形成问题的最终解。

#### 2.2.2 递归算法的时间复杂度分析
递归算法的时间复杂度分析往往比较复杂，因为它取决于递归树的深度和每个节点的复杂度。递归树的深度等于递归调用的最大层数，而每个节点的复杂度通常与解决该层子问题所需要的时间成正比。

递归算法的时间复杂度通常用大O表示法来描述，例如，二分搜索算法的递归实现的时间复杂度为O(log n)，而阶乘函数的时间复杂度则为O(n)。

### 2.3 递归与迭代的比较
#### 2.3.1 递归与迭代的区别
递归是一种“分而治之”的问题解决策略，而迭代则是通过重复利用循环结构来逐步逼近问题的解决方法。

递归方法的优势在于代码清晰简洁，易于理解和实现。它在处理树形结构或者需要回溯的问题时特别有用。然而，递归方法可能引起较高的内存开销，因为它需要维护调用栈。

迭代方法通常在性能上更优，特别是在处理简单的线性问题时，因为迭代不需要额外的函数调用开销。它通常使用较少的内存，并且易于优化。然而，迭代的代码可能不如递归直观和简洁。

#### 2.3.2 递归到迭代的转换技巧
将递归算法转换为迭代算法可以提高内存效率并减少栈溢出的风险。以下是一种常见的转换技巧：

1. 使用循环来模拟递归过程。
2. 引入辅助数据结构（如栈）来存储子问题的状态信息，这模拟了递归调用栈的功能。
3. 逐步执行循环，并更新辅助数据结构，直到问题被解决。

举一个例子，我们用迭代方法来重新实现阶乘函数：

def factorial_iterative(n):
    result = 1
    while n > 0:
        result *= n
        n -= 1
    return result

在这个迭代版本中，我们用一个循环来代替了递归函数，避免了额外的函数调用开销。这种方式非常适合于尾递归优化，即递归调用是函数体中的最后一个操作。在支持尾递归优化的编程语言中，可以将递归算法改写为尾递归形式来实现迭代的效果。

# 3. 栈数据结构

## 3.1 栈的定义和特性

### 3.1.1 栈的概念

栈是一种抽象数据类型（ADT），它具有后进先出（LIFO, Last In First Out）的特性。这种特性意味着最后一个添加到栈中的元素将是第一个被移除的。想象一下，当你在桌面上堆叠盘子时，总是从顶部拿起盘子；这正是栈的工作方式。在计算机科学中，栈被用于管理函数调用、存储临时变量、进行表达式求值等许多任务。

### 3.1.2 栈的操作与性质

栈的操作主要有两种：`push`（入栈）和`pop`（出栈）。`push`操作将一个元素添加到栈顶，而`pop`操作则移除栈顶元素。栈可能还包括一个`peek`（查看栈顶元素）操作，该操作返回栈顶元素的值但不将其移除。

栈的性质如下：

- **后进先出（LIFO）：** 最后进入的元素最先被访问和移除。
- **访问限制：** 只能从一端添加或删除元素，这通常被称为“栈顶”。
- **容量限制：** 栈可能有固定的容量限制，到达限制时再进行`push`操作将会失败。

## 3.2 栈的实现

### 3.2.1 数组实现栈

使用数组实现栈是最常见的方法之一。数组栈由一系列相邻的内存空间组成，具有固定的容量。以下是一个简单的数组实现栈的示例代码：

public class ArrayStack {
    private int[] stackArray;
    private int top;
    private int maxSize;

    public ArrayStack(int size) {
        stackArray = new int[size];
        maxSize = size;
        top = -1;
    }

    public void push(int value) {
        if (top < maxSize - 1) {
            stackArray[++top] = value;
        } else {
            throw new RuntimeException("Stack is full");
        }
    }

    public int pop() {
        if (top > -1) {
            return stackArray[top--];
        } else {
            throw new RuntimeException("Stack is empty");
        }
    }

    public int peek() {
        if (top > -1) {
            return stackArray[top];
        } else {
            throw new RuntimeException("Stack is empty");
        }
    }

    public boolean isEmpty() {
        return top == -1;
    }
}

### 3.2.2 链表实现栈

另一种实现栈的方式是使用链表。链表实现的栈提供了动态容量扩展的优点，但增加了额外的内存开销，因为每个元素都需要存储指向下一项的指针。以下是一个简单的链表实现栈的示例代码：

public class LinkedStack {
    private Node top;

    public void push(int value) {
        Node newNode = new Node(value);
        newNode.next = top;
        top = newNode;
    }

    public int pop() {
        if (top != null) {
            Node temp = top;
            top = top.next;
            return temp.data;
        } else {
            throw new RuntimeException("Stack is empty");
        }
    }

    private class Node {
        private int data;
        private Node next;

        public Node(int data) {
            this.data = data;
            this.next = null;
        }
    }
}

## 3.3 栈的应用场景

### 3.3.1 函数调用栈

函数调用栈是栈在计算机程序中最常见的用途之一。每当调用一个函数时，它的参数、局部变量和返回地址会被压入栈中。当函数返回时，这些信息则被弹出栈，继续执行调用者的代码。栈在此场景中跟踪了函数调用的历史和状态。

### 3.3.2 表达式求值

栈在表达式求值，尤其是后缀表达式求值中发挥着重要作用。后缀表达式（逆波兰表示法）不需要括号来表示运算顺序，可以通过使用栈来解析。每个操作数被推入栈中，每个操作符则弹出栈顶的两个元素，计算结果后再次推入栈中。

### 3.3.3 括号匹配问题

括号匹配是栈的一个经典应用场景。通过将每遇到的左括号入栈，每遇到右括号则比较栈顶的左括号，可以有效地检查一个字符串中的所有括号是否正确匹配。这个问题在编程语言的解析和编译中非常重要。

以上内容介绍了栈的定义、特性、实现方式，以及在不同场景下的应用。本章节的深入探讨为理解递归算法与栈的结合应用奠定了基础。

# 4. Java中栈的使用和设计

## 4.1 Java中的内置栈类

### 4.1.1 Stack类的使用

Java提供了一个内置的栈类`java.util.Stack`，它继承自`Vector`类并提供了一组标准的栈操作。栈是一种后进先出（LIFO）的数据结构，支持基本操作如`push`（压入）、`pop`（弹出）、`peek`（查看栈顶元素）和`empty`（检查栈是否为空）。

要使用`Stack`类，首先需要导入`java.util`包中的相关类。下面的例子展示了如何创建一个`Stack`对象，并执行一些基本操作：

import java.util.Stack;

public class StackExample {
    public static void main(String[] args) {
        Stack<Integer> stack = new Stack<>();

        // push elements onto the stack
        stack.push(1);
        stack.push(2)