散列表优化术：提升数据查找速度的策略全览


# 摘要
散列表是一种高效的数据结构，广泛应用于各种计算领域，用于实现快速的键值查找。本文首先探讨了散列表的原理与应用场景，然后深入分析了散列表设计的关键要点，包括散列函数的选择、冲突解决策略和动态扩容技术。此外，本文还涉及了散列表的高级数据结构，如自平衡二叉搜索树、跳表和哈希表的变种结构，并提出了实际应用中的性能优化实践。最后，本文展望了散列表在现代处理器架构和分布式系统中的优化和应用，以及未来理论研究的方向和挑战。

# 关键字
散列表；散列函数；冲突解决；动态扩容；性能优化；自平衡二叉搜索树

参考资源链接：[数据结构1800题详解：考研&自学必备](https://wenku.csdn.net/doc/6469ced0543f844488c330fd?spm=1055.2635.3001.10343)
# 1. 散列表的原理与应用场景

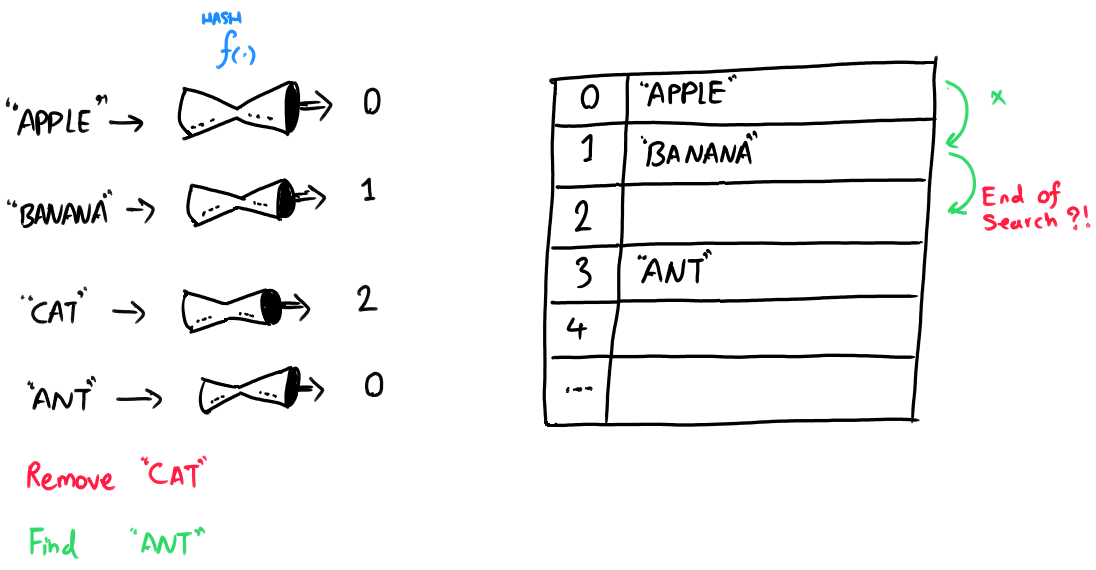
散列表（Hash Table），在计算机科学领域中，是一种以键值对（Key-Value Pair）存储数据的数据结构。它利用一个散列函数（Hash Function）将键映射到存储桶（Bucket），以快速定位到数据。散列表的设计旨在将数据的存储位置和其内容关联起来，从而在查找、插入和删除等操作中达到接近常数时间（O(1)）的效率。

## 1.1 散列表的基本原理

散列表的工作原理基于直接寻址表的概念，通过散列函数来计算键的哈希值，并根据该哈希值快速定位数据。当出现两个键对应相同的哈希值时，就会发生冲突，此时需要解决策略来处理这些冲突，确保每个桶中只有一项数据。

## 1.2 散列表的应用场景

散列表广泛应用于各类软件系统中，例如：
- **编译器的符号表**：用于存储变量及其属性。
- **数据库索引**：散列索引提供快速的查找和存储。
- **缓存机制**：如HTTP缓存、DNS缓存。
- **哈希表**：用于存储大量数据，利用散列函数减少数据之间的依赖。
- **搜索引擎**：用于快速检索网页和内容。

散列表在实际应用中的关键点包括选择合适的散列函数、有效的冲突解决策略和适当的动态扩容策略。在后续章节中，我们将深入探讨这些设计要点，以及散列表在不同场景中的优化实践和未来展望。

# 2. 散列表的设计要点

## 2.1 散列函数的选择与设计

### 2.1.1 理解散列函数的原理

散列函数是散列表的基础，它的主要任务是将输入（通常是各种数据类型）映射到一个整数。这个整数的范围通常在散列表大小之内，用于确定数据在表中的存储位置。一个好的散列函数要求输出分布均匀，使得数据尽可能随机地分布在整个表中，减少冲突，提高搜索效率。

设计散列函数时需要遵循的几个基本原则：
- **确定性**：相同的输入应该产生相同的输出。
- **高效性**：计算散列值应该快速。
- **均匀性**：不同的输入应产生均匀分布的散列值，以避免冲突。
- **简明性**：散列函数应该尽可能简单，易于理解和实现。

### 2.1.2 设计高效的散列函数

设计高效的散列函数要考虑数据的特性。例如，对于字符串类型的散列函数，通常需要考虑字符串中每个字符的权重。一个常用的散列函数是通过对字符串中每个字符的ASCII值进行运算，例如乘法散列法（Horner's Method）：

unsigned int hash(const char *str) {
    unsigned int hash = 0;
    unsigned int i = 0;
    while (str[i] != '\0') {
        hash = hash * 33 + str[i];
        i++;
    }
    return hash;
}

上述代码中，我们假设输入是一个以null结尾的字符串`str`。我们从第一个字符开始，将当前的`hash`值乘以33然后加上字符的ASCII值。这个过程循环进行，直到字符串结束。

### 2.1.3 散列函数的性能考量

对于散列函数的性能考量，关键指标是**装载因子**和**冲突率**。装载因子是当前存储的数据量与表容量的比值。装载因子低则表明散列表中的空位多，冲突的概率相应降低。冲突率是实际发生冲突的次数与插入操作总数的比值。如果冲突率较高，那么性能会下降，因为需要更多的操作来解决冲突。

## 2.2 冲突解决策略

### 2.2.1 冲突的定义及类型

在散列表中，冲突是指不同的输入数据通过散列函数计算后得到相同的索引值。冲突处理不当会导致性能下降，特别是当装载因子过高时。常见的冲突类型有：
- **同义词冲突**：两个不同的输入通过散列函数得到相同的索引。
- **堆积冲突**：如果散列函数不够好，或者装载因子过高，可能会造成连续的几个不同输入连续冲突，形成冲突链。

### 2.2.2 开放寻址法的实现与分析

开放寻址法是一种解决冲突的策略，当冲突发生时，会在表中寻找下一个空位。最简单的开放寻址法是线性探测，即从冲突位置开始，顺序查找下一个空位：

unsigned int search(unsigned int *table, unsigned int index, unsigned int size) {
    unsigned int i = 0;
    while (table[(index + i) % size] != 0 && i < size) {
        i++;
    }
    return (index + i) % size;
}

这段代码中，`table`是散列表数组，`index`是通过散列函数计算得到的索引，`size`是散列表的大小。如果当前索引位置已经被占用，则向后探测下一个空位。线性探测简单但容易形成堆积冲突。

### 2.2.3 链表法的实现与分析

链表法是另一种常用的冲突解决策略，它在每个索引位置存储一个链表，所有冲突的元素都放入这个链表。这种方法允许散列表保持较低的装载因子，因为表不需要预留额外空间来解决冲突：

struct HashEntry {
    int key;
    int value;
    struct HashEntry *next;
};

struct HashTable {
    struct HashEntry **table;
    int size;
};

void insert(struct HashTable *table, int key, int value) {
    int index = key % table->size;
    struct HashEntry *entry = malloc(sizeof(struct HashEntry));
    entry->key = key;
    entry->value = value;
    entry->next = table->table[index];
    table->table[index] = entry;
}

这段代码实现了链表法的基本操作，`insert`函数将一个新的键值对加入散列表。使用链表法时，虽然每个索引位置可能有多条链，但是由于链表操作通常都是O(1)的，因此散列表的整体性能仍然可以保持很好。然而，这种方法会增加存储空间的使用，并增加复杂性，因为它需要维护额外的链表结构。

# 3. 散列表的高级数据结构

## 3.1 自平衡二叉搜索树

### 3.1.1 红黑树的原理与特性

红黑树是一种自平衡的二叉搜索树，它的每一个节点都遵循红黑性质，确保树大致平衡，从而保证操作的时间复杂度在最坏情况下仍为 O(log n)。红黑树的五个性质如下：

1. 每个节点要么是红色，要么是黑色。
2. 根节点是黑色。
3. 所有叶子节点（NIL节点，空节点）都是黑色。
4. 每个红色节点的两个子节点都是黑色（从每个叶子到根的所有路径上不能有两个连续的红色节