编译原理中的数据流分析：习题案例分析与深入解读


参考资源链接：[《编译原理》第三版 陈火旺 课后习题答案详解](https://wenku.csdn.net/doc/5zv4rf8r76?spm=1055.2635.3001.10343)
# 1. 数据流分析的基础概念

数据流分析是一种用于编译器优化和程序理解的技术。其核心在于追踪程序中数据的流动情况，对变量值的产生、使用和传播进行分析。这项技术广泛应用在编译器设计中，目的是识别程序中可能的优化机会和潜在的错误。

## 数据流信息的类型

数据流信息可以分为两类：方向性信息（如定义、使用）和值集信息（如变量可能的值集合）。根据分析粒度的不同，数据流信息又可以细分为精确流敏感分析和近似流敏感分析。

## 数据流分析的应用场景

在软件工程中，数据流分析技术用于静态分析代码、验证程序正确性、进行代码优化等。而在程序运行时，动态数据流分析可用于监控、调试和性能分析。

通过掌握这些基础概念，IT行业的专业人员可以更深入地理解数据流分析如何增强软件质量，并提升系统运行效率。接下来的章节将进一步探讨其理论基础和求解方法。

# 2. 数据流分析的理论基础

## 2.1 数据流方程和算法概述

### 2.1.1 数据流方程的定义和类型

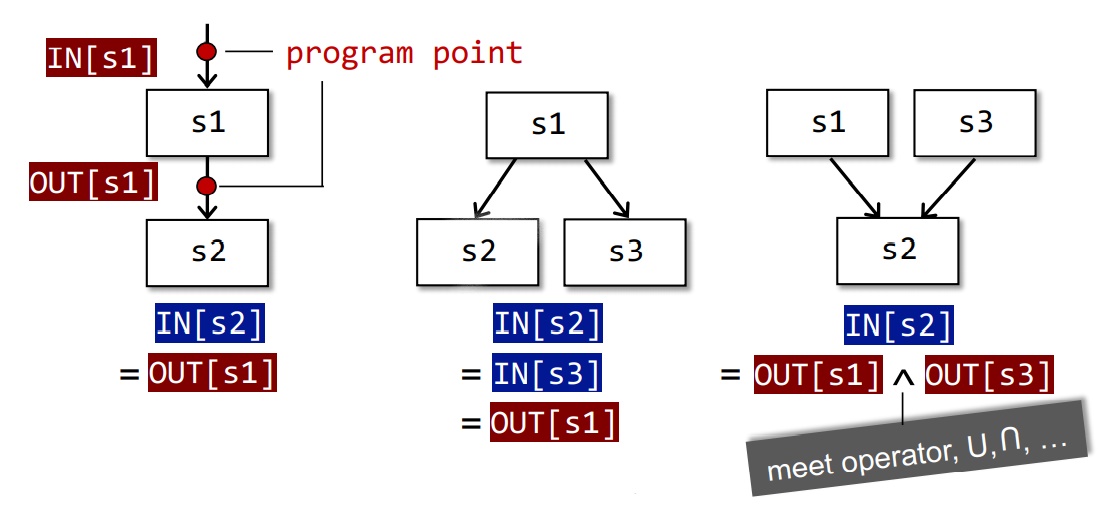
数据流方程是数据流分析中的核心概念，它描述了程序中数据的传播方式和处理机制。在形式化模型中，数据流方程通常表示为变量间的关系，定义了如何从程序的某些部分（如程序点或基本块）计算出其他部分的属性。这些属性可以是变量的定义和使用，也可以是更复杂的性质，如潜在的别名关系。

数据流方程可以分为两大类：前向数据流分析和后向数据流分析。前向分析是指从程序的开始到结束传播数据信息，而后向分析则相反。例如，在计算变量活跃性时，前向分析会找出在某个点之后变量是否会被用到，而后向分析则确定在该点之前变量是否被使用。

### 2.1.2 数据流分析算法的分类

数据流分析算法可以根据它们处理问题的方式被分类。最基本的分类是迭代算法和工作列表算法。迭代算法使用一系列的数据流方程来反复计算节点的属性，直到达到一个固定点，即后续迭代不再产生变化。工作列表算法使用一个队列（或工作列表）来存储待处理的节点，并在计算过程中更新这个队列。

除了这两种基本算法，还有一种是基于路径的分析方法，它考虑了程序的路径，通过分析程序的路径来确定数据的传播。该方法通常用于更精确的分析，例如别名分析，但计算复杂度较高。

## 2.2 数据流方程的求解方法

### 2.2.1 工作列表算法

工作列表算法通过维护一个待处理节点的列表来迭代解决问题。每个节点被处理一次，计算其数据流属性，然后将其影响传播到其邻居节点。如果邻居节点的属性发生变化，则它们也会被添加到工作列表中。这个过程一直持续，直到工作列表为空，这意味着所有的节点都被处理并且属性不再发生变化。

这种方法的优点在于它简单且直观，易于实现。然而，它的缺点是在处理大型程序时可能会有很多重复计算，导致效率不高。

#### 示例代码块

def work_list_algorithm(graph, initial_values):
    work_list = set(graph.nodes())
    in_out = {node: initial_values[node] for node in graph.nodes()}

    while work_list:
        node = work_list.pop()
        current_in, current_out = in_out[node]

        # Calculate new values for node using transfer functions
        new_in, new_out = calculate_new_values(node, current_in, current_out)

        # Update values if anything changed
        if new_in != current_in or new_out != current_out:
            in_out[node] = (new_in, new_out)
            # Add affected neighbors to work list
            for neighbor in graph.neighbors(node):
                work_list.add(neighbor)
    return in_out

def calculate_new_values(node, current_in, current_out):
    # Placeholder for data flow analysis logic
    # ... (implementation details)
    pass

### 2.2.2 迭代算法的收敛性分析

迭代算法的核心思想是反复地应用数据流方程，直到结果不再变化。这意味着算法的收敛性至关重要。收敛性分析关注的是算法是否能够找到一个稳定的数据流属性集，以及在什么条件下可以达到这个稳定状态。

迭代算法的收敛速度取决于程序的结构和数据流方程的性质。例如，单调数据流问题通常具有良好的收敛性质，因为随着迭代的进行，数据流属性会单调变化，最终达到稳定。

### 2.2.3 前向与后向数据流分析

前向和后向数据流分析是两种基本的数据流分析方向。前向分析从程序的起点开始，沿着控制流图向终点传播信息。而后向分析则相反，从终点向起点传播。

前向分析适用于分析变量的定义到达点，例如确定变量在何处不再被使用。后向分析则适合于分析变量的使用到达点，例如确定变量的定义来自何处。

#### 示例表格

| 类型 | 方向 | 应用示例 | 优点 | 缺点 |
| ----- | ------ | ------------------- | ---------------------- | ------------------- |
| 前向 | 从起点到终点 | 计算活跃变量 | 易于实现 | 可能无法精确计算到达定义 |
| 后向 | 从终点到起点 | 计算变量定义的范围 | 可以准确计算到达定义 | 需要反向的控制流信息 |

## 2.3 数据流分析的不变式和优化

### 2.3.1 不变量分析的理论框架

在数据流分析中，不变式指的是在程序执行过程中的某些点，始终保持不变的性质。理解并应用不变式对于设计高效的数据流分析算法至关重要。不变式可以是简单的，如一个循环中的不变条件，也可以是复杂的，如程序中数据的不变关系。

#### 示例代码块

def invariant_analysis(block):
    # Placeholder for invariant analysis logic
    # ... (implementation details)
    invariants = []
    # Analyze bloc