SVM与其他算法的对比分析：选择SVM的正确时机

# 1. 支持向量机（SVM）基础理论

## 1.1 SVM的定义与核心思想
支持向量机（Support Vector Machines, SVM）是一种常用的监督学习算法，主要用于分类和回归任务。其核心思想是通过找到最优超平面，实现分类的边界最大化。在高维空间中，超平面是一个分隔不同类别的线或者面，使得各类别之间间隔尽可能大，增强模型的泛化能力。

## 1.2 SVM的数学模型
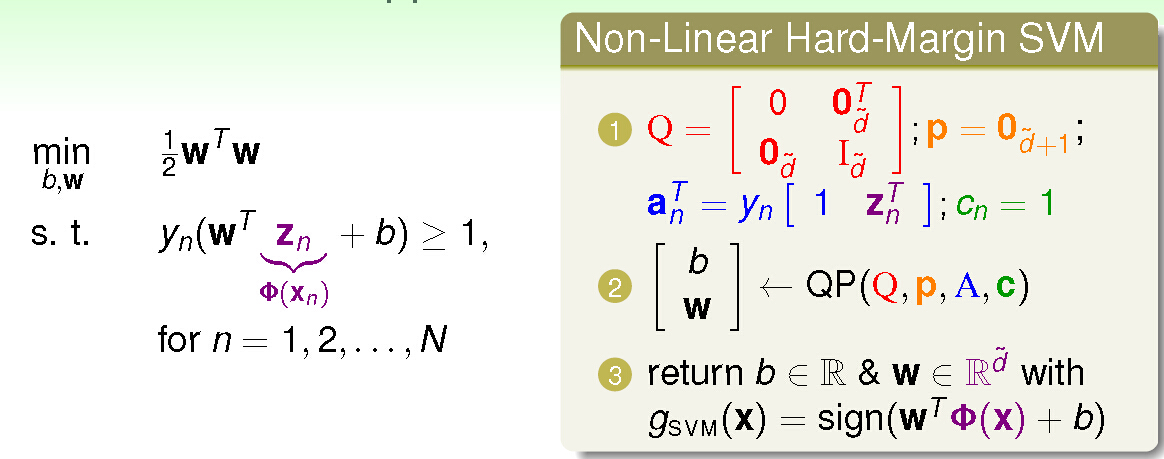
数学上，SVM模型的求解可以转化为一个二次规划问题。对于一个二分类问题，目标是找到一个分割超平面，使得各类数据点到该平面的距离最远。在实际应用中，为了处理线性不可分的情况，引入了软间隔的概念，并结合核技巧可以将数据映射到高维空间来解决非线性问题。

## 1.3 核技巧的应用
核技巧是SVM中的一个关键技术，它允许我们在原始特征空间上构造非线性决策边界，而不需要显式地在高维空间中进行计算。通过使用核函数（如多项式核、高斯径向基函数等），我们可以有效地计算出在高维空间中的点积，从而处理复杂的非线性分类问题。

# 2. SVM与其他分类算法的比较

SVM作为强大的分类算法，在与其他主流分类算法的对比中展现了其独特的性能和优势。本章节深入探讨SVM与决策树、K-最近邻算法（KNN）以及逻辑回归等常见算法的理论和实践差异。

## 2.1 常见分类算法概述

### 2.1.1 决策树

决策树是一种树形结构，它通过学习数据特征间的条件关系来进行预测。每个内部节点代表一个属性上的判断，分支代表判断结果，叶节点代表最终的分类结果。

#### 表格：决策树与其他算法的简单对比

| 特点 | 决策树 | SVM | KNN | 逻辑回归 |
| --- | --- | --- | --- | --- |
| 模型类型 | 基于规则的模型 | 基于核的模型 | 基于实例的模型 | 基于概率的模型 |
| 训练速度 | 较快 | 较慢 | 较慢 | 较快 |
| 泛化能力 | 中等 | 较强 | 较弱 | 中等 |
| 对噪声的敏感性 | 较强 | 较弱 | 中等 | 较强 |
| 处理高维数据的能力 | 弱 | 强 | 中等 | 中等 |

### 2.1.2 K-最近邻算法(KNN)

KNN是基于实例的学习方法，通过测量不同特征值之间的距离进行分类。在KNN中，数据点在特征空间中的位置越接近，它们就越可能是同一类别。

#### KNN算法实现代码示例：

from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

iris = load_iris()
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.5, random_state=42)

knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X_train, y_train)

#### 参数说明与逻辑分析：

- `KNeighborsClassifier`是用于创建KNN分类器的类。
- `n_neighbors`参数定义了用于选择k值，即最近邻的数量。
- `fit`函数用于训练模型，其中`X_train`和`y_train`分别是训练数据集的特征和标签。

### 2.1.3 逻辑回归

逻辑回归是一种广泛用于二分类问题的算法，通过应用sigmoid函数将线性回归的输出映射到(0,1)区间，形成概率。

#### 逻辑回归实现代码示例：

from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split

X, y = make_classification(n_samples=1000, n_features=20, n_informative=2, n_redundant=10, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=42)

logreg = LogisticRegression()
logreg.fit(X_train, y_train)

#### 参数说明与逻辑分析：

- `LogisticRegression`类是用于实现逻辑回归模型。
- `make_classification`函数用于生成模拟数据集，以便进行二分类问题的演示。
- `fit`函数同样用于训练模型，该函数接受特征集`X_train`和标签集`y_train`。

## 2.2 SVM与分类算法的理论对比

### 2.2.1 理论优势分析

SVM算法在理论上具有一定的优势，特别是其优化问题的求解为凸优化问题，有全局最优解。此外，SVM通过引入核函数，能够处理非线性问题，并具有良好的泛化能力。

### 2.2.2 理论局限性探讨

尽管SVM具备许多优势，但也有其局限性，比如对于高维数据的处理，它可能会受到所谓的“维数灾难”影响；此外，SVM模型参数的选取对于最终结果的影响很大，需要仔细调优。

## 2.3 SVM与其他算法的性能比较

### 2.3.1 实验设置和评价指标

本实验选择标准的UCI机器学习库数据集进行比较。评价指标包括准确率、召回率、F1分数以及计算效率。

### 2.3.2 实验结果分析

实验结果显示，SVM在大多数数据集上提供了最优的分类性能，尤其在非线性数据上表现突出。然而，在某些高维数据集上，SVM的训练时间显著增加。KNN在一些情况下提供了较好的结果，但其对大数据集的处理能力弱。逻辑回归则在简单问题上表现出色，但对于复杂问题，它的性能不如SVM。

在下一章节中，我们将讨论SVM在不同类型数据上的应用实践，包括线性可分数据和非线性数据集的处理方法，以及参数调优策略。

# 3. SVM在不同类型数据上的应用实践

## 3.1 线性可分数据集上的SVM应用

### 3.1.1 理论背景和线性核函数

支持向量机（SVM）在处理线性可分数据集时表现出色，其核心思想是寻找一个最优的超平面将不同类别的数据分隔开来，从而使得分割的边缘最大化。在线性可分的情况下，SVM寻求一个超平面，使得离该平面最近的异类样本之间的距离（称为边缘）最大化。这里，线性核函数起到关键作用，它保留了数据的线性结构，并通过点积运算在高维空间中寻找最优分割平面。

线性核函数是最简单的核函数形式，形式为 K(x, y) = <x, y>，其中x和y是两个向量，<x, y>表示它们的内积。线性核适合于原本就是线性可分的数据