SVM参数调优的艺术：网格搜索与贝叶斯优化的实用技巧

# 1. 支持向量机（SVM）简介

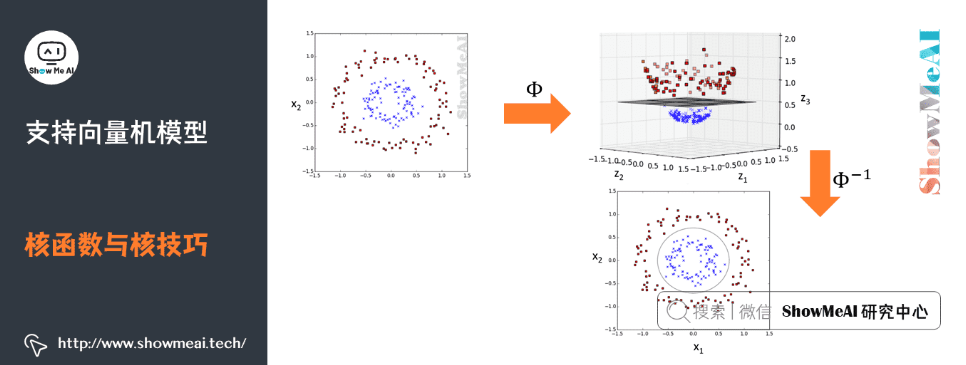
支持向量机（SVM）是一种强大的监督学习模型，广泛应用于分类和回归任务。它通过在特征空间中寻找最优的超平面来实现不同类别数据的划分，从而达到预测的目的。SVM的核心优势在于其独特的数学结构，特别是在高维空间中通过核技巧来处理非线性问题。在本章中，我们将简要介绍SVM的历史背景、基本原理以及它在机器学习中的重要性。通过了解SVM的基本概念，我们为后续深入探讨SVM的参数优化和调优方法打下基础。

# 2. SVM参数的重要性

## 2.1 SVM参数分类
SVM模型的性能很大程度上取决于其参数的选择，合理设置参数是保证模型表现的关键。SVM的参数可以大致分为三类：核函数参数、正则化参数、不敏感损失函数参数。

### 2.1.1 核函数参数
核函数的选择决定了数据在高维空间的表示方式。常见的核函数包括线性核、多项式核、径向基函数（RBF）核、sigmoid核等。核函数参数的调整主要影响模型的学习能力和泛化能力。

from sklearn.svm import SVC

# 设置不同核函数的SVM模型示例
svc_linear = SVC(kernel='linear')
svc_poly = SVC(kernel='poly', degree=3)
svc_rbf = SVC(kernel='rbf')
svc_sigmoid = SVC(kernel='sigmoid')

- `kernel='linear'`：选择线性核，适用于线性可分的数据集。
- `kernel='poly', degree=3`：选择多项式核，`degree`参数定义了多项式的次数，适用于非线性数据集。
- `kernel='rbf'`：选择RBF核，是一个普遍适用的核函数。
- `kernel='sigmoid'`：选择sigmoid核，有时能提供类似神经网络的效果。

### 2.1.2 正则化参数
正则化参数`C`控制了模型的复杂度和对错误分类的容忍度。较小的`C`值倾向于简单模型，可能会导致较大的分类间隔，但有可能造成欠拟合；较大的`C`值倾向于复杂模型，允许较小的分类间隔，但可能会导致过拟合。

# 设置不同正则化参数C的SVM模型示例
svc_C_small = SVC(kernel='rbf', C=0.1)
svc_C_large = SVC(kernel='rbf', C=100.0)

- `C=0.1`：较小的`C`值，倾向于简单模型，适用于数据集噪音较小的情况。
- `C=100.0`：较大的`C`值，倾向于复杂模型，适用于数据集噪音较大，对模型准确性要求较高的情况。

### 2.1.3 不敏感损失函数参数
对于SVM中的错误分类点，不敏感损失函数参数`epsilon`定义了一个间隔，允许该间隔内的数据点不被计为错误分类。较小的`epsilon`值意味着模型会尽量缩小间隔，提高模型对训练数据的拟合程度，可能导致过拟合；较大的`epsilon`值意味着模型会容忍较大的间隔，可能导致欠拟合。

# 设置不同不敏感损失函数参数epsilon的SVM模型示例
svc_epsilon_small = SVC(kernel='rbf', epsilon=0.01)
svc_epsilon_large = SVC(kernel='rbf', epsilon=1.0)

- `epsilon=0.01`：较小的`epsilon`值，模型对训练集的拟合度高，可能导致过拟合。
- `epsilon=1.0`：较大的`epsilon`值，模型对训练集的拟合度低，可能导致欠拟合。

## 2.2 参数对模型的影响

### 2.2.1 参数与模型复杂度
模型复杂度是指模型对训练数据的拟合能力。SVM模型的复杂度直接受核函数参数、正则化参数C和不敏感损失函数参数epsilon的影响。模型复杂度的增加会提高模型对训练数据的拟合能力，但同时也可能降低模型的泛化能力。

### 2.2.2 参数与模型泛化能力
泛化能力是指模型对未知数据的预测能力。理想的参数配置会平衡模型的复杂度和泛化能力，以达到最佳的预测表现。过高的复杂度可能导致模型对训练数据过拟合，而泛化能力下降；相反，过低的复杂度可能导致模型欠拟合，对训练数据的预测能力不足。因此，合理选择SVM的参数是保证模型泛化能力的关键。

graph LR
A[SVM参数配置] --> B[增加模型复杂度]
B --> C[提高模型对训练数据拟合能力]
C -->|过高| D[过拟合]
C -->|适当| E[理想泛化能力]
A --> F[降低模型复杂度]
F --> G[降低模型对训练数据拟合能力]
G -->|过低| H[欠拟合]
G -->|适当| I[理想泛化能力]

通过上述分析可知，SVM参数的配置需要权衡模型复杂度和泛化能力，找到二者的最佳平衡点，以确保模型在处理未知数据时能展现出最佳性能。在下一节中，我们将探讨通过网格搜索来实现SVM参数的调优，进一步深入了解如何在实践中寻找这些关键参数的最佳配置。

# 3. 网格搜索调优法

## 3.1 网格搜索基础

### 3.1.1 网格搜索工作原理

网格搜索是一种简单直观的参数优化方法，它通过尝试参数组合的每一个可能值来寻找最优的模型配置。它的工作原理类似于穷举法，创建一个参数值的“网格”，并在这个网格上遍历所有可能的参数组合。每次遍历都相当于对模型进行一次训练和验证，并记录下最优的参数组合。

### 3.1.2 网格搜索的实现步骤

在实际操作中，网格搜索的实现步骤可以分解如下：

1. 确定参数范围：首先，确定要优化的参数名称以及每个参数的候选值集合。
2. 创建参数网格：将参数及其候选值组合成一个网格结构，通常可以使用`sklearn.model_selection`模块中的`GridSearchCV`函数来实现。
3. 训练模型：使用网格中的每一组参数训练模型，并在验证集上进行验证，记录结果。
4. 选择最佳参数：在所有的参数组合中，选择验证集上表现最好的一组参数作为最终模型的配置。

以下是一个使用`GridSearchCV`的例子，展示了如何对SVM的参数进行网格搜索：

from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

# 加载数据集
iris = load_iris()
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2)

# 创建SVC模型
svc = SVC()

# 设置参数网格
param_grid = {
    'C': [0.1, 1, 10, 100], 
    'gamma': [1, 0.1, 0.01, 0.001], 
    'kernel': ['rbf']
}

# 实例化GridSearchCV
grid_search = GridSearchCV(svc, param_grid, refit=True, verbose=2, cv=5)

# 执行网格搜索
grid_search.fit(X_train, y_train)

# 输出最优参数
print("Best parameters found: ", grid_search.best_params_)

# 使用最优参数模型对测试集进行预测
best_model = grid_search.best_estimator_
predictions = best_model.predict(X_test)

在这个例子中，我们设置了SVM的正则化参数`C`、核函数参数`gamma`和核函数类型`kernel`，并使用5折交叉验证来评估每一组参数的性能。

## 3.2 网格搜索的高级应用

### 3.2.1 并行化网格搜索

当参数组合数量庞大时，网格搜索的计算开销会非常高。为了加速这个过程，可以利用并行计算技术。`GridSearchCV`在`n_jobs`参数中提供了并行化