R语言中的nnet包：5个技巧优化神经网络参数，提升模型性能

# 1. nnet包和神经网络简介

在数据科学领域，神经网络作为一种强大的机器学习算法，已经得到了广泛的应用和认可。本章节旨在为读者提供一个关于nnet包以及神经网络基础概念的概览。nnet包是R语言中一个著名的软件包，它提供了一个实现前馈神经网络的基本框架，特别适合用于分类和回归问题。

## 1.1 神经网络的起源与应用

神经网络的概念源于对人脑神经元的模仿，是构建机器学习模型的一种独特方式。它由相互连接的节点组成，这些节点称为神经元或节点。网络通过调整连接权重和偏置来学习和改进任务执行的准确性。神经网络在图像识别、语音处理、自然语言处理和复杂数据模式识别等众多领域都发挥了重要作用。

## 1.2 nnet包功能简介

R语言中的nnet包是处理神经网络模型的一个基础工具，它能够创建单层和多层前馈神经网络。使用该包，数据科学家们可以迅速搭建起用于分类和回归任务的神经网络模型。nnet包简单易用，适合初学者入门，同时因其灵活性，也得到了更高级用户的青睐。

# 示例代码：使用nnet包创建简单的神经网络模型
library(nnet)
# 假设已有数据集 iris 和目标变量 Species
# 创建一个简单的分类神经网络模型
nn_model <- nnet(Species ~ ., data = iris, size = 10, decay = 1e-4, maxit = 1000)

在上述代码中，我们使用了著名的鸢尾花数据集（iris），并指定了目标变量Species。参数`size`指定了隐藏层的神经元数量，`decay`是正则化参数，`maxit`定义了迭代次数。这个过程仅用几行代码就完成了一个神经网络模型的构建。

# 2. 优化神经网络参数的理论基础

### 2.1 理解神经网络参数

#### 2.1.1 参数的定义和重要性

在神经网络的语境中，参数通常指的是权重和偏置项。权重决定了输入对输出的影响程度，而偏置则调整了神经元激活的阈值。这些参数是神经网络学习的基础，它们的值决定了模型能够捕捉到的数据特征和模式。

参数的重要性体现在以下几个方面：

- **学习能力**：通过调整参数，神经网络能够从训练数据中学习到复杂的函数关系。
- **泛化能力**：合适的参数设置可以确保模型在未知数据上具有良好的预测表现，即泛化能力。
- **计算效率**：参数的适当初始化和调整可以减少训练时间，提高计算效率。

#### 2.1.2 常见参数类型及其作用

- **权重（Weight）**：连接相邻两层神经元的参数，每个连接都有一个权重值。权重越大，相应的输入对输出的影响越大。
- **偏置（Bias）**：每个神经元除了权重外还有一个偏置值，它调整神经元的激活阈值。
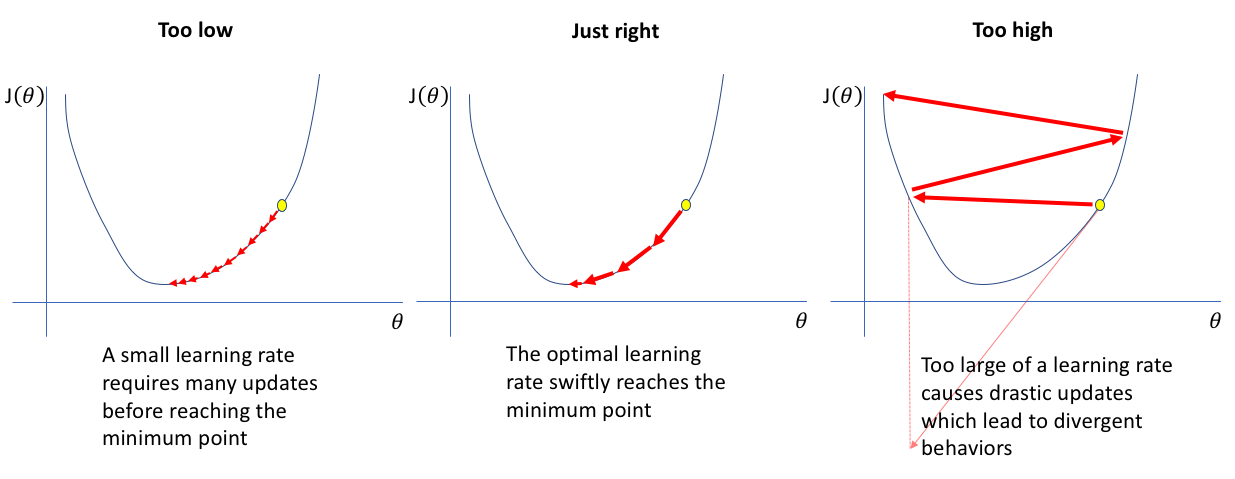
- **学习率（Learning Rate）**：控制权重更新速度的超参数，学习率的大小直接影响模型收敛的速度和质量。
- **激活函数参数**：某些激活函数（如Leaky ReLU）具有额外的参数，用于调节非线性变换的程度。

### 2.2 优化方法的选择

#### 2.2.1 优化算法对比

优化算法的选择对神经网络的训练效率和模型性能有着直接的影响。常见的优化算法包括随机梯度下降（SGD）、带动量的SGD（SGDM）、自适应学习率优化算法（如Adam和RMSprop）等。

- **随机梯度下降（SGD）**：通过迭代计算损失函数相对于每个参数的梯度来更新参数。优点是计算简单，但缺点是收敛速度可能较慢，且容易陷入局部最小值。
- **带动量的SGD（SGDM）**：在SGD的基础上加入了动量项，可以加速SGD在相关方向上的收敛，并抑制震荡。
- **Adam**：结合了动量和自适应学习率的概念，适合处理稀疏数据。

#### 2.2.2 理解局部最优与全局最优

在优化问题中，目标函数的全局最优解是所有可能解中具有最小（或最大）目标函数值的解，而局部最优解则是局部区域中的最优解。在多维参数空间中，神经网络优化问题可能会面临多个局部最优解，优化算法可能陷入其中而不继续探索更好的全局最优解。

因此，选择合适的优化算法和策略（如使用学习率衰减、梯度裁剪等技术）对于寻找全局最优解至关重要。

#### 2.2.3 交叉验证在参数优化中的应用

交叉验证是一种统计方法，用于评估并比较不同的参数设置。在神经网络中，可以通过交叉验证来优化模型的超参数，例如网络层数、隐藏单元数、学习率等。

常见的交叉验证方法有：

- **K折交叉验证**：将数据集分为K个大小相等的子集，其中K-1个子集用于训练，1个子集用于验证。这一过程重复K次，每次选择不同的验证集，最后计算K次评估结果的平均值。

交叉验证有助于减少模型对特定训练/验证集划分的依赖，从而更准确地评估模型的泛化能力。

### 2.3 优化参数的实践案例

在实践中，优化参数往往需要反复尝试和调整。以下是使用R语言进行参数优化的示例步骤：

# 安装并加载nnet包
install.packages("nnet")
library(nnet)

# 准备数据集
data(iris) # 使用iris数据集作为例子
X <- iris[, 1:4]  # 输入变量
Y <- as.factor(iris[, 5])  # 输出变量，这里用的是分类标签

# 创建训练集和测试集
set.seed(123)
train_index <- sample(seq_len(nrow(X)), size = 0.8 * nrow(X))
X_train <- X[train_index, ]
Y_train <- Y[train_index]
X_test <- X[-train_index, ]
Y_test <- Y[-train_index]

# 使用nnet函数训练神经网络模型
# 优化参数：大小为10的隐藏层，最大迭代次数为1000次，权重衰减因子为0.0001
nn_model <- nnet(Y_train ~ ., data = data.frame(Y_train, X_train), 
                 size = 10, maxit = 1000, decay = 0.0001)

# 使用训练好的模型进行预测
predictions <- predict(nn_model, newdata = data.frame(X_test), type = "class")

# 评估模型性能
table(predictions, Y_test)

此示例中，我们通过指定`size`（隐藏层神经元数量）、`maxit`（迭代次数）和`decay`（权重衰减因子）等参数来优化神经网络模型。实际应用中，我们可能还需要通过网格搜索、随机搜索或贝叶斯优化等方法来系统地探索超参数空间。

通过这一系列的理论基础和实际操作，我们可以更好地理解并应用神经网络参数优化的策略，以期达到提高模型性能的目的。

# 3. nnet包参数优化技巧

## 3.1 初始化权重和偏置

### 3.1.1 权重初始化方法

在使用nnet包进行神经网络模型的构建时，权重（weights）和偏置（biases）的初始化是一个关键步骤。合适的初始化方法可以提高网络的收敛速度，并且有助于避免训练过程中的梯度消失或爆炸问题。在实践中，有几种常见的权重初始化方法：

1. **零初始化**：将所有权重设置为0。这种方法简单，但会导致网络中所有神经元学习到相同的功能，因此不推荐用于非对称的神经网络。
2. **随机初始化**：权重从一个较小的随机分布中选择。这可以破坏对称性，帮助网络学习到更加多元化的特征。
3. **Xavier初始化（又名Glorot初始化）**：权重是根据网络层的输入和输出大小进行缩放的均匀分布或正态分布。Xavier初始化有助于保持信号在前向和反向传播过程中的方差一致，从而提高训练效率。
4. **He初始化**：是Xavier初始化的变体，特别为ReLU激活函数优化。权重初始化为`2 / fan_in`，其中`fan_in`是前一层神经元的数量。He初始化保持了方差在深层网络中的稳定。

### 3.1.2 偏置调整策略

与权重初始化类似，偏置的初始化也对模型的训练有着显著的影响。通常，偏置可以初始化为0，因为其不对称性问题不像权重那么敏感。在某些情况下，也可以给偏置一个较小的正数，比如0.01，以保证激活函数在开始时是活跃的。

### 3.1.3 示例代码：权重