控制到优化的综合策略：现代控制理论的应用详解


参考资源链接：[现代控制理论课后习题完整解答](https://wenku.csdn.net/doc/6412b5d2be7fbd1778d44848?spm=1055.2635.3001.10343)
# 1. 现代控制理论概述

现代控制理论是自动控制领域中的一门重要分支，它涉及对动态系统的建模、分析和设计。与传统控制理论相比，现代控制理论具有更为广泛的应用范围和更加严密的数学基础。本章将简要介绍现代控制理论的核心概念及其与传统控制理论的主要区别。

首先，现代控制理论的核心在于使用数学模型来描述控制系统的动态行为。这些数学模型通常包括微分方程、传递函数和状态空间模型等。通过这些模型，工程师可以对系统的响应进行精确预测和分析。

其次，现代控制理论强调系统性能指标的重要性，这些指标包括稳定性、响应速度、超调量等。为了满足这些性能要求，工程师会采用多种分析方法，比如根轨迹法和频率响应法，以确保控制系统的鲁棒性和可靠性。

最后，现代控制理论不仅仅局限于线性系统，它还广泛应用于非线性系统和多变量系统的控制，这使得它在复杂系统的控制策略设计和实现中发挥着不可或缺的作用。

# 2. 控制系统的建模与分析

在控制系统的设计与实施过程中，准确的建模与深入的分析是至关重要的。这不仅有助于我们理解系统的内在行为，而且还能为后续的控制策略设计提供坚实的基础。

## 2.1 系统的数学建模

数学建模是将实际物理系统转化为数学表达的过程。通过数学模型，我们可以预测系统在不同输入下的响应，并进行相应的分析与优化。

### 2.1.1 微分方程和传递函数

微分方程是描述系统动态行为的常用工具，而传递函数则是基于拉普拉斯变换的频域表示法。它们能够提供系统的输入输出关系。

**微分方程**：

考虑一个简单的弹簧质量阻尼系统，其动态可以描述为：

m\ddot{x}(t) + c\dot{x}(t) + kx(t) = f(t)

其中，`m`、`c`、`k`分别代表质量、阻尼和弹簧常数，`x(t)`是位移，`f(t)`是外力。

**传递函数**：

对于上述微分方程，我们可以通过拉普拉斯变换转换为传递函数的形式，系统传递函数为：

G(s) = \frac{X(s)}{F(s)} = \frac{1}{ms^2 + cs + k}

其中，`s`是拉普拉斯变换中的复变量，`X(s)`和`F(s)`分别是位移和外力的拉普拉斯变换。

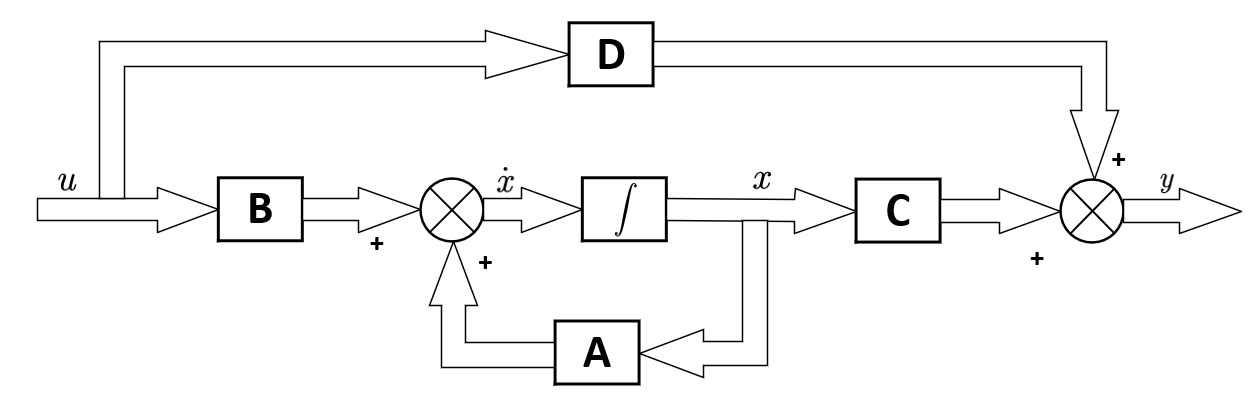
### 2.1.2 状态空间表示法

状态空间表示法为系统提供了一种更通用和灵活的建模方式，特别是在多变量和非线性系统的分析中显得尤为重要。

对于线性时不变系统，状态空间模型可以表示为：

\dot{x}(t) = Ax(t) + Bu(t) \\
y(t) = Cx(t) + Du(t)

其中，`x(t)`是状态向量，`u(t)`是输入向量，`y(t)`是输出向量，`A`、`B`、`C`、`D`是系统的状态空间矩阵。

**代码块示例**：

% 状态空间模型的MATLAB实现
A = [0 1; -k/m -c/m];
B = [0; 1/m];
C = [1 0];
D = [0];
sys = ss(A, B, C, D); % 创建状态空间模型

% 分析系统特性
eig(sys) % 计算系统的特征值

在这段代码中，首先定义了状态空间矩阵`A`、`B`、`C`和`D`，然后使用MATLAB的`ss`函数创建了状态空间模型`sys`。使用`eig(sys)`可以计算出系统矩阵`A`的特征值，这些特征值能够反映出系统的稳定性。

## 2.2 系统性能指标

性能指标是评价控制系统性能的量化标准。了解并掌握这些指标，对于设计一个高效可靠的控制系统至关重要。

### 2.2.1 稳定性

稳定性是控制系统最基本的要求。如果一个系统在受到扰动时能够返回到平衡状态，我们称这个系统是稳定的。

**稳定性分析**：

对于线性系统，稳定性可以基于系统的特征值进行判断：

- 如果所有特征值的实部都为负，则系统是稳定的。
- 如果至少有一个特征值的实部为正，则系统是不稳定的。

### 2.2.2 响应速度和超调量

响应速度和超调量是评价系统动态性能的两个重要指标。

- **响应速度**：指系统输出达到期望值变化的快慢。一般来说，响应速度越快，系统的性能越好。
- **超调量**：指系统输出在达到稳态值之前超过期望值的最大值。超调量越小，说明系统的过渡过程越平滑。

**代码块示例**：

% 分析系统的阶跃响应特性
figure
step(sys); % 绘制系统的阶跃响应图
title('Step Response')
grid on

% 读取响应数据，计算性能指标
[y,t] = step(sys);
overshoot = max(y) - 1; % 计算超调量
riseTime = t(100) - t(1); % 计算上升时间
settlingTime = t(900) - t(100); % 计算稳态时间

% 输出结果
fprintf('Overshoot: %.2f%%\n', overshoot * 100);
fprintf('Rise Time: %.2f s\n', riseTime);
fprintf('Settling Time: %.2f s\n', settlingTime);

在这段MATLAB代码中，我们使用`step`函数绘制了系统的阶跃响应，并计算了超调量、上升时间和稳态时间。这些数据帮助我们评价系统性能，并在设计控制器时进行优化。

## 2.3 系统分析方法

了解并掌握不同的系统分析方法，可以帮助我们从多个角度深入理解系统特性。

### 2.3.1 根轨迹法

根轨迹法是一种基于开环传递函数零极点变化来研究闭环系统稳定性的分析技术。

**根轨迹法的原理**：

- 根轨迹是闭环极点随开环增益变化的轨迹。
- 根轨迹的分支数等于系统的开环传递函数的极点数。
- 在根轨迹上，系统的动态性能和稳定性可以通过极点位置来评估。

**mermaid流程图示例**：

graph TD
    A[开始分析] --> B[确定开环传递函数]
    B --> C[计算开环极点和零点]
    C --> D[绘制根轨迹图]
    D --> E[分析闭环极点位置]
    E --> F[评估系统稳定性]
    F --> G[结束分析]

### 2.3.2 频率响应法

频率响应法通过分析系统对不同频率输入信号的响应来判断系统特性。

**频率响应法的原理**：

- 使用正弦波信号作为输入，测量系统输出与输入之间的幅度和相位差。
- 幅度比和相位差随频率变化的关系分别称为幅度频谱和相位频谱。
- 频率响应可以通过奈奎斯特图或波特图表示。

**表格示例**：

| 频率 (Hz) | 幅度比 (dB) | 相位差 (度) |
|-----------|-------------|-------------|
| 10 | -3.01 | -15 |
| 100 | -6.02 | -45 |
| 1000 | -9.03 | -75 |
| ... | ... | ... |

以上表格显示了在不同频率下系统的幅度比和相位差，有助于我们从频率响应的角度了解系统的稳定性和动态特性。

通过上述分析，我们可以对控制系统的建模与分析有了更深入的理解，这将为后续的控制策略设计奠定坚实的基础。

# 3. 控制策略的设计与实现

在现代控制系统中，设计与实现一个有效的控制策略至关重要，因为这直接关系到系统性能和稳定性。本章将详细探讨传统控制策略与智能控制策略，并分析如何通过仿真工具来实现和测试控制器。

## 3.1 传统控制策略
传统控制策略指的是那些已经存在多年且被广泛使用的控制技术。它们通常基于系统的数学模型来进行设计。本节将深入探讨比例-积分-微分（PID）控制和状态反馈控制。

### 3.1.1 比例-积分-微分（PID）控制
PID控制器是控制理论中最常见的一种反馈回路，它利用比例（P）、积分（I）、微分