系统稳定性与性能评估：现代控制理论的深入学习路径


参考资源链接：[现代控制理论课后习题完整解答](https://wenku.csdn.net/doc/6412b5d2be7fbd1778d44848?spm=1055.2635.3001.10343)
# 1. 系统稳定性与性能评估概述

## 1.1 评估的重要性与目的
在当今IT和自动化系统领域，系统稳定性与性能评估是确保服务质量（QoS）和技术产品可靠性的基石。此过程不仅涉及定量分析，还包括对系统运行时可能出现的问题进行预防性预测。对系统进行详尽的评估，可以揭示潜在的瓶颈，优化资源配置，提高系统的整体性能和用户的满意度。

## 1.2 系统稳定性与性能评估的基本方法
评估过程中通常会使用一系列指标和工具来度量系统的稳定性与性能。这些工具包括压力测试、负载测试、故障模拟等，它们可以帮助工程师从不同维度对系统的可靠性和响应能力进行测量。除了传统的工具，还可能包括各种数据分析技术，如时间序列分析、预测建模等，以便更准确地了解系统行为。

## 1.3 评估的实用意义与挑战
对系统进行稳定性与性能评估，有助于及时发现和解决潜在问题，减少系统故障带来的负面影响。然而，由于系统的多样性和复杂性，评估工作面临诸如数据采集困难、环境因素难以模拟、评估结果的解释与应用等挑战。因此，如何运用高效且精确的评估方法，以及如何整合和利用评估结果，是系统稳定性和性能评估工作中的关键问题。

# 2. 现代控制理论基础

现代控制理论是研究复杂系统动态行为的基础框架，为各种工业、科学和工程领域提供了解决问题的工具。通过建立数学模型来描述系统的行为，可以进行稳定性分析，进而设计出满足性能指标要求的控制器。控制系统的数学模型、稳定性分析和性能指标是现代控制理论的三大支柱。

### 控制系统的数学模型

#### 系统描述与状态空间表示

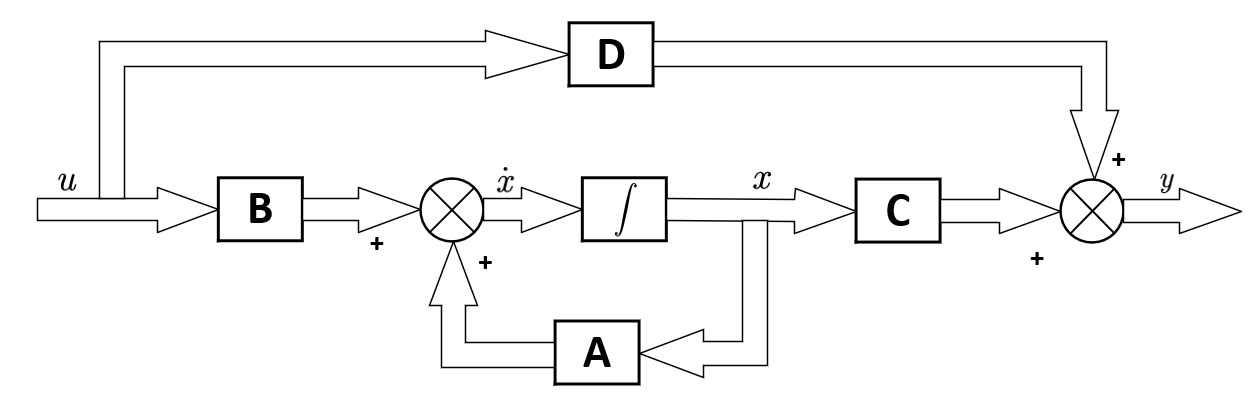
控制系统通常由一系列的数学模型来描述，这些模型能够体现系统内在的动态关系。状态空间模型因其能清晰描述系统状态变量的动态演变过程而受到广泛应用。在状态空间表示中，系统的动态行为由一系列一阶微分方程来描述：

\begin{align*}
\dot{x}(t) &= Ax(t) + Bu(t) \\
y(t) &= Cx(t) + Du(t)
\end{align*}

其中，\(x(t)\) 是状态向量，\(u(t)\) 是控制输入，\(y(t)\) 是输出向量，而矩阵 \(A, B, C, D\) 分别代表系统的内部动态、输入影响、输出关系和直接传递项。

#### 传递函数与拉普拉斯变换

传递函数是通过拉普拉斯变换将时间域中的微分方程转换成复频域中代数方程的一种表示方式。对于线性时不变系统（LTI系统），其传递函数 \(G(s)\) 可以表示为：

G(s) = \frac{Y(s)}{U(s)} = \frac{C(sI - A)^{-1}B + D}{sI - A}

其中，\(Y(s)\) 和 \(U(s)\) 分别是输出 \(y(t)\) 和输入 \(u(t)\) 的拉普拉斯变换。这种表示法简化了系统的分析，特别是在系统稳定性分析和设计反馈控制器时。

### 系统稳定性分析

#### 李雅普诺夫稳定性理论

系统的稳定性是控制系统设计中的核心问题。李雅普诺夫稳定性理论提供了一种非线性系统稳定性的判定方法。一个系统在平衡点的稳定性可以通过找到一个李雅普诺夫函数 \(V(x)\)，它是一个正定函数，其导数满足：

\frac{dV}{dt} < 0

如果这样的函数可以找到，则可以判定系统在平衡点是渐进稳定的。

#### 鲁棒性与稳定边界分析

在现实世界中，系统通常受到未知干扰和参数变化的影响。鲁棒性意味着系统能在一定范围内的参数变化和干扰下保持其性能。分析系统的稳定边界可以确定系统可以容忍的参数变化范围，这对于设计出在各种环境下都可靠的控制系统至关重要。

### 系统性能指标

#### 响应速度与阻尼比

控制系统的性能指标是衡量系统性能的关键参数。响应速度是指系统对输入变化的反应快慢，阻尼比则是衡量振荡系统振荡衰减速度的指标。理想情况下，设计的系统应具备快速响应速度与适当的阻尼比，以确保系统既能迅速达到稳定状态，又能避免过度振荡。

#### 过渡过程与稳态误差评估

系统达到稳定状态后，其输出可能会在期望值周围波动，这种现象称为过渡过程。过渡过程中的误差称为过渡误差，其评估对于确保系统最终输出的准确性至关重要。稳态误差评估则关注系统在长时间运行后，输出与期望值之间的误差大小。

在设计控制系统时，工程师会使用各种工具和方法来优化这些性能指标，以满足具体应用的需要。下一章节，我们将探讨控制理论在实践中的应用，并通过实际案例分析展示其实际效果。

# 3. 控制理论的实践应用

## 3.1 控制系统的设计方法

### 3.1.1 PID控制器设计与调整

比例-积分-微分（PID）控制是最常用的控制策略之一，它通过结合比例（P）、积分（I）和微分（D）三个动作，对系统进行精确控制。设计PID控制器的关键在于选取适当的参数，这通常通过经验规则、试错或优化算法实现。

#### 设计步骤

1. **设定系统目标**：首先确定控制系统的性能指标，如超调量、上升时间、稳态误差等。
2. **选择控制模式**：根据控制对象和控制目标选择合适的控制模式，例如位置式PID或增量式PID。
3. **参数整定**：使用如Ziegler-Nichols方法等来确定P、I、D三个参数的初值，然后通过调整试验找到最佳参数。
4. **测试与优化**：在仿真或实际环境中测试PID控制器的性能，并根据需要进行微调。

#### 代码示例

import numpy as np
import matplotlib.pyplot as plt

# 设定PID参数
Kp = 1.0
Ki = 0.1
Kd = 0.05

# 设定一个简单的一阶系统模型
def system_output(t, setpoint, Kp, Ki, Kd):
    # 系统响应函数（示例）
    return setpoint * (1 - np.exp(-Kp * t))

# 模拟PID控制下的系统响应
time = np.linspace(0, 10, 100)
setpoint = 1.0
response = [system_output(t, setpoint, Kp, Ki, Kd) for t in time]

# 绘图
plt.plot(time, response)
plt.xlabel('Time')
plt.ylabel('System Response')
plt.title('PID Control Response')
plt.show()

在以上代码中，我们模拟了一个简单的一阶系统响应。实际应用中需要将系统模型替换为实际系统，并根据系统的反馈信号调整PID参数，以达到期望的控制效果。

### 3.1.2 状态反馈与观测器设计

状态反馈控制器的设计涉及系统状态的测量或估计。在实际中，不是所有的状态变量都是可测量的。因此，设计观测器来估计这些不可测状态变得非常关键。

#### 状态反馈控制

- 状态反馈控制通常基于系统的状态空间模型。
- 利用状态观测器（如卡尔曼滤波器）获取系统状态。
- 设计控制律，使得系统输出跟踪期望参考轨迹。

#### 观测器设计

- 观测器的目的是估计