因果图：IT故障诊断的权威指南，从理论到实践

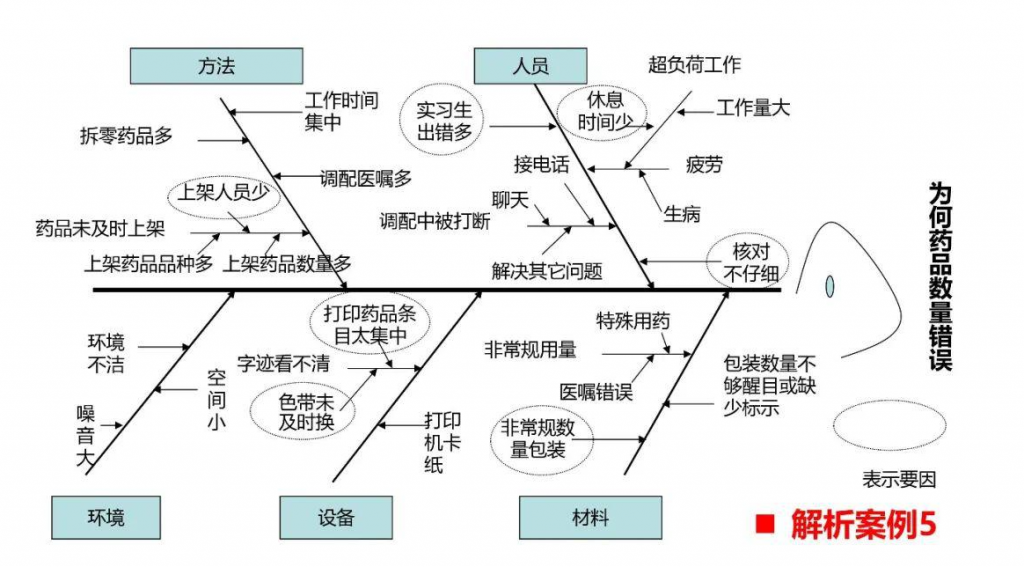
# 1. 因果图基础**

因果图是一种可视化工具，用于表示和分析复杂系统中的因果关系。它通过节点和箭头来表示变量及其相互作用，有助于理解系统行为并识别潜在的影响因素。

因果图由以下元素组成：

- **节点：**表示系统中的变量或因素。
- **箭头：**表示变量之间的因果关系。箭头方向指向因变量（受影响的变量）。
- **符号：**用于表示因果关系的类型，例如正相关（+）或负相关（-）。

# 2. 因果图理论

### 2.1 因果关系的建模

#### 2.1.1 因果图的元素和符号

因果图是一种可视化工具，用于表示变量之间的因果关系。它由以下元素组成：

* **变量：**因果图中的变量用圆圈表示，代表系统中感兴趣的因素。
* **箭头：**箭头连接变量，表示因果关系。箭头指向的变量是因变量，箭头发出的变量是自变量。
* **箭头类型：**箭头可以是实线或虚线。实线表示确定的因果关系，虚线表示不确定的因果关系。
* **节点类型：**变量节点可以是观测节点或潜在节点。观测节点表示可直接观测到的变量，潜在节点表示不可直接观测到的变量。

#### 2.1.2 因果图的构建原则

构建因果图时，应遵循以下原则：

* **明确因果关系：**箭头应准确反映变量之间的因果关系，避免循环或自反馈回路。
* **考虑相关性：**相关性不等于因果关系。构建因果图时，应考虑变量之间的相关性，但不能将相关性误认为因果关系。
* **使用领域知识：**因果图应基于对系统或领域的理解。利用领域知识可以帮助识别变量之间的因果关系。
* **保持简洁性：**因果图应简洁明了，只包含与分析相关的变量和关系。

### 2.2 因果关系的分析

#### 2.2.1 概率推理

概率推理是使用因果图推断变量概率的方法。它基于以下原理：

* **条件概率：**一个变量的概率可以通过给定其他变量的条件概率来计算。
* **贝叶斯定理：**贝叶斯定理提供了一种计算条件概率的方法。

通过使用概率推理，我们可以从因果图中推断变量的概率分布。这对于识别故障原因和预测系统行为至关重要。

#### 2.2.2 敏感性分析

敏感性分析是一种评估变量变化对因果图结果影响的方法。它涉及以下步骤：

1. **改变变量值：**改变一个或多个变量的值。
2. **重新计算概率：**使用概率推理重新计算因果图中变量的概率分布。
3. **比较结果：**比较改变变量值前后概率分布的变化。

敏感性分析可以帮助我们识别对系统行为影响最大的变量，并确定哪些变量需要密切监控。

# 导入因果图库
import py因果图

# 创建因果图
graph = py因果图.DAG()

# 添加变量
graph.add_nodes_from(['A', 'B', 'C', 'D'])

# 添加因果关系
graph.add_edges_from([('A', 'B'), ('B', 'C'), ('C', 'D')])

# 设置条件概率
graph.set_cpds({'A': ['0.5'], 'B': ['0.3', '0.7'], 'C': ['0.2', '0.8'], 'D': ['0.1', '0.9']})

# 概率推理
p_d_given_a = graph.query('P(D | A=True)')
print(p_d_given_a)

# 敏感性分析
graph.set_cpd('A', ['0.8'])
p_d_given_a_new = graph.query('P(D | A=True)')
print(p_d_given_a_new)

**代码逻辑分析：**

* 第 1 行：导入因果图库。
* 第 3-6 行：创建因果图，添加变量和因果关系。
* 第 8-11 行：设置条件概率。
* 第 13 行：使用概率推理计算变量 D 在给定变量 A 为 True 时的概率。
* 第 16 行：修改变量 A 的条件概率。
* 第 18 行：重新计算变量 D 在给定变量 A 为 True 时的概率。

**参数说明：**

* `graph.add_nodes_from()`：添加变量到因果图。
* `graph.add_edges_from()`：添加因果关系到因果图。
* `graph.set_cpds()`：设置变量的条件概率分布。
* `graph.query()`：使用概率推理计算变量的概率分布。

# 3. 因果图实践**

**3.1 IT故障诊断中的因果图应用**

因果图在IT故障诊断中发挥着至关重要的作用，它可以帮助故障分析人员快速识别和分析故障原因，从而提高故障诊断的效率和准确性。

**3.1.1 故障场景的因果图建模**

构建故障场景的因果图时，需要遵循以下原则：

- **明确故障目标：**明确需要诊断的故障现象或问题。
- **识别潜在原因：**通过头脑风暴、经验积累或知识库，列出所有可能导致故障的潜在原因。
- **建立因果关系：**分析潜在原因之间的逻辑关系，确定它们之间的因果关系。
- **绘制因果图：**使用因果图符号（如节点、箭头、圆圈等）绘制因果图，表示原因之间的关系。

**3.1.2 故障原因的识别和分析**

构建因果图后，就可以进行故障原因的识别和分析：

- **概率推理：**通过因果图的概率推理，计算每个潜在原因导致故障的概率。
- **敏感性分析：**通过改变因果图中某些原因的概率，分析其对故障概率的影响，从而识别关键原因。
- **故障树分析：**将因果图转换为故障树，进一步分析故障发生的逻辑路径和概率。

**3.2 因果图在IT运维中的应用**

除了故障诊断，因果图在IT运维的其他方面也有广泛的应用：

**3.2.1 故障预防和风险评估**

- **识别潜在风险：**通过因果图分析，识别可能导致故障的潜在风险因素。
- **评估风险概率：**计算每个风险因素导致故障的概率，评估故障发生的可能性。
- **制定预防措施：**根据风险评估结果，制定预防措施，降低故障发生的概率。

**3.2.2 故障管理和优化**

- **故障管理流程优化：**通过因果图分析故障管理流程，识别瓶颈和优化点，提高故障处理效率。
- **故障根因分析：**使用因果图深入分析故障根因，避免故障重复发生。
- **故障知识库构建：**将因果图作为故障知识库的一部分，积累和共享故障分析经验。

**代码示例：**

# 故障场景因果图建模
import networkx as nx

# 创建因果图
graph = nx.DiGraph()
graph.add_nodes_from(["故障现象", "原因1", "原因2", "原因3"])
graph.add_edges_from([("原因1", "故障现象"), ("原因2", "故障现象"), ("原因3", "故障现象")])

# 概率推理
nx.set_node_attributes(graph, {"probability": {"故障现象": 0.5, "原因1": 0.2, "原因2": 0.3, "原因3": 0.1}})
nx.pagerank(graph)

# 敏感性分析
for node in graph.nodes():
    graph.nodes[node]["probability"] += 0.1
    print(nx.pagerank(graph)[node])

**逻辑分析：**

代码示例演示了如何使用NetworkX库构建故障场景的因果图并进行概率推理和敏感性分析。通过修改原因节点的概率，我们可以分析其对故障概率的影响，从而识别关键原因。

# 4. 因果图进阶

### 4.1 因果图的扩展

#### 4.1.1 动态因果图

传统的因果图是静态的，无法描述系统随时间变化的因果关系。动态因果图（Dynamic Bayesian Networks，DBN）通过引入时间维度，可以对动态系统进行建模。DBN由一系列时间切片组成，每个时间切片是一个因果图，描述了系统在该时间点的状态。相邻时间切片之间的连接表示了系统状态随时间的演变。

**代码块：**

import pgmpy
from pgmpy.models import DynamicBayesianNetwork

# 创建一个简单的 DBN 模型
model = DynamicBayesianNetwork()
model.add_nodes_from(['A', 'B', 'C'])
model.add_edges_from([('A', 'B'), ('B', 'C')])
model.add_time_slice(['A', 'B'], time_slice=0)
model.add_time_slice(['B', 'C'], time_slice=1)

**逻辑分析：**

该代码创建了一个简单的 DBN 模型，其中节点 `A` 和 `B` 属于时间切片 0，节点 `B` 和 `C` 属于时间切片 1。

#### 4.1.2 多层因果图

多层因果图（Hierarchical Bayesian Networks，HBN）是一种分层结构的因果图，可以将复杂系统分解为多个子系统。HBN由多个层组成，每层表示系统的一个抽象级别。高层因果图描述了系统的高级结构，而低层因果图提供了更详细的信息。

**代码块：**

import pgmpy
from pgmpy.models import HierarchicalBayesianNetwork

# 创建一个简单的 HBN 模型
model = HierarchicalBayesianNetwork()
model.add_nodes_from(['A', 'B', 'C', 'D'])
model.add_edges_from([('A', 'B'), ('B', 'C'), ('C', 'D')])
model.add_submodel('submodel_1', ['A', 'B'])
model.add_submodel('submodel_2', ['C', 'D'])

**逻辑分析：**

该代码创建了一个简单的 HBN 模型，其中 `submodel_1` 包含节点 `A` 和 `B`，`submodel_2` 包含节点 `C` 和 `D`。

### 4.2 因果图与其他诊断方法的结合

#### 4.2.1 因果图与故障树分析

故障树分析（FTA）是一种自上而下的故障分析方法，从系统故障开始，逐步分解故障原因。因果图可以与 FTA 结合使用，以提高故障分析的准确性和效率。因果图可以提供故障原因之间的因果关系，而 FTA 可以帮助识别潜在的故障路径。

#### 4.2.2 因果图与贝叶斯网络

贝叶斯网络是一种概率图形模型，可以表示变量之间的概率依赖关系。因果图与贝叶斯网络可以结合使用，以进行概率推理和敏感性分析。因果图提供因果关系结构，而贝叶斯网络提供概率信息。

**表格：**

| 方法 | 优点 | 缺点 |
|---|---|---|
| 因果图 | 直观、易于理解 | 缺乏概率信息 |
| 故障树分析 | 系统性、全面 | 复杂性高 |
| 贝叶斯网络 | 概率推理、敏感性分析 | 依赖于先验概率 |

**流程图：**

[mermaid]
graph LR
subgraph 因果图
A[因果关系] --> B[故障原因]
end
subgraph 故障树分析
C[系统故障] --> D[故障原因 1]
C --> E[故障原因 2]
end
subgraph 贝叶斯网络
F[变量 1] --> G[变量 2]
F --> H[变量 3]
end
因果图 --> 故障树分析
因果图 --> 贝叶斯网络

# 5. 因果图工具和资源

### 5.1 因果图建模工具

**免费开源工具：**

- **CausalNex:** Python 库，用于因果图建模和分析。
- **DAGitty:** Web 应用，用于创建和编辑因果图。
- **GeNIe:** Java 库，用于因果图推理和可视化。

**商业工具：**

- **Netica:** 因果图建模和推理软件，提供高级分析功能。
- **Hugin:** 因果图建模和推理平台，具有协作和版本控制功能。
- **BayesiaLab:** 因果图建模和推理工具，专注于医疗领域。

### 5.2 因果图分析资源

**在线平台：**

- **CausalAI:** 提供因果图建模和分析教程、案例研究和资源。
- **MIT OpenCourseWare:** 提供因果推理和因果图建模的在线课程。
- **Coursera:** 提供因果推理和因果图建模的在线专业化课程。

**书籍：**

- **Causality: Models, Reasoning, and Inference:** Judea Pearl 著，因果推理的权威著作。
- **Causal Inference in Statistics: A Primer:** Judea Pearl、Madelyn Glymour 和 Nicholas Jewell 著，因果推理在统计学中的应用指南。
- **Bayesian Networks and Causal Inference:** Judea Pearl 著，因果推理和贝叶斯网络的综合介绍。

### 5.3 因果图最佳实践

**建模最佳实践：**

- 使用明确的符号和约定。
- 确保因果关系的准确性和完整性。
- 考虑潜在的混杂因素和偏见。

**分析最佳实践：**

- 使用概率推理来量化因果关系。
- 进行敏感性分析以评估结果的稳健性。
- 结合其他诊断方法以获得更全面的见解。