MATLAB稀疏矩阵并行化实战指南：提升稀疏矩阵计算速度的利器

# 1. 稀疏矩阵基础**

稀疏矩阵是一种特殊的矩阵，其中大部分元素为零。这种特性使得稀疏矩阵在存储和计算方面具有显著的优势。稀疏矩阵通常用于表示大型、复杂的数据集，例如科学计算、机器学习和数据挖掘中的数据。

稀疏矩阵的存储格式主要有两种：压缩行存储（CSR）和压缩列存储（CSC）。CSR格式将每一行的非零元素存储在一个一维数组中，并通过另一个一维数组记录每一行的起始位置。CSC格式类似，但将每一列的非零元素存储在一个一维数组中。

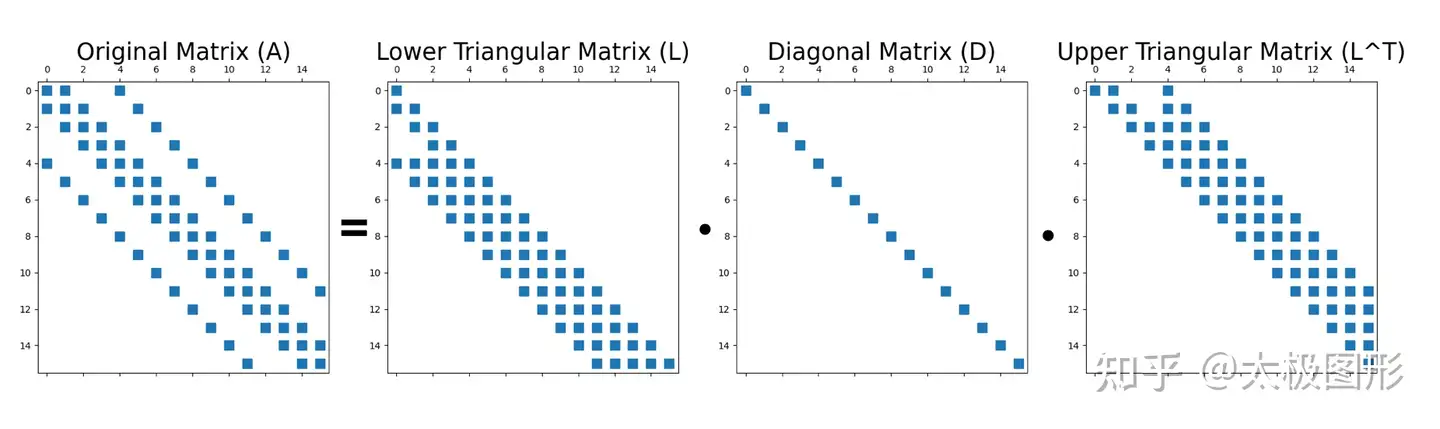
稀疏矩阵的运算主要包括稀疏矩阵-向量乘法、稀疏矩阵分解和稀疏矩阵求逆。稀疏矩阵-向量乘法是稀疏矩阵运算中最基本的操作，其计算复杂度为O(nnz)，其中nnz表示稀疏矩阵中非零元素的个数。稀疏矩阵分解是将稀疏矩阵分解为多个矩阵的乘积，用于求解线性方程组和特征值问题。稀疏矩阵求逆是计算稀疏矩阵的逆矩阵，其计算复杂度通常较高。

# 2. MATLAB稀疏矩阵并行化理论

### 2.1 并行计算基础

#### 2.1.1 并行计算模型

并行计算是一种通过同时使用多个计算资源（如处理器或计算机）来解决问题的计算范式。它通过将问题分解成较小的子任务，然后在多个资源上同时执行这些子任务来实现。常见的并行计算模型包括：

- **共享内存模型：**所有计算资源共享一个公共内存空间，可以同时访问和修改数据。
- **分布式内存模型：**每个计算资源拥有自己的私有内存空间，只能通过消息传递进行通信。

#### 2.1.2 并行编程范式

并行编程范式是用于组织和协调并行程序的抽象框架。常见的并行编程范式包括：

- **多进程编程：**创建多个独立的进程，每个进程都有自己的内存空间和执行线程。
- **多线程编程：**在一个进程内创建多个线程，这些线程共享相同的内存空间，但有自己的执行流。
- **消息传递编程：**使用显式消息传递机制在不同计算资源之间通信。

### 2.2 MATLAB并行计算工具箱

MATLAB提供了丰富的并行计算工具箱，简化了并行程序的开发和部署。

#### 2.2.1 并行池和并行计算器

**并行池**是管理并行计算资源的集合。它允许用户指定可用于并行计算的处理器数量和类型。

**并行计算器**是一个用于管理并行计算作业的高级对象。它提供了对并行池的访问，并允许用户提交和管理并行任务。

#### 2.2.2 并行化数组和数据结构

MATLAB支持对数组和数据结构进行并行化，从而提高数据处理和计算效率。

- **并行数组：**使用`pararray`函数创建，可以将数据分布到多个计算资源上，从而实现并行计算。
- **并行数据结构：**使用`parallel.pool.DataQueue`和`parallel.pool.DataExchange`等类创建，可以实现数据结构在并行计算器之间的高效通信和交换。

# 3. 稀疏矩阵并行化实践

### 3.1 并行稀疏矩阵-向量乘法

稀疏矩阵-向量乘法是稀疏矩阵计算中的基本操作，其并行化可以显著提高计算效率。MATLAB提供了两种并行稀疏矩阵-向量乘法算法：分块并行算法和循环并行算法。

#### 3.1.1 分块并行算法

分块并行算法将稀疏矩阵划分为多个块，每个块分配给不同的处理器并行计算。该算法的并行度取决于稀疏矩阵的块大小和处理器数量。

% 创建稀疏矩阵
A = sparse(rand(1000, 1000));

% 创建并行