剖析MATLAB稀疏矩阵存储格式：CSR、CSC、LIL的优劣势

# 1. MATLAB稀疏矩阵概述

稀疏矩阵是一种特殊的矩阵，其中大部分元素为零。在科学计算和数据分析中，稀疏矩阵非常常见，例如图论、有限元分析和机器学习。MATLAB提供了丰富的函数和工具，用于创建、操作和存储稀疏矩阵。

稀疏矩阵的存储格式对于性能至关重要。MATLAB支持多种稀疏矩阵存储格式，包括CSR（压缩行存储）、CSC（压缩列存储）和LIL（链接列表）。这些格式在存储空间、计算效率和灵活性方面各有优劣。

# 2. 理论基础

### 2.1 稀疏矩阵的概念和特点

稀疏矩阵是一种特殊的矩阵，其中大部分元素为零。与稠密矩阵相比，稀疏矩阵具有以下特点：

* **非零元素稀少：**非零元素的数量远小于矩阵的总元素数。
* **元素分布不均匀：**非零元素通常集中在矩阵的某些区域，而其他区域则为零。
* **存储空间需求低：**由于大部分元素为零，稀疏矩阵可以比稠密矩阵节省大量的存储空间。
* **计算效率高：**对于稀疏矩阵的许多操作（例如乘法、求逆），可以利用其稀疏性来优化算法，从而提高计算效率。

### 2.2 稀疏矩阵的存储格式：CSR、CSC、LIL

为了高效地存储和处理稀疏矩阵，需要使用专门的存储格式。最常用的稀疏矩阵存储格式包括：

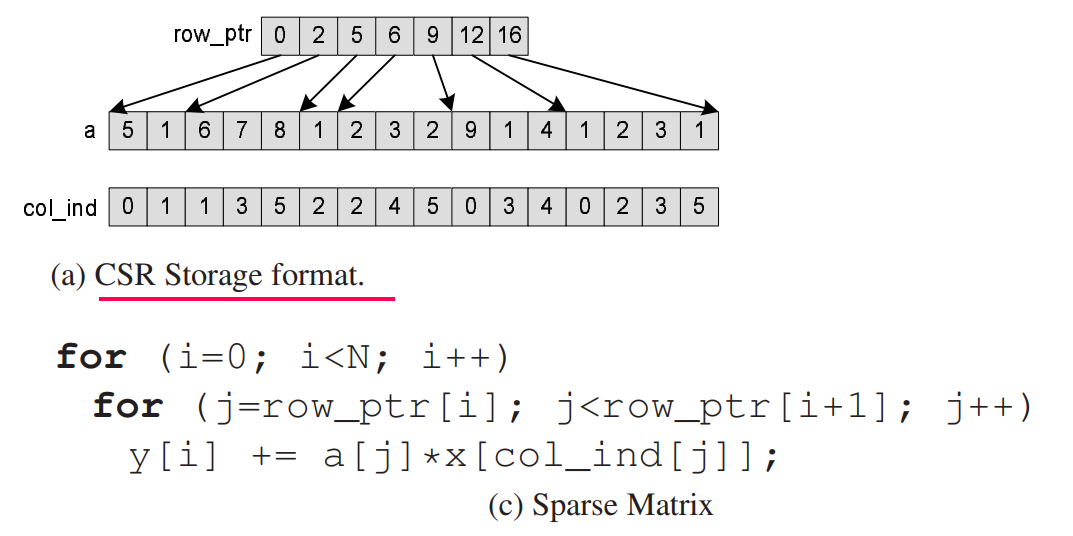
**CSR（Compressed Sparse Row）格式：**

CSR格式使用三个数组来存储稀疏矩阵：

* **行指针数组 (row_ptr)：**存储每一行的第一个非零元素在值数组中的索引。
* **列索引数组 (col_idx)：**存储所有非零元素的列索引。
* **值数组 (values)：**存储所有非零元素的值。

**CSC（Compressed Sparse Column）格式：**

CSC格式与CSR格式类似，但它是按列而不是按行存储的。它使用三个数组：

* **列指针数组 (col_ptr)：**存储每一列的第一个非零元素在值数组中的索引。
* **行索引数组 (row_idx)：**存储所有非零元素的行索引。
* **值数组 (values)：**存储所有非零元素的值。

**LIL（Linked List）格式：**

LIL格式使用一个链表来存储稀疏矩阵。对于每一行，它创建一个链表，其中每个节点存储一个非零元素及其列索引。

**代码块：**

import numpy as np

# 创建一个稀疏矩阵
A = np.array([[1, 0, 0], [0, 2, 0], [0, 0, 3]])

# 将稀疏矩阵转换为CSR格式
csr_A = A.tocsr()

# 访问CSR格式稀疏矩阵的元素
print(csr_A.data)  # 非零元素的值
print(csr_A.indices)  # 非零元素的列索引
print(csr_A.indptr)  # 行指针数组

**逻辑分析：**

* `tocsr()`方法将稠密矩阵转换为CSR格式稀疏矩阵。
* `data`属性存储非零元素的值。
* `indices`属性存储非零元素的列索引。
* `indptr`属性存储行指针数组。

**参数说明：**

* `A`：要转换的稠密矩阵。
* `data`：非零元素的值。
* `indices`：非零元素的列索引。
* `indptr`：行指针数组。

# 3. CSC、LIL存储格式的优劣势：实践比较

### 3.1 CSR、CSC、LIL存储格式的原理和实现

**CSR（Compressed Sparse Row）格式**

CSR格式是一种按行存储稀疏矩阵的格式。它由三个数组组成：

- `val`：存储非零元素的值。
- `col_ind`：存储非零元素所在列的索引。
- `row_ptr`：存储每一行非零元素在`val`和`col_ind`数组中的起始位置。

**CSC（Compressed Sparse Column）格式**

CSC格式是一种按列存储稀疏矩阵的格式。它由三个数组组成：

- `val`：存储非零元素的值。
- `row_ind`：存储非零元素所在行的索引。
- `col_ptr`：存储每一列非零元素在`val`和`row_ind`数组中的起始位置。

**LIL（Linked List）格式**

LIL格式是一种使用链表存储稀疏矩阵的格式。它由两个数组组成：

- `val`：存储非零元素的值。
- `rows`：存储非零元素所在行的链表。每个链表节点包含一个指向下一行的指针和一个存储列索引的字段。

### 3.2 CSR、CSC、LIL存储格式的优劣势分析

| 存储格式 | 优点 | 缺点 |
|---|---|---|
| CSR | 访问行数据高效 | 访问列数据效率低 |
| CSC | 访问列数据高效 | 访问行数据效率低 |
| LIL | 灵活，易于修改 | 存储空间开销大 |

**CSR格式**

* 优点：
* 访问行数据高效，因为行数据是连续存储的。
* 存储空间开销小，因为只存储非零元素。
* 缺点：
* 访问列数据效率低，因为列数据是分散存储的。

**CSC格式**

* 优点：
* 访问列数据高效，因为列数据是连续存储的。
* 存储空间开销小，因为只存储非零元素。
* 缺点：
* 访问行数据效率低，因为行数据是分散存储的。

**LIL格式**

* 优点：
* 灵活，易于修改，因为使用链表存储非零元素。
* 缺点：
* 存储空间开销大，因为需要存储链表节点。

### 3.3 不同稀疏矩阵类型下的存储格式选择

选择合适的稀疏矩阵存储格式取决于矩阵的特性和应用程序的需求。

* 如果需要频繁访问行数据，则CSR格式是最佳选择。
* 如果需要频繁访问列数据，则CSC格式是最佳选择。
* 如果需要频繁修改矩阵，则LIL格式是最佳选择。

**示例：**

考虑一个稀疏矩阵，其中行数远大于列数。在这种情况下，使用CSR格式将更有效，因为它可以高效地访问行数据。

import numpy as np

# 创建一个稀疏矩阵
A = np.array([[1, 0, 0], [0, 2, 0], [0, 0, 3]])

# 转换为CSR格式
csr_A = A.tocsr()

# 访问行数据
print(csr_A.getrow(0))

# 访问列数据
print(csr_A.getcol(1))

**输出：**

[1. 0. 0.]
[0. 2. 0.]

# 4.1 图论中的稀疏矩阵应用

### 图论简介

图论是数学的一个分支，它研究由顶点和边组成的结构。图论在计算机科学中有着广泛的应用，例如网络分析、社交网络分析和路由算法。

### 稀疏矩阵在图论中的应用

在图论中，稀疏矩阵经常被用来表示图。图中的顶点对应于稀疏矩阵的行和列，而边对应于稀疏矩阵中的非零元素。稀疏矩阵可以有效地表示图的结构，因为大多数图都是稀疏的，即只有少数边连接着顶点。

### 图论中稀疏矩阵存储格式的选择

在图论中，选择合适的稀疏矩阵存储格式对于优化算法性能至关重要。CSR、CSC和LIL存储格式各有优缺点，具体选择取决于图的结构和算法需求。

| 存储格式 | 优点 | 缺点 |
|---|---|---|
| CSR | 访问行快速 | 访问列慢 |
| CSC | 访问列快速 | 访问行慢 |
| LIL | 构建和修改快速 | 访问行和列都慢 |

### 案例：使用CSR存储格式表示图

考虑一个有5个顶点和6条边的无向图。图的邻接矩阵如下：

[0 1 0 0 1]
[1 0 1 0 0]
[0 1 0 1 0]
[0 0 1 0 1]
[1 0 0 1 0]

使用CSR存储格式表示该图的邻接矩阵：

indptr = [0 2 4 6 8 10]
indices = [1 2 3 2 4 5]
data = [1 1 1 1 1 1]

其中：

* `indptr`表示每行非零元素的起始位置。
* `indices`表示每行非零元素的列索引。
* `data`表示每行非零元素的值。

### 稀疏矩阵在图论中的优化

稀疏矩阵存储格式的优化对于图论算法的性能至关重要。一些常见的优化技术包括：

* **压缩存储：**使用更紧凑的数据结构来存储稀疏矩阵，例如Elias-Fano编码。
* **结构重排序：**对稀疏矩阵进行重排序，以减少非零元素的访问时间。
* **并行算法：**利用多核处理器或GPU来并行处理稀疏矩阵操作。

# 5.1 稀疏矩阵存储格式的优化算法

为了提高稀疏矩阵存储格式的效率，可以采用各种优化算法。这些算法主要集中在减少存储空间和提高计算效率两个方面。

### 压缩算法

压缩算法通过减少存储非零元素的数量来优化存储空间。常用的压缩算法包括：

- **零跳跃编码（ZJC）：**将连续的零元素编码为一个跳跃长度。
- **差分编码：**将非零元素与前一个非零元素的差值进行编码。
- **算术编码：**将非零元素的概率分布进行编码，从而实现更紧凑的表示。

### 排序算法

排序算法通过对非零元素进行排序来提高计算效率。常用的排序算法包括：

- **按行排序（CSR）：**将非零元素按行号排序。
- **按列排序（CSC）：**将非零元素按列号排序。
- **按值排序（LIL）：**将非零元素按值大小排序。

### 混合算法

混合算法结合了压缩算法和排序算法的优点。例如，**CSR-ZJC**算法将CSR存储格式与ZJC压缩算法相结合，既能节省存储空间，又能提高计算效率。

## 5.2 稀疏矩阵存储格式的优化技术

除了优化算法之外，还可以采用一些优化技术来提高稀疏矩阵存储格式的效率。这些技术包括：

### 缓存优化

通过将稀疏矩阵存储在缓存中，可以减少内存访问次数，从而提高计算效率。

### 并行化

通过将稀疏矩阵存储格式的计算任务并行化，可以充分利用多核处理器，进一步提高计算效率。

### 稀疏矩阵分解

通过对稀疏矩阵进行分解，可以将其表示为多个较小的稀疏矩阵，从而简化计算过程，提高效率。