Python分治法高效寻找二维数组局部峰值

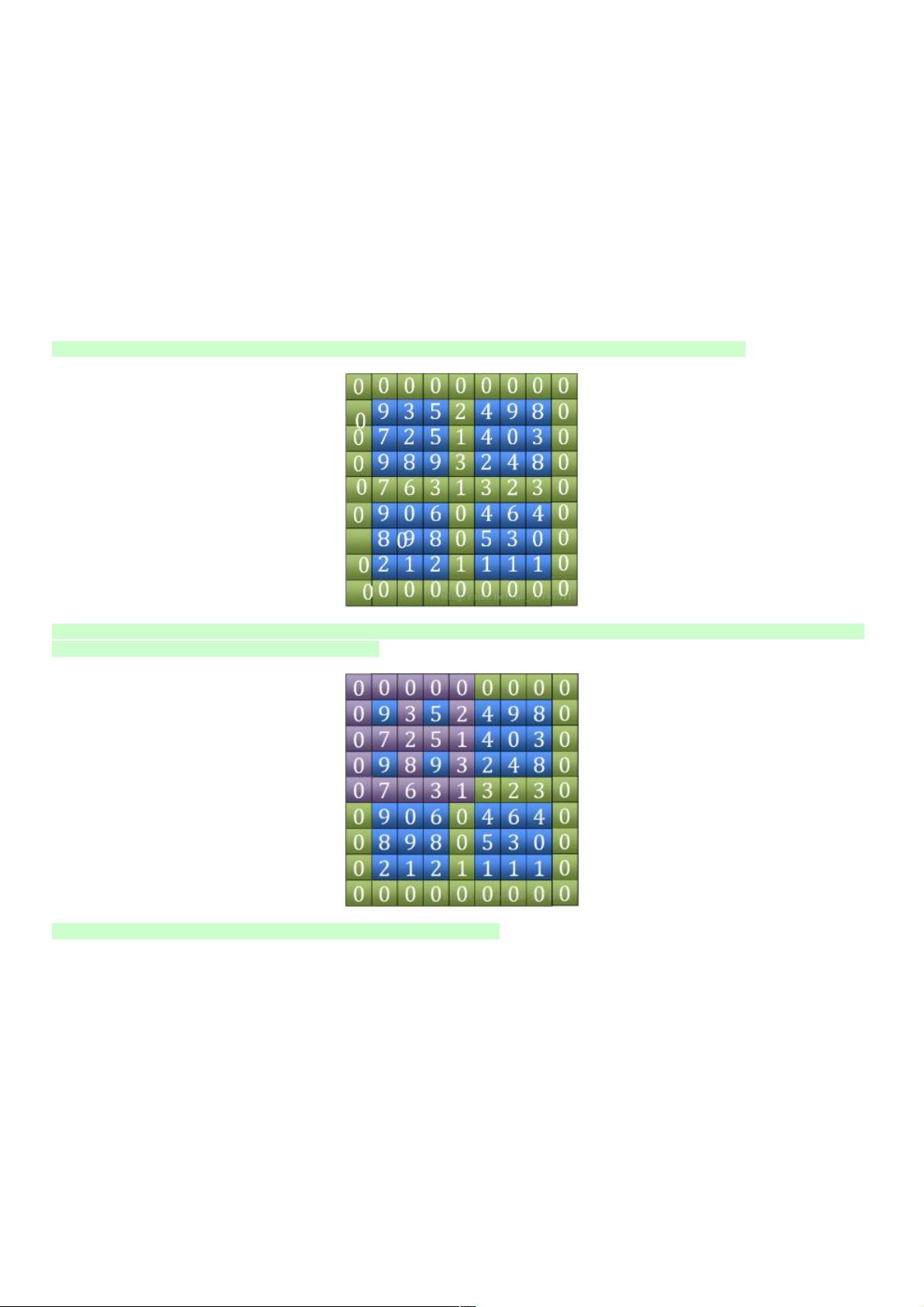
在Python中，求二维数组的局部峰值问题可以使用分治法进行高效解决。这个算法的主要目标是在一个给定的n*m大小的二维数组中找到局部峰值，即满足条件A[j][i]大于其四个相邻元素的值。题目要求的峰值定义为：A[j][i] > A[j+1][i], A[j][i] > A[j-1][i], A[j][i] > A[j][i+1], A[j][i] > A[j][i-1]。 传统的解决方法是线性扫描遍历整个数组，时间复杂度为O(n^2)，但效率较低。为了提高效率，可以采取以下两种优化策略： 1. **一维优化**：首先对每一行（或列）求最大值，然后使用二分查找法找到每行最大值所在列的峰值。这种方法的时间复杂度降低到了O(logn)。 2. **分治法**：本文介绍了一种更高效的O(n)复杂度算法。算法步骤如下： - **田字区域搜索**：首先找出矩阵中包含外部边界和内部“田”字结构的区域，找出这些区域中的最大值，如图中的7所示。 - **局部峰值判断**：如果找到的最大值满足峰值条件，则返回坐标；若不满足，记录其相邻四个点中的最大值坐标，并根据象限缩小搜索范围。 - **逐步缩小范围**：当搜索范围缩小到3x3时，由于已知存在一个大于周围元素的值，必然能找到局部峰值，即使之前已经找到也可能在更小的范围内。 下面是Python代码实现，其中`max_sit`函数用于找到列表中最大值的位置，而`dp`函数则是分治算法的核心部分，通过递归处理子矩阵来寻找峰值。 ```python import numpy as np def max_sit(*n): # 返回最大元素的位置 temp = 0 sit = 0 for i in range(len(n)): if (n[i] > temp): temp = n[i] sit = i return sit def dp(s1, s2, e1, e2): m1 = int((e1 - s1) / 2) + s1 # 行索引 m2 = int((e2 - s1) / 2) + s2 # 列索引 nub = e1 - s1 temp = 0 sit_row = 0 sit_col = 0 for i in range(nub): t = max_sit(list(array[s1+m1-i:e1-m1+i+1, s2+m2:i+1])) if t > temp: temp = t sit_row = s1+m1-i sit_col = m2 return sit_row, sit_col, temp # 使用示例： array = np.array([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10], [11, 12, 13, 14, 15], [16, 17, 18, 19, 20]]) peak_row, peak_col, peak_value = dp(0, 0, len(array)-1, len(array[0])-1) print(f"局部峰值坐标: ({peak_row}, {peak_col}), 值: {peak_value}") ``` 这个分治法求二维数组局部峰值的算法利用了数组结构的特性，避免了不必要的遍历，从而显著提高了效率。理解并应用这个算法可以帮助你更好地处理这类二维数据的峰值查找问题。