二叉树遍历与Catalan数：算法解析与应用

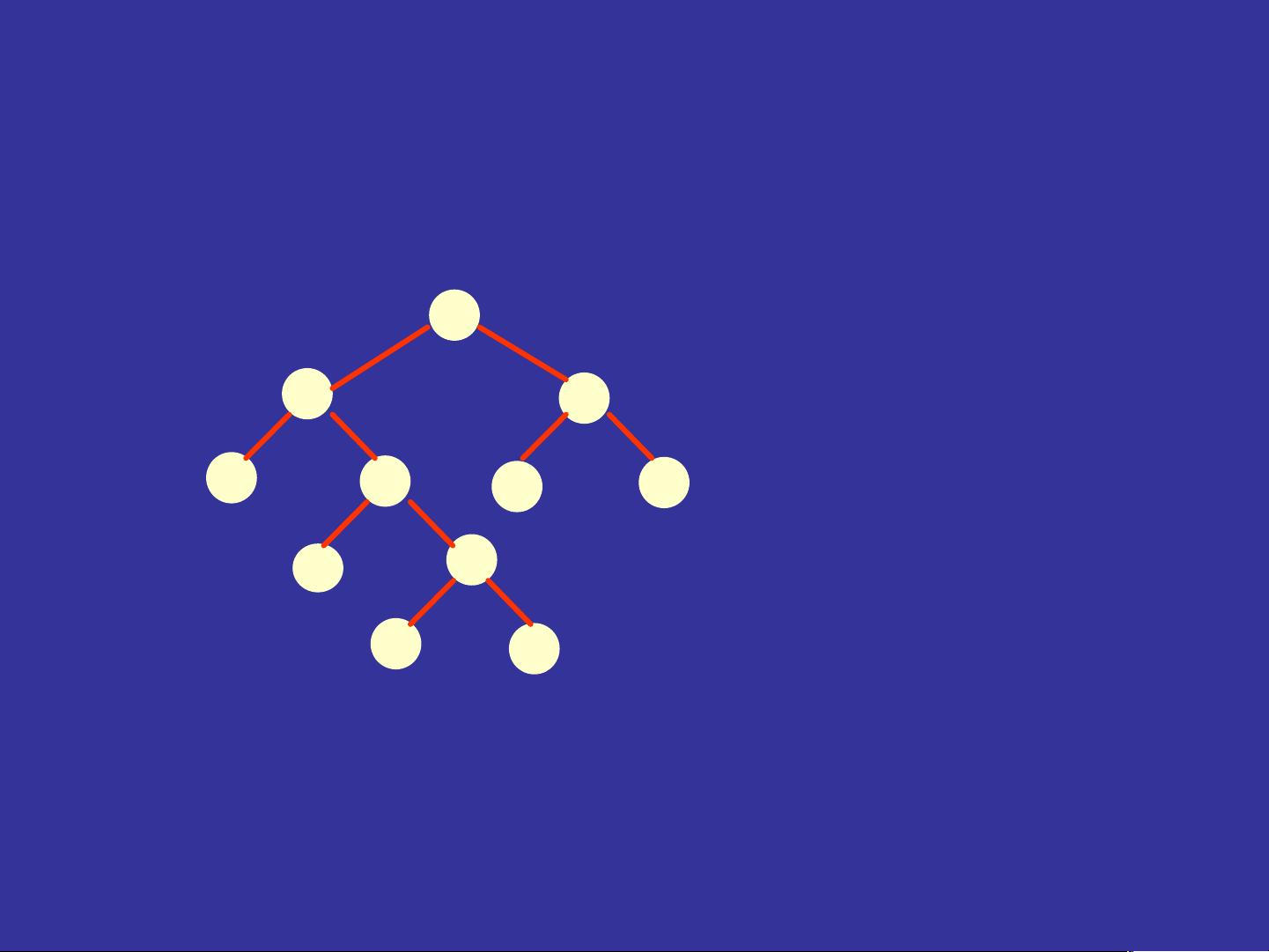
"这篇资源主要讨论了二叉树的遍历方法和Catalan数的应用。二叉树的遍历包括先序、中序、后序三种方式，每种方式都涉及对根节点、左子树和右子树的访问。而Catalan数是一种在信息学问题中常见的计数工具，可以通过递推公式来计算，常用于解决如排列限制、栈操作序列等问题。" 在二叉树的遍历中，我们通常关注三种主要的方法： 1. **先序遍历** (DLR): 访问根节点 -> 遍历左子树 -> 遍历右子树。这是最常见的遍历方式，它首先访问当前节点，然后递归地处理左右子树。 2. **中序遍历** (LDR): 遍历左子树 -> 访问根节点 -> 遍历右子树。在二叉搜索树中，中序遍历可以得到节点从小到大的排序。 3. **后序遍历** (LRD): 遍历左子树 -> 遍历右子树 -> 访问根节点。后序遍历常用于计算表达式树等场景，因为它可以按照运算符优先级进行计算。 Catalan数是一个在计算机科学和数学中非常重要的序列，其递推公式为 `h(n) = Σ(h(i) * h(n-i))` 对于 `i=0` 到 `i=n-1`，且 `h(0) = h(1) = 1`。Catalan数具有多种应用，例如： - **计数问题**: 例如，给定n个A和n个B，满足任何时候B的数量不超过A的数量的排列数量，可以使用Catalan数解决。 - **栈操作序列**: 当涉及到栈的进栈和出栈操作，且要求在任何时候栈中元素的个数非负，Catalan数可以用来计算满足条件的不同操作序列的数量。 - **二叉树的形态计数**: 求解N个节点的不同形态的二叉树数目也与Catalan数有关。每个形态的二叉树可以看作是一个满足特定条件的二维矩形区域划分问题，从而可以转化为计算Catalan数。 在解决实际问题时，将问题转化为Catalan数问题模型是关键，这通常需要分析问题的递归结构并确认是否符合Catalan数的计数特性。通过将问题与Catalan数的递推关系联系起来，我们可以有效地解决这些问题。在编程竞赛和算法设计中，理解并掌握这些概念和技巧是非常重要的，它们可以帮助我们高效地处理复杂的数据结构和计数问题。