转化递归问题：二叉树先序排列与Catalan数应用

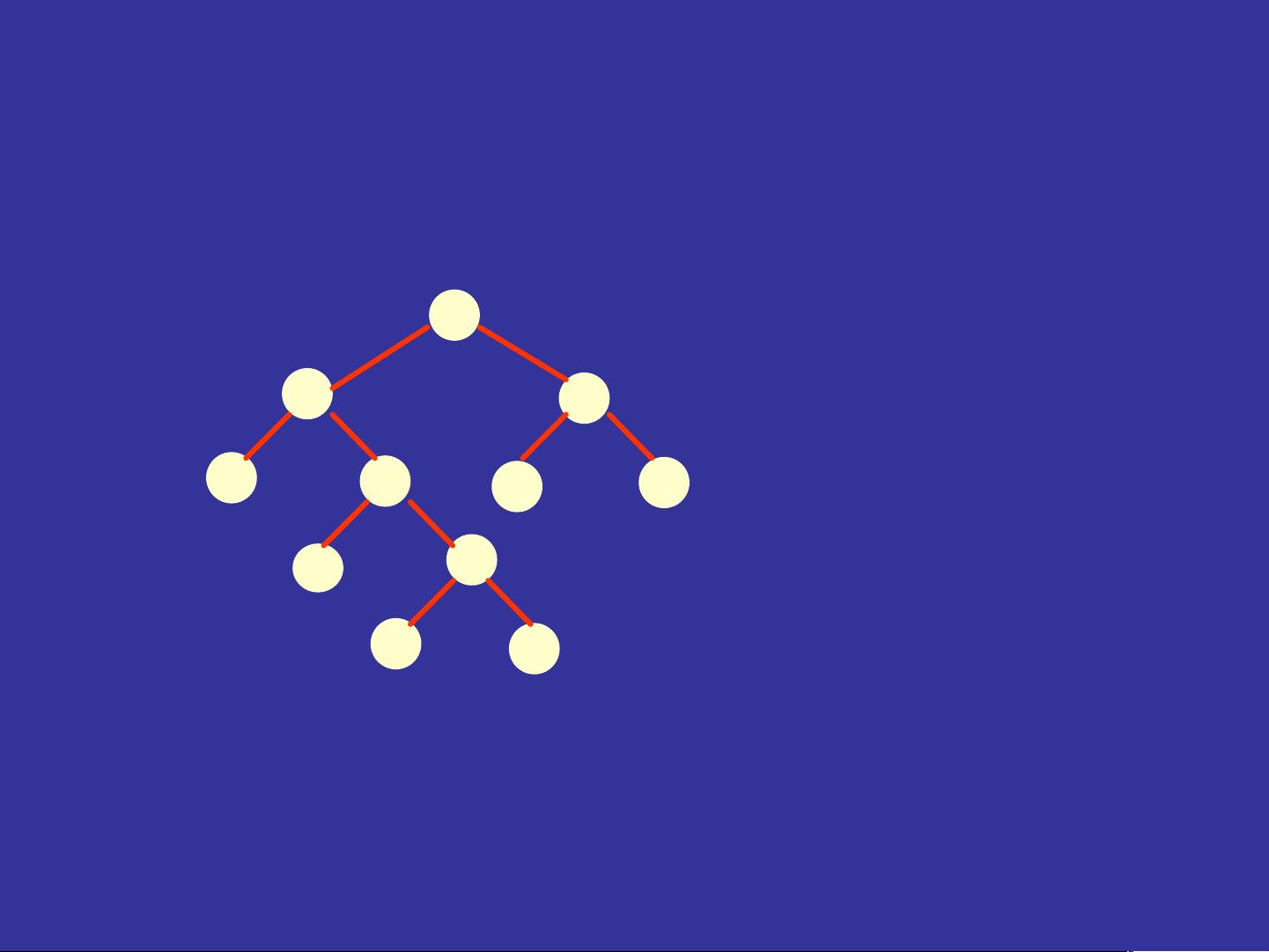
在IT领域的算法专项练习中，涉及到递推与递归的问题探讨，特别是针对二叉树的遍历问题。题目要求求解给定一棵二叉树的先序排列，已知其中序和后序遍历。这个任务实际上涉及到了树形结构的处理，特别是通过递归和回溯的方法来解决。 首先，我们需要理解什么是先序遍历，它是访问二叉树节点的一种标准顺序，即先访问根节点，然后递归地访问左子树，最后访问右子树。要解决这个问题，我们通常会利用线索二叉树或者通过递归构建先序序列。线索二叉树是通过在节点上添加额外的信息，使得遍历过程更加直观和高效。 在讨论算法过程中，引入了Catalan数的概念。Catalan数是一种重要的组合数学序列，它在解决许多计数问题中扮演关键角色，如平衡括号、路径遍历、图的着色等。Catalan数的递归定义是通过h(n)与前两个数的乘积之和，其递推公式表达式为h(n) = h(0) * h(n-1) + h(1) * h(n-2) + ... + h(n-1) * h(0)，对于n >= 2。这个问题的分析关键在于找到问题与Catalan数递归式的对应关系。 例如，给出的例题是一个经典的Catalan数问题模型，描述的是n个A和n个B如何排列，以确保B的数量始终不超过A。通过观察，我们可以看出，这个问题的解决方案可以用Catalan数的定义来表示，即满足“0”的累计数不大于“1”的累计数的二进制数，这与二叉树的先序遍历中的节点入栈和出栈操作相似，都是关于操作序列中1和0数量的关系。 对于实际的二叉树先序遍历问题，可以通过递归实现。在递归函数中，我们可以定义一个基本情况，如空树的先序为空，非空树的先序则为根节点加上左子树的先序和右子树的先序。在递归调用中，我们按照先序遍历的原则依次处理左右子树，直到遍历完整棵树。 总结来说，解决二叉树先序排列的问题，需要理解递归和递推的基本概念，尤其是如何通过Catalan数的思想转化问题，将其转化为操作序列的问题，进而利用递归的技巧来生成先序遍历序列。通过这些方法，可以有效地求解给定二叉树的先序排列。