栈问题与Catalan数：递推与递归算法应用

栈问题分析是算法专项练习中的一个重要主题，主要涉及递归和递推方法。栈是一种数据结构，其基本操作包括入栈（进栈）和出栈。在这个问题中，我们面对的是一个特定的模式，即对于n个数，需要进行n次进栈和n次出栈操作，这可以通过构造一个2n位的二进制序列来表示，其中1代表进栈，0代表出栈。关键在于保持栈内元素数量始终大于等于0，意味着任何时候“1”的累计数都大于或等于“0”的累计数。 原问题转化为寻找所有满足这种条件的二进制序列，即“0”的累计数不超过“1”的累计数。这个任务与Catalan数相关，Catalan数是一个重要的数列，它满足递归公式： \[ h(n) = \frac{1}{n+1} \binom{2n}{n} = \frac{(2n)!}{(n+1)! \cdot n! \cdot n!} \] Catalan数问题通常用于解决一类特定类型的组合问题，如平衡括号的数量、非交叉的路径数量等。在栈问题中，我们需要将问题转化为Catalan数问题模型，通过观察序列中1和0的交替出现，找到满足条件的序列数量。 例如，对于序列123，我们可以将其转换为231，对应的操作序列是： ``` 123 -> 23 3 -> 31 1 -> 1 31 -> 1 ``` 每一步操作都是根据栈的状态进行的，确保栈中始终有大于或等于0的元素。最终的10序列满足了“0”的累计数不超过“1”的累计数。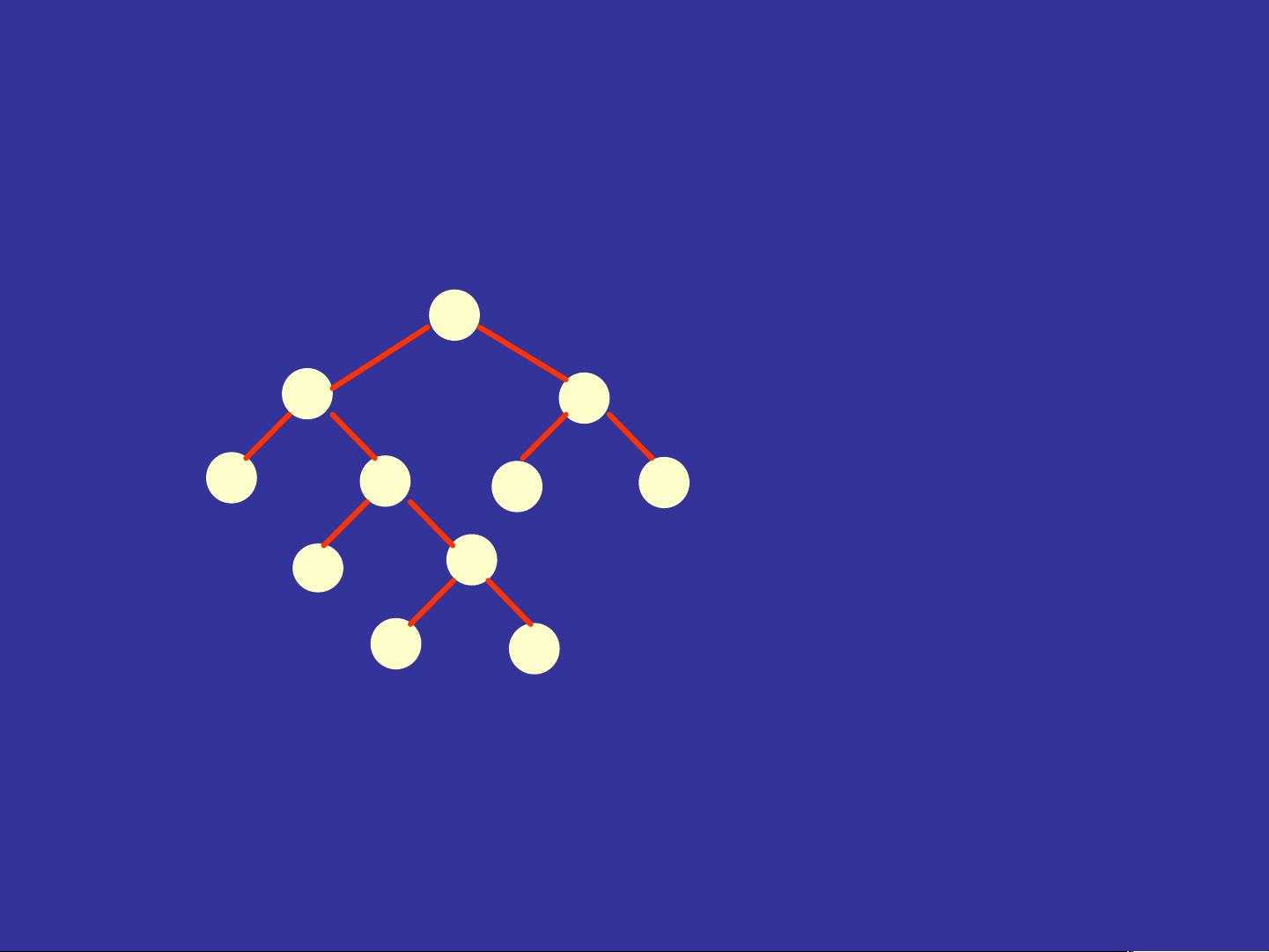 对于更复杂的问题，比如求解N个节点构成的不同形态的二叉树数目，二叉树的定义是一个关键概念。二叉树是每个节点最多有两个子节点的树结构，且左右子树不能颠倒，这使得计算二叉树的数量成为一个典型的递归问题。通过递归的方法，我们可以利用Catalan数的性质来求解这类问题，但具体步骤会涉及到递归函数定义、边界条件、以及递归调用等算法技巧。 总结来说，栈问题分析涉及将实际问题与Catalan数的递归性质相结合，通过递归和递推方法，找出满足特定栈操作条件的序列，解决了一系列与二叉树形态相关的问题。理解和掌握这个问题的关键在于理解Catalan数模型的构造和应用，以及如何将实际问题映射到这个模型中。