Catalan数在算法中的应用分析
需积分: 5 138 浏览量
更新于2024-07-14
收藏 406KB PPT 举报
"思路分析-算法专项练习--递推与递归"
本文主要探讨了算法中的递推与递归思想,并通过具体的例子介绍了如何应用这些概念。首先,我们关注的是如何判断括号是否多余,这涉及到运算符的优先级和括号的保留规则。在处理表达式时,如果左邻括号的运算符为除法'/',那么不论括号内的运算符是什么,括号都必须保留,因为去除括号会改变表达式的含义,可能导致除数发生变化。
接下来,我们讨论了Catalan数及其递推公式。Catalan数是一类在计算机科学和组合数学中有广泛应用的数,它满足特定的递推关系。对于n>=2,Catalan数h(n)可以通过以下递推关系计算:
\[ h(n) = \sum_{k=0}^{n-1} h(k) \cdot h(n-1-k) \]
简化后的形式是:
\[ h(n) = \frac{1}{n+1} \binom{2n}{n} \]
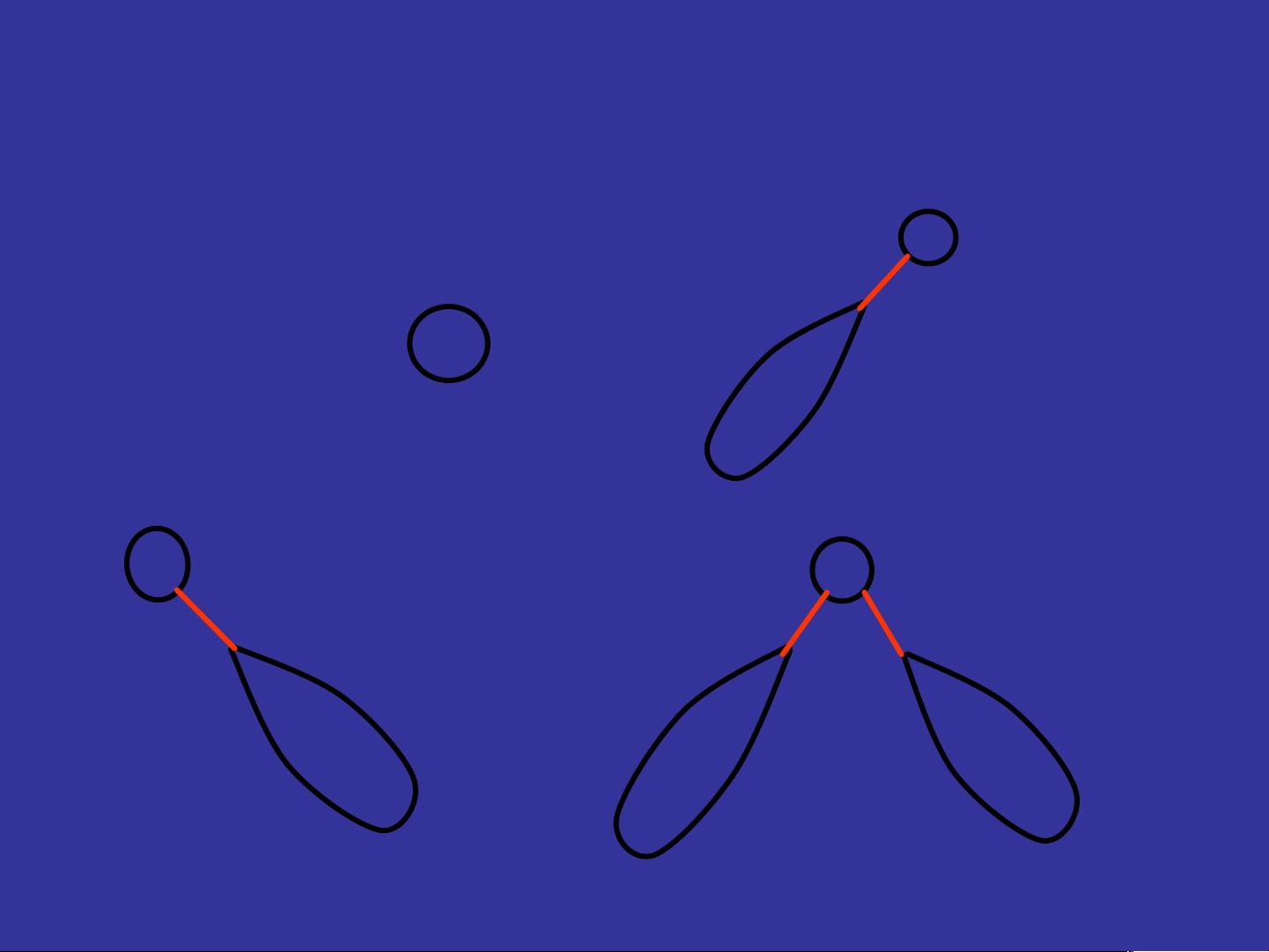
Catalan数常用于解决各种组合问题,例如排列和组合计数问题。在信息学问题分析中,将问题转化为Catalan数问题模型是非常重要的。例如,当有n个A和n个B需要排列,且任何时候B的数量不能超过A的数量时,这个问题可以转化为Catalan数问题。
此外,递推和递归的思想也常用于栈问题。栈的进栈和出栈操作可以表示为1和0,一个有效的操作序列要求在任何时候"0"的累积数量不超过"1"的累积数量。这与寻找满足特定条件的二进制序列问题相似,同样可以用Catalan数来解决。
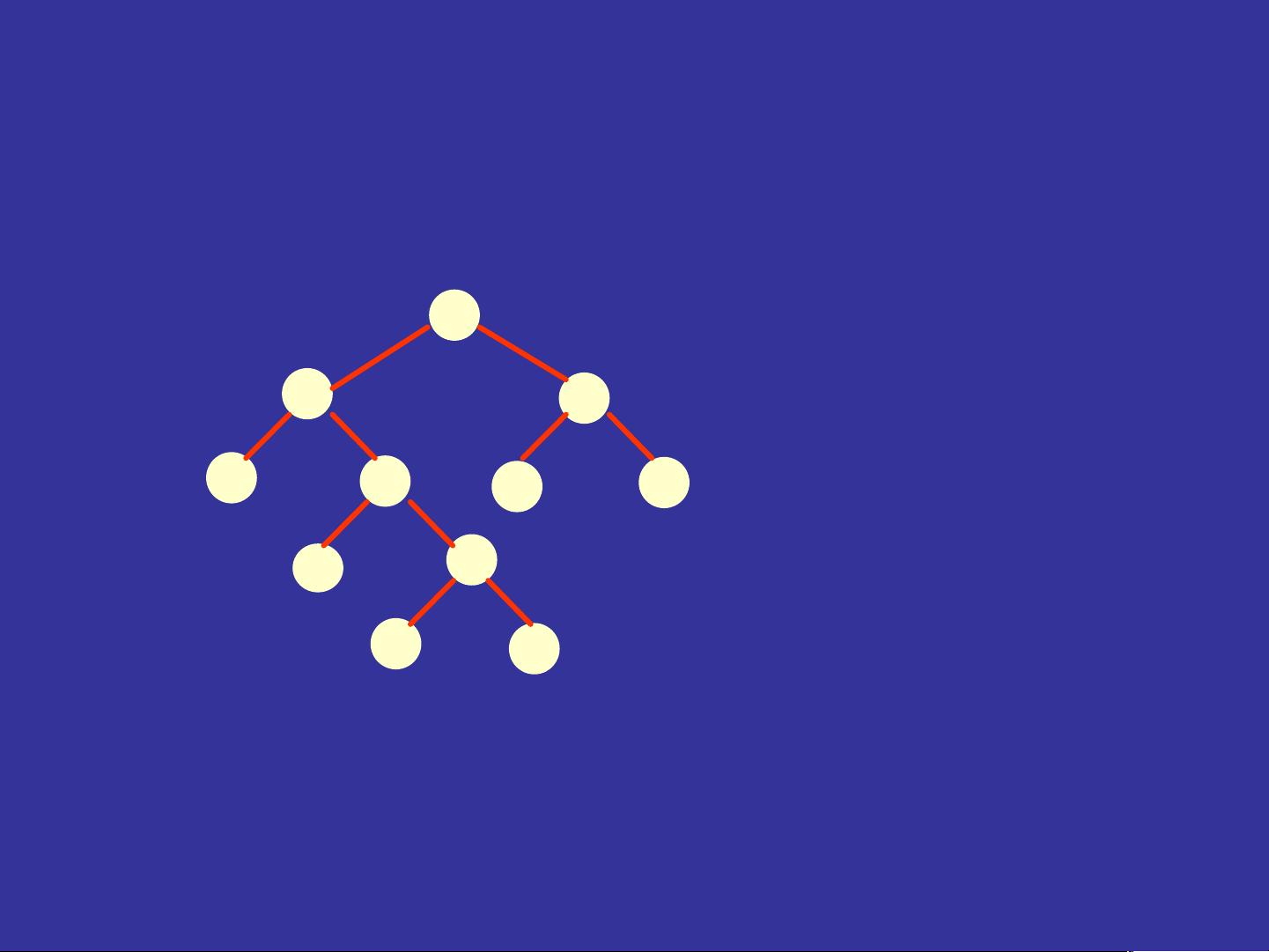
最后,递归在构建二叉树形态的问题中也发挥着重要作用。二叉树是由根节点和两棵非交叉的左子树和右子树构成的结构,递归地定义了二叉树的每个节点。通过递归函数,我们可以生成所有可能的二叉树形态,每棵树的形态对应于一个特定的构造过程,从而计算出N个节点的不同形态的二叉树总数。
递推和递归是算法设计中的核心概念,它们广泛应用于解决各种复杂问题,包括括号的有效性检查、组合计数、栈操作序列以及二叉树的构造。理解和熟练掌握这些算法技巧对于提升编程能力至关重要。
2021-10-06 上传
点击了解资源详情
点击了解资源详情
点击了解资源详情
点击了解资源详情
点击了解资源详情
Happy破鞋
- 粉丝: 14
- 资源: 2万+
最新资源
- 个人数字证书与CA认证.pdf
- Electronics Workbench(ewb)简明中文教程
- 单片机设计题目要求 温度计
- C语言嵌入式系统编程修炼之道.pdf
- Java swing学习课件
- JavaEye论坛热点_-_2008年11月
- C++标准程式库.pdf
- VC++2005入门经典(英文版).pdf
- 2009年计算机等级考试四级数据库工程师考试 课后答案
- 手工创建数据库,在命令提示符下的创建操作步骤.
- J2ME企业级开发-j2me
- 雅思听力807词汇表
- [教程] 权威揭密 笔记本硬件结构终极教程&_8226_(上、中、下)
- 编程相关日语词汇 基本的
- ITIL_V3的五大生命周期管理.pdf
- 2009年计算机等级考试四级数据库工程师考试重难点