LINDO与LINGO：QP问题求解与实例讲解

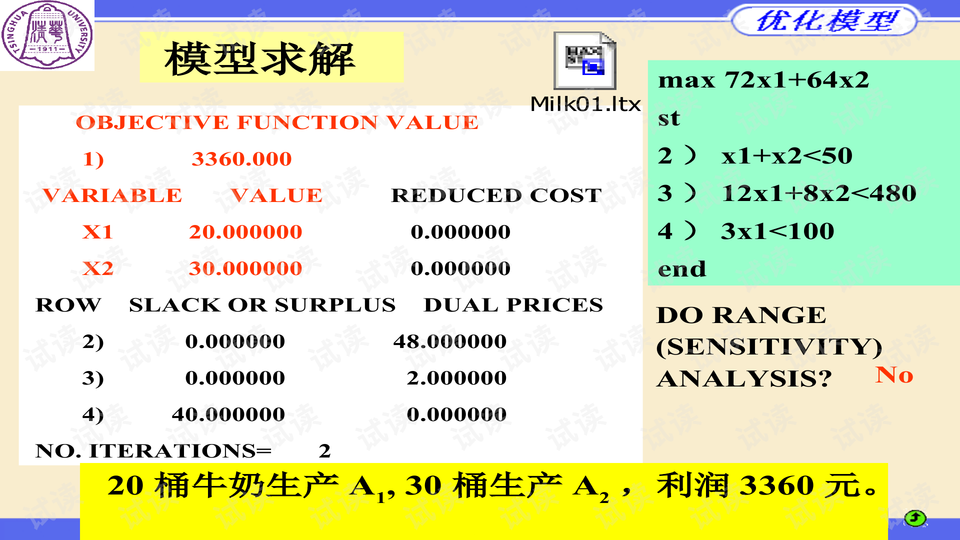
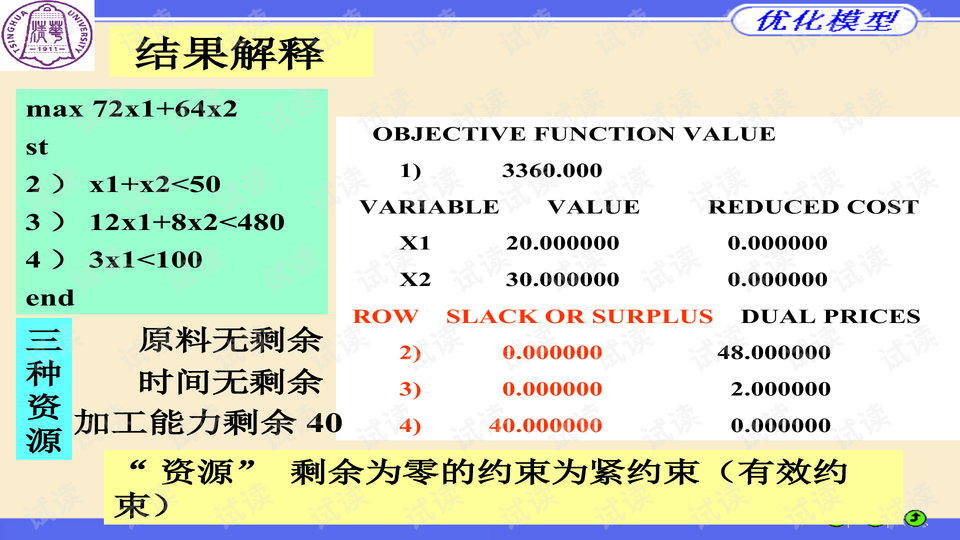
二次规划问题(QP)是数学优化领域中的一个重要分支，特别是在线性规划和非线性规划之间。在LINDO和LINGO这类优化软件中，它具有广泛的应用。LINDO，由美国芝加哥大学Linus Schrage教授开发，是一个既能处理线性交互式又能解决离散优化问题的工具，其主要版本包括LINDO、LINGO以及LINDO API。LINDO V6.1专攻线性优化，而LINGO V8.0则更进一步，能够处理线性、非线性和二次规划问题，包括连续优化和整数规划。 在LINDO中，由于其输入方式不允许直接表达非线性，解决QP问题时需要进行一些转换。这涉及到为每个实际约束添加对偶变量（拉格朗日乘子），并在约束前引入一阶最优条件，将其转化为互补形式，使得问题可以被LINDO处理。用户需要明确指出实际约束的开始行号，通过使用"QCP"命令来启动求解过程。 尽管敏感性分析在QP和整数规划（IP）中可能不如其他类型的规划显著，但这些软件依然提供了广泛的求解能力。LINDO和LINGO都支持线性规划（LP）、非线性规划（NLP）、二次规划（QP）、连续优化以及部分整数规划，如纯整数规划（PIP）和混合整数规划（MIP）。对于那些包含全局优化选项的模型，如LP、QP、NLP和ILP，用户可以根据需求选择相应的求解策略。 在使用LINDO/LINGO时，软件的求解过程通常包括预处理程序，如常数确定和问题类型的识别。线性优化采用单纯形算法，而非线性优化则可能依赖于数值方法。对于整数规划，LINDO/LINGO会运用分枝定界等算法来寻找最优解。 在实际建模和求解过程中，LINDO和LINGO提供了丰富的例子和教程，帮助用户通过软件操作将实际问题转化为数学模型，并执行求解。清华大学数学科学系的谢金星教授的讲座系列，为学习者提供了优化模型介绍、软件功能概述以及如何使用这两种工具进行建模和求解的深入指导。 二次规划问题在LINDO和LINGO中得到了高效且灵活的解决，软件提供了多种优化模型的支持，包括线性、非线性和整数规划，以及对应的求解策略和预处理步骤，为实际问题的优化决策提供了强大工具。