无人机编队无源定位技术：纯方位定位模型与策略

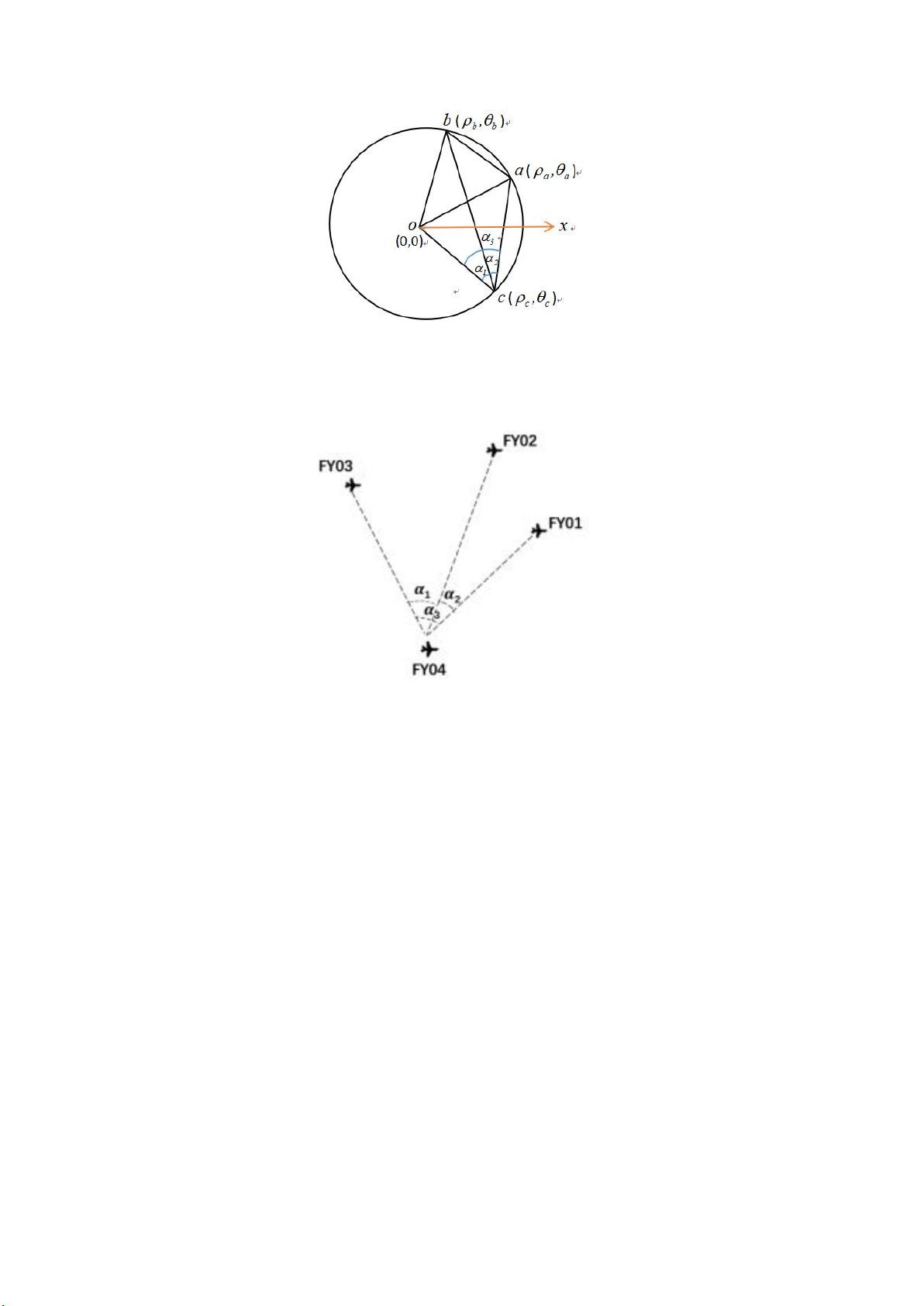
"基于纯方位无源定位的无人机定位问题，2022数学建模A题题解" 本文主要探讨的是无人机群在执行编队飞行任务时，如何利用纯方位无源定位技术来精确地定位每个无人机的位置，同时保持编队的几何形状，特别是圆形和锥形编队。纯方位无源定位是一种无需直接通信，而是通过接收信号源的相对方位信息来确定目标位置的技术。这种方法在保持电磁静默和节省通信资源方面具有显著优势。 首先，文章深入剖析了纯方位无源定位的原理，指出它依赖于三角函数中的余弦定理。通过构建无人机间的相对位置三角形，可以建立无人机的定位模型。无人机FY00被设定为极点，建立极坐标系，而无人机FY01与FY00的连线作为极轴。利用发射信号无人机和接收信号无人机之间的相对位置，可以形成多个三角形，进而利用余弦定理推导出无人机的极坐标表示，即距离（ρ）和角度（θ）。 在已知两架发射信号无人机（如FY00和FY01）的情况下，每架接收信号的无人机只能与这两架之一构成一个三角形。为了准确地定位并调整所有无人机的位置，至少需要第三个参考点，即另外一架发射信号的无人机。通过计算不同无人机间的夹角，可以确定这架新增无人机的编号和位置。 接下来，将极坐标转换为直角坐标系，便于计算无人机需要调整的方向和距离。这个坐标系以FY00为原点，FY00和FY01的连线为x轴，FY01方向为正。通过无人机实际位置与理想位置的差异，可以计算出每个需要调整的无人机的偏航角和移动距离。例如，FY02需要偏航-94.0083°，移动0.6867m，而FY03则需偏航-103.0364°，移动12.9539m等。 无人机的调整方案是基于机载坐标系制定的，该坐标系以无人机自身为原点，横轴与原坐标系平行，行进方向为正向。这样，每个无人机都能根据自身的偏航角和移动距离进行精确调整，以达到编队保持的目的。 本论文通过数学建模方法，解决了无人机编队飞行中基于纯方位无源定位的定位问题，提出了一套有效的无人机位置调整策略，确保了在保持电磁静默的同时，能够维持编队的几何形状，对于无人机群的自主导航和协同控制具有重要的理论与实践意义。