"随机信号分析大作业1：复合信号分析和功率谱密度研究"

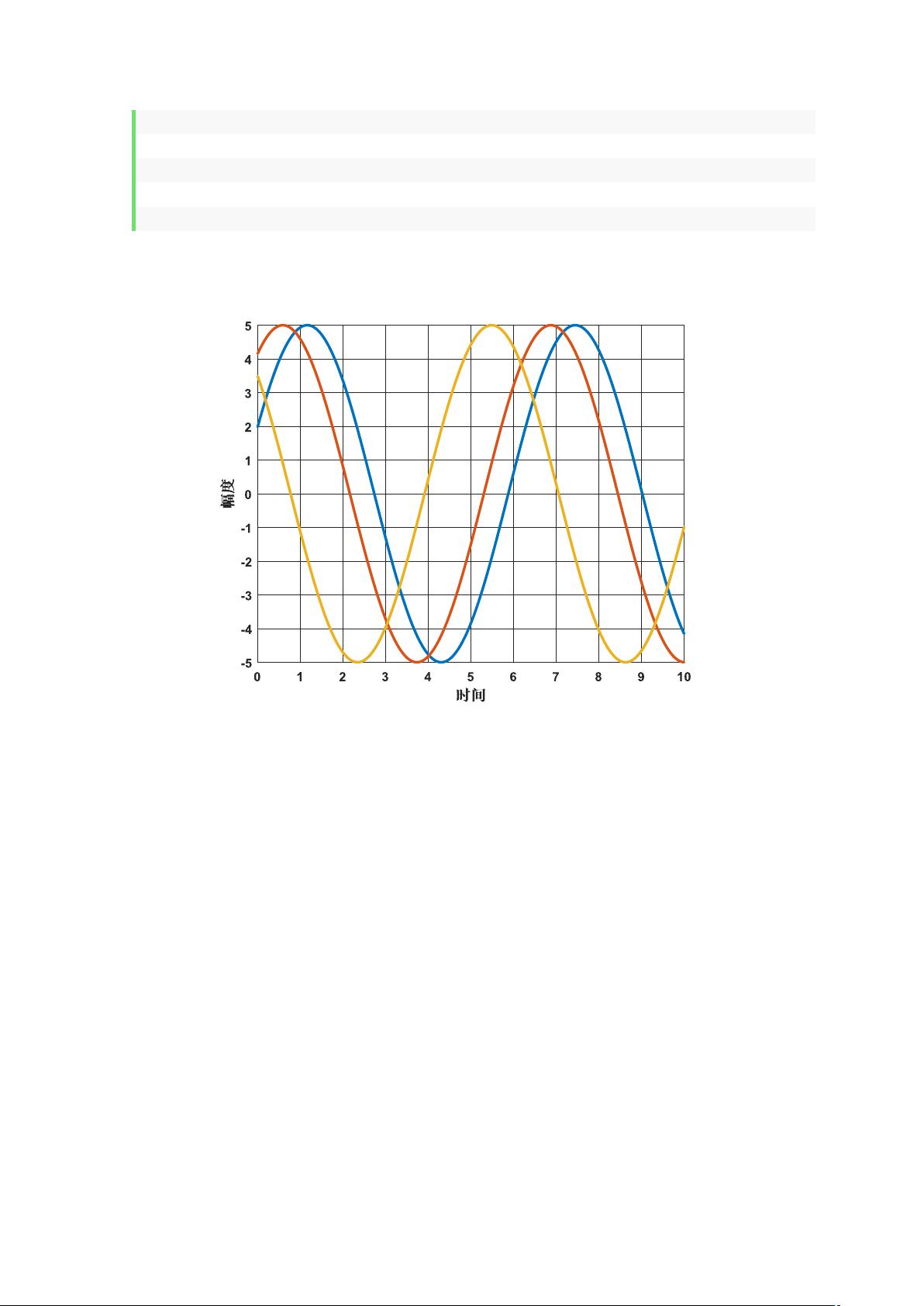
到2π之间均匀分布的三个随机数，然后利用这三个随机数分别代入初始相位信号函数5cos(t+j)，并以此生成三个样本函数。具体实现代码如下： ```MATLAB clear all; clc; t = 0:0.01:10; % 生成时间序列 j = 2*pi*rand(1,3); % 生成3个0~2π之间均匀分布的随机数 X1 = 5*cos(t + j(1)); % 第一个样本函数 X2 = 5*cos(t + j(2)); % 第二个样本函数 X3 = 5*cos(t + j(3)); % 第三个样本函数 ``` 通过以上代码，我们成功地生成了三个随机初相信号的样本函数。接下来，我们将以这些样本函数为基础，进行复合信号的分析和功率谱密度的计算。 2.2 复合信号的功率谱密度分析 在此部分，我们将对由正弦型信号加高斯白噪声组成的复合信号进行功率谱密度的计算和分析。具体实现代码如下： ```MATLAB N = length(t); % 获取样本函数的长度 Fs = 1/(t(2)-t(1)); % 计算采样频率 n = 2^nextpow2(N); % 计算FFT的点数，取大于N的最小的2的正整数次幂 Y1 = fft(X1, n)/N; % 对第一个样本函数进行FFT Y2 = fft(X2, n)/N; % 对第二个样本函数进行FFT Y3 = fft(X3, n)/N; % 对第三个样本函数进行FFT f = Fs/2*linspace(0,1,n/2+1); % 构建频率坐标 P1 = 2*abs(Y1(1:n/2+1)); % 计算单侧频谱 P2 = 2*abs(Y2(1:n/2+1)); % 计算单侧频谱 P3 = 2*abs(Y3(1:n/2+1)); % 计算单侧频谱 ``` 通过以上代码，我们利用FFT算法对三个样本函数进行了频谱分析，得到了它们的功率谱密度P1、P2、P3。接下来，我们将分析复合信号的功率谱密度和幅度分布特性。 2.3 RC积分电路后的功率谱密度分析 在此部分，我们将分析复合信号通过RC积分电路后的功率谱密度和相应的幅度分布特性。具体实现代码如下： ```MATLAB RC = tf([1],[1 1]); % RC积分电路传递函数 OUT1 = lsim(RC, X1, t); % 对第一个样本函数进行RC积分电路处理 OUT2 = lsim(RC, X2, t); % 对第二个样本函数进行RC积分电路处理 OUT3 = lsim(RC, X3, t); % 对第三个样本函数进行RC积分电路处理 ``` 通过以上代码，我们成功地将三个样本函数通过RC积分电路处理，并得到了经RC积分电路后的输出信号OUT1、OUT2、OUT3。接下来，我们将对这些输出信号进行功率谱密度和幅度分布特性的分析。 2.4 理想低通系统后的功率谱密度分析 最后，我们将分析复合信号通过理想低通系统后的功率谱密度和相应的幅度分布特性。具体实现代码如下： ```MATLAB LPF = tf([1],[1 1]); % 理想低通系统传递函数 Y1 = lsim(LPF, X1, t); % 对第一个样本函数通过理想低通系统处理 Y2 = lsim(LPF, X2, t); % 对第二个样本函数通过理想低通系统处理 Y3 = lsim(LPF, X3, t); % 对第三个样本函数通过理想低通系统处理 ``` 通过以上代码，我们成功地将三个样本函数通过理想低通系统处理，并得到了经理想低通系统后的输出信号Y1、Y2、Y3。接下来，我们将对这些输出信号进行功率谱密度和幅度分布特性的分析。 通过上述实验，我们得到了随机初相信号的三个样本函数，并分别进行了复合信号、RC积分电路后的信号、理想低通系统后的信号的功率谱密度和幅度分布特性分析。通过对这些数据的分析，我们可以更加深入地了解随机信号的特性以及信号经过不同系统处理后的变化规律，为随机信号分析提供了重要的实验数据和分析手段。