人工智能与九宫格算法：八数码问题求解

"这篇资料主要介绍了使用人工智能方法解决‘八数码问题’，即经典的九宫格算法。实验目的是让学生理解状态空间搜索策略，包括盲目搜索和启发式搜索，并通过编程实现这一过程。" 在人工智能领域，九宫格算法通常指的是解决特定的逻辑谜题，例如八数码问题和十五数码问题。这两种问题都是在3x3的棋盘上进行的，其中包含了启发式搜索算法的应用。八数码问题是在棋盘上有8个数字（1到8）和1个空格，目标是通过空格的上下左右移动，将初始状态的棋盘变换为目标状态。十五数码问题则是在4x4的棋盘上，包含15个数字（1到15）和1个空格，但基本原理与八数码问题相似。 实验中使用的软件是VC6.0编程环境，但也可以使用其他编程语言来实现。核心在于构建问题的模型，定义状态和搜索策略。状态在这里是指棋盘上的数字布局，而每个状态都可以看作是问题空间中的一个节点。节点的状态包括棋盘上数字的排列、节点到目标状态的距离（dist）、节点的深度（dep，即从初始状态到该节点的操作步数）以及父节点的位置（index）。 生成器函数是解决这类问题的关键，它定义了如何根据当前状态产生新的可能状态。在这个例子中，生成器函数包括四个操作：空格上移、下移、左移和右移。每个操作都会创建一个新的节点，然后计算新节点到目标状态的距离和深度，以便后续的搜索算法使用。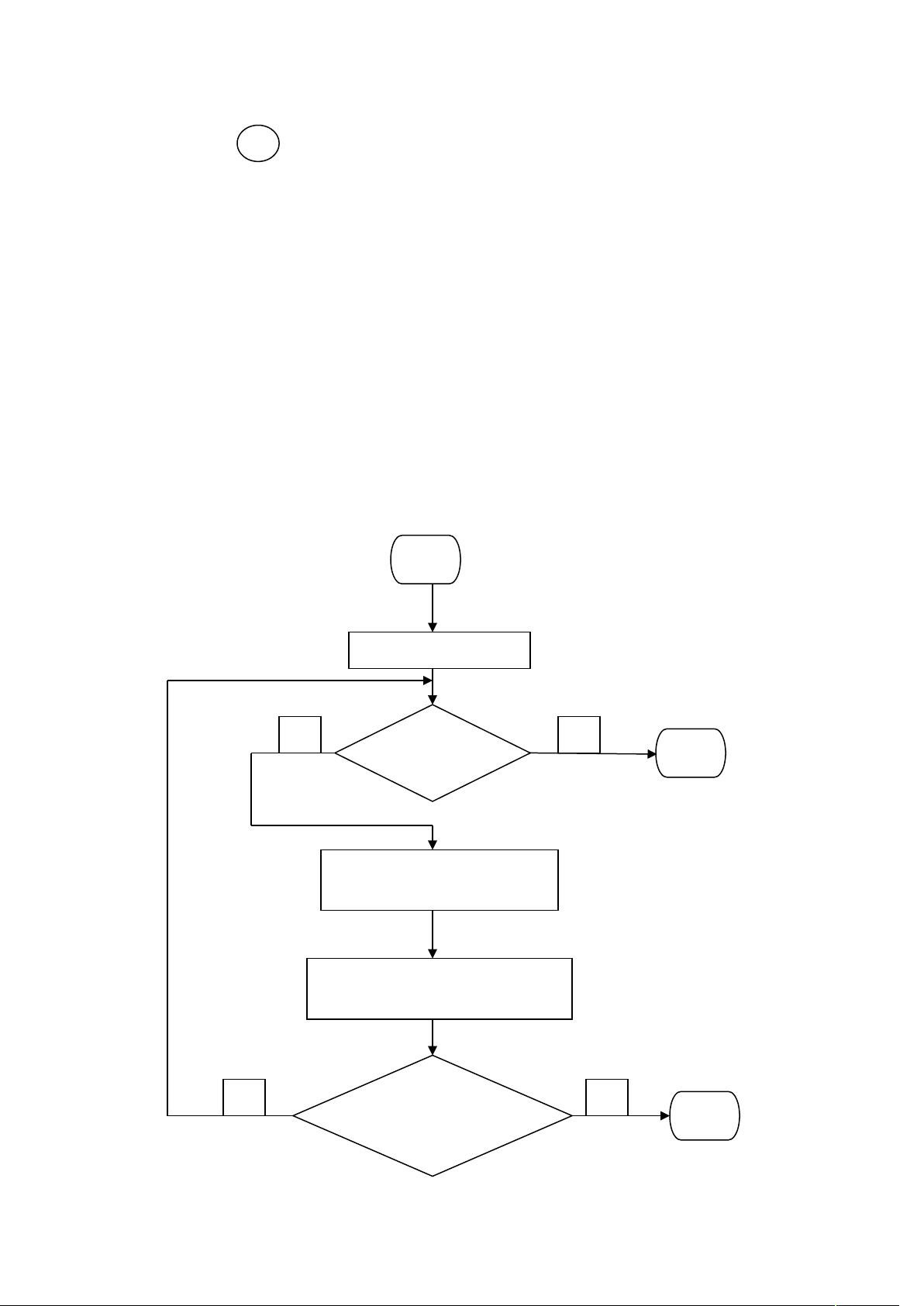 搜索策略可以分为盲目搜索（如宽度优先搜索、深度优先搜索）和启发式搜索（如A*搜索）。盲目搜索不考虑问题的具体特性，而启发式搜索会利用某种评估函数（如曼哈顿距离或汉明距离）来指导搜索，使其更高效。在这个实验中，估价函数可能是距离（dist）和深度（dep）的组合，帮助算法快速找到解决方案。 实验的主要目标是让学习者掌握人工智能中问题求解的基本流程，包括问题建模、状态表示、操作定义以及搜索算法的实现。通过解决八数码问题，学生能够实际体验到状态空间搜索策略在解决复杂问题时的有效性。