MATLAB实验：离散时间信号分析与DFT卷积

"这个文档是一个关于数字信号处理的MATLAB上机实验指导，涵盖了离散时间信号的分析，特别是通过DFT卷积进行系统时域分析的方法。实验内容包括设置不同序列并计算它们的卷积，以及自相关和互相关函数的计算。" 实验一：离散时间信号的分析主要目标是利用离散傅里叶变换(DFT)的卷积性质进行系统分析。在离散时间信号中，如果已知输入信号x[n]和系统响应h[n]，那么可以通过计算它们的DTFT（离散时间傅里叶变换），即X(ejω)和H(ejω)，将两者相乘得到Y(ejω)。然后通过IDTFT（逆离散时间傅里叶变换）得到系统输出y[n]。这种方法避免了直接在时域进行复杂的卷积运算。 实验步骤详细描述了两个具体任务。首先，创建一个序列x[k]，其中x[k]=k+1, 0<=k<=3，并将其与自身进行卷积，通过MATLAB的`conv`函数计算得到卷积结果Z，并用`stem`函数绘制波形。这展示了如何通过编程实现简单的线性卷积。 第二个任务涉及计算两个给定序列x[k]和y[k]的自相关函数以及它们之间的互相关函数。自相关函数反映信号自身的相似性，而互相关函数则衡量两个信号的相似程度。使用`conv`函数结合`fliplr`来计算自相关和互相关，然后通过`subplot`函数绘制三个不同的波形图，分别表示x[k]的自相关函数s1，x[k]与y[k]的互相关函数s2，以及y[k]的自相关函数s3。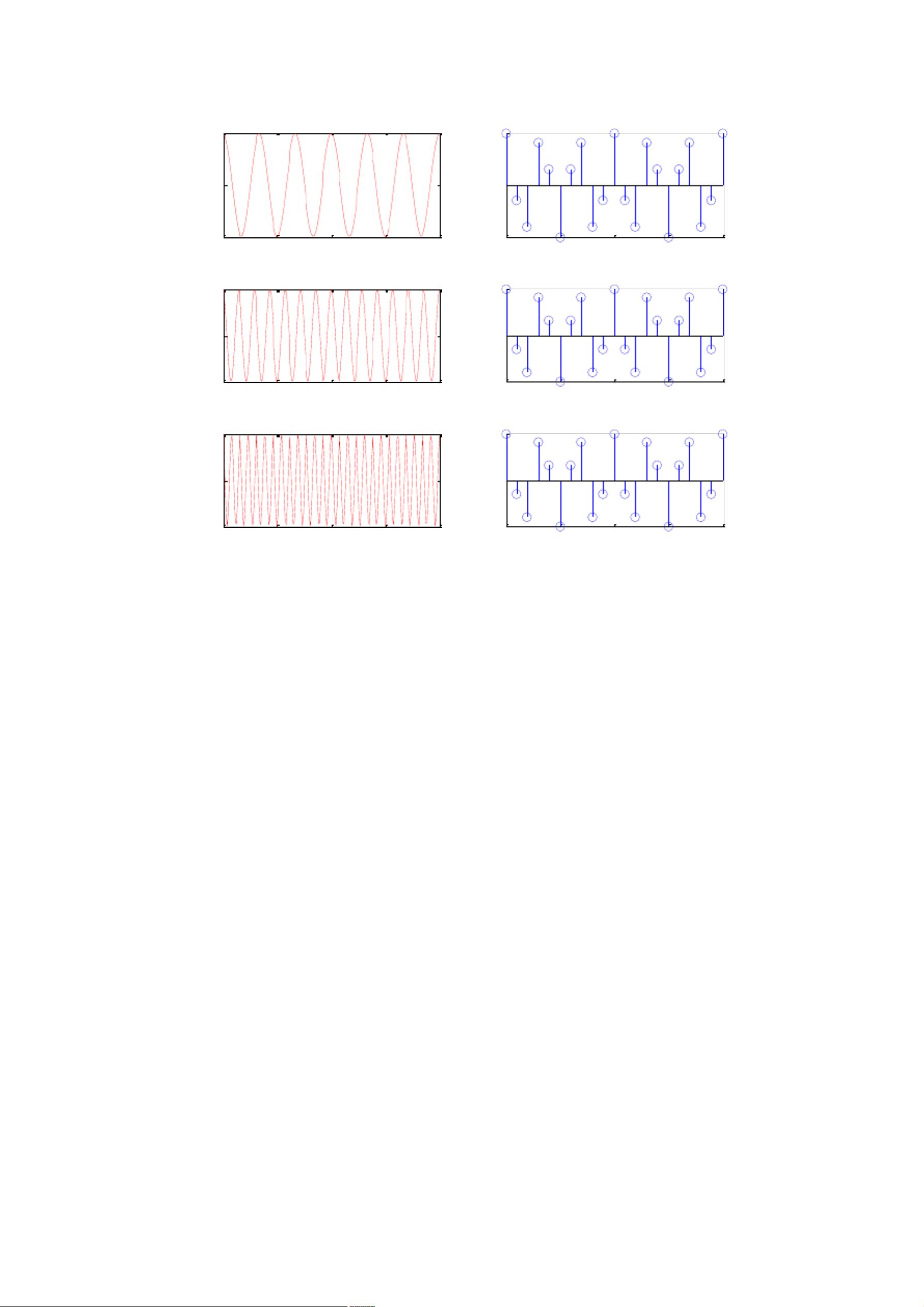 最后，实验提到了一个附加任务，即处理由不同频率成分的余弦信号g1[t], g2[t], g3[t]组成的序列，但未提供具体的实验步骤或代码。通常，这样的任务可能涉及傅里叶变换、滤波或频谱分析。 通过这些实验，学生能够深入理解离散时间信号的特性，掌握MATLAB在数字信号处理中的应用，以及如何利用DFT和卷积来分析系统响应。同时，自相关和互相关的计算有助于理解信号的时间相关性。