Java编程：最大子矩阵简便解法及代码实现

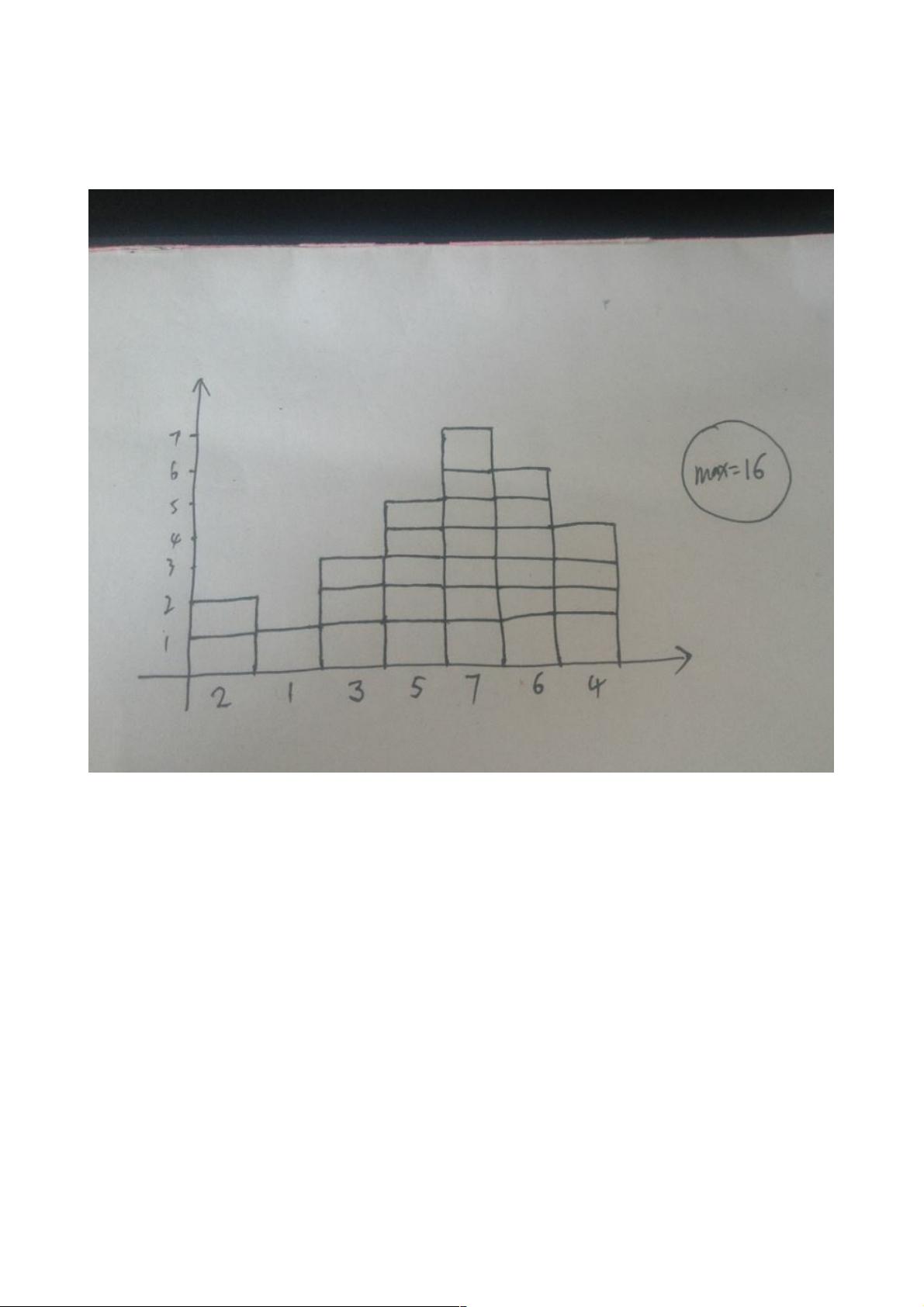
"Java编程实现最大子矩阵简便解法" 在Java编程中，解决寻找数组中最大子矩阵的问题通常涉及到算法和数据结构的应用。这个问题的一个经典解决方案是使用栈来求解，但这里介绍的是一种相对简单的算法。这种方法的核心思想是对数组进行由下至上的轮次计算，每一轮次计算出连续不间断的最大长度，从而找到最大的连续子矩阵的面积。 首先，理解算法的关键在于每次迭代都试图找到当前轮次中的最大高度，这个高度对应于连续非负数的和。例如，对于二维数组，我们可以将其视为一个柱状图，每个元素的高度等于其值。最大子矩阵的面积等同于这个柱状图中最高的连续矩形区域的面积。 算法步骤如下： 1. 初始化一个结果数组`result`，大小与输入数组`arr`相同，用于存储每一轮次的最大连续长度。 2. 遍历数组，从第二个元素开始（索引1），进行轮次计算。 3. 在每一轮次中，使用一个辅助栈来存储元素及其索引。栈顶元素表示当前连续非负数序列的起始索引。 4. 对于每个元素，如果它大于等于栈顶元素，那么它是连续序列的一部分，更新结果数组`result`的对应值，即当前连续长度。 5. 如果元素小于栈顶元素，说明连续序列被打破，将栈顶元素及其索引弹出，直到找到一个较小或相等的元素，或者栈为空。 6. 每次弹出栈顶元素时，都要更新结果数组`result`，因为弹出的元素意味着在当前轮次中找到了一个新的最大连续长度。 7. 继续遍历，直到所有元素都被处理。 8. 最后，遍历结果数组`result`，找到其中的最大值，这个值就是最大子矩阵的面积。 以下是一个简化版的Java代码实现： ```java import java.util.Stack; public class MaxRectangle { public static void main(String[] args) { Integer[] arr = {2, 1, 3, 5, 7, 6, 4}; Integer maxRectangleArea = maxRectangleArea(arr); System.out.println("数组中最大的连续的矩形区域的面积为：" + maxRectangleArea); } private static Integer maxRectangleArea(Integer[] arr) { int[] result = new int[arr.length]; Stack<Integer> stack = new Stack<>(); for (int i = 1; i <= arr.length; i++) { while (!stack.isEmpty() && arr[stack.peek()] >= arr[i]) { result[stack.pop()] = i - 1; } stack.push(i); result[i] = i - (stack.isEmpty() ? 0 : result[stack.peek()]); } return getMaxFromResult(result); } private static Integer getMaxFromResult(int[] result) { int maxArea = 0; for (int area : result) { maxArea = Math.max(maxArea, area); } return maxArea; } } ``` 这段代码中，`maxRectangleArea`函数负责计算最大面积，使用一个栈`stack`来辅助处理连续序列。`getMaxFromResult`函数则用于找出结果数组中的最大值。 这种简便解法虽然可能不如栈解法效率高，但它以较低的复杂度提供了一个易于理解和实现的解决方案，适用于对算法要求不那么严格的场景。在实际编程中，根据问题的具体需求和性能要求，可以选择适合的算法来解决问题。