贝叶斯方法探索：从推断管道到蒙特卡洛模拟

需积分: 9 201 浏览量更新于2024-07-17 收藏 1.45MB PDF 举报

"这是一份关于BAYES METHODS的课程资料，包含18讲内容，由Geoff Nicholls教授及团队提供。课程涵盖了贝叶斯推断的基本流程、马尔科夫链蒙特卡洛方法、模型选择、模型平均以及先验诱导等主题。课程材料包括讲义和问题集，可在指定网站上获取。课程包括16次讲座，并设有辅导课和实践环节。此外，还提供了部分未完成的讲座笔记，用于辅助学习。" 详细知识点： 1. **贝叶斯推断的基本流程** (The Bayesian inferential pipeline): - 在贝叶斯推断中，我们关注的是一个未知的真实世界量Θ，它在某个可能的取值空间Ω中变化。 - 当我们有一个感兴趣的子集S⊆Ω时，可以对事件Θ∈S进行概率评估，比如给出赔率OS。 - 贝叶斯推断的核心在于使用先验概率和观测数据来更新我们的信念，形成后验概率。 - 其流程通常包括：设定先验分布 → 观测数据的收集 → 应用贝叶斯公式 → 得到后验分布 → 结果解释与应用。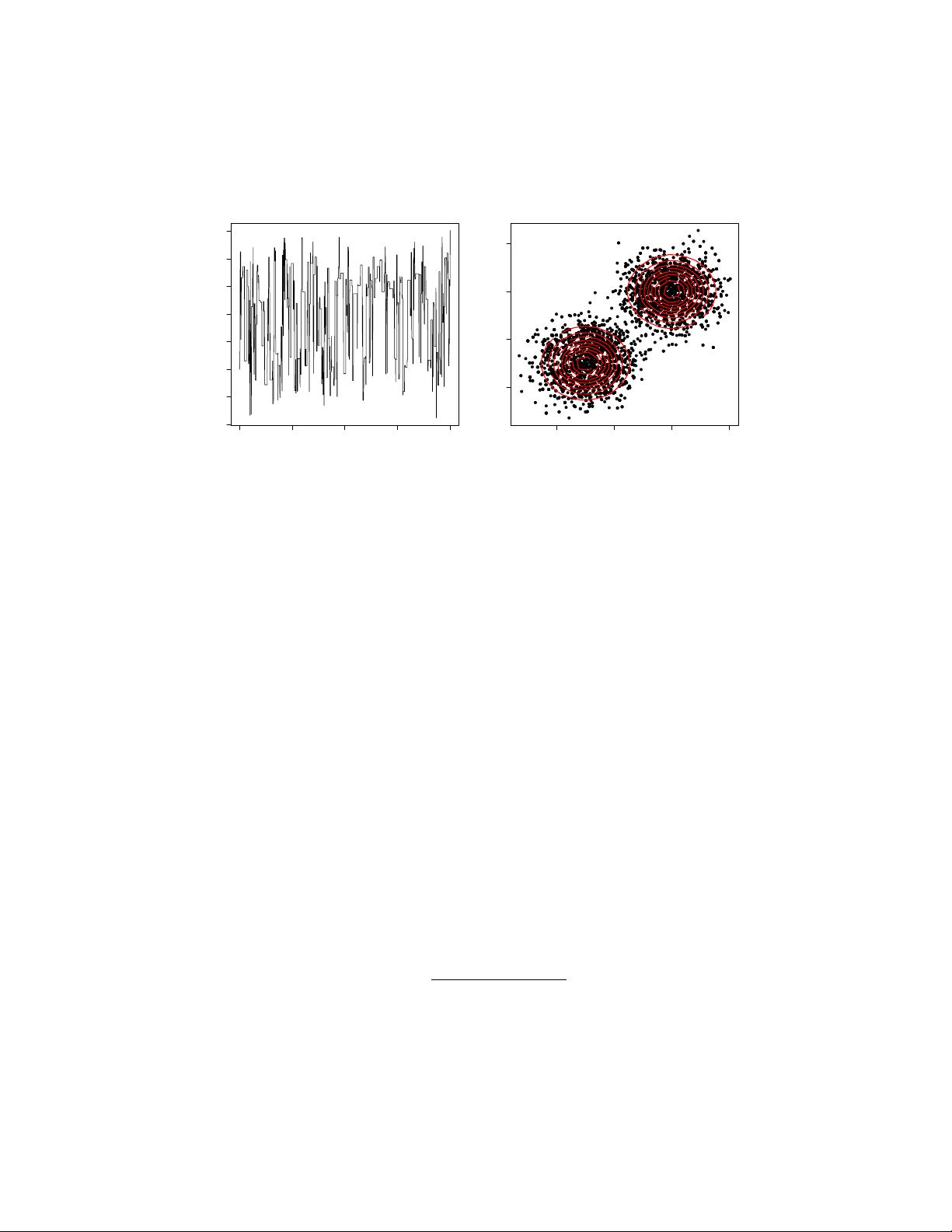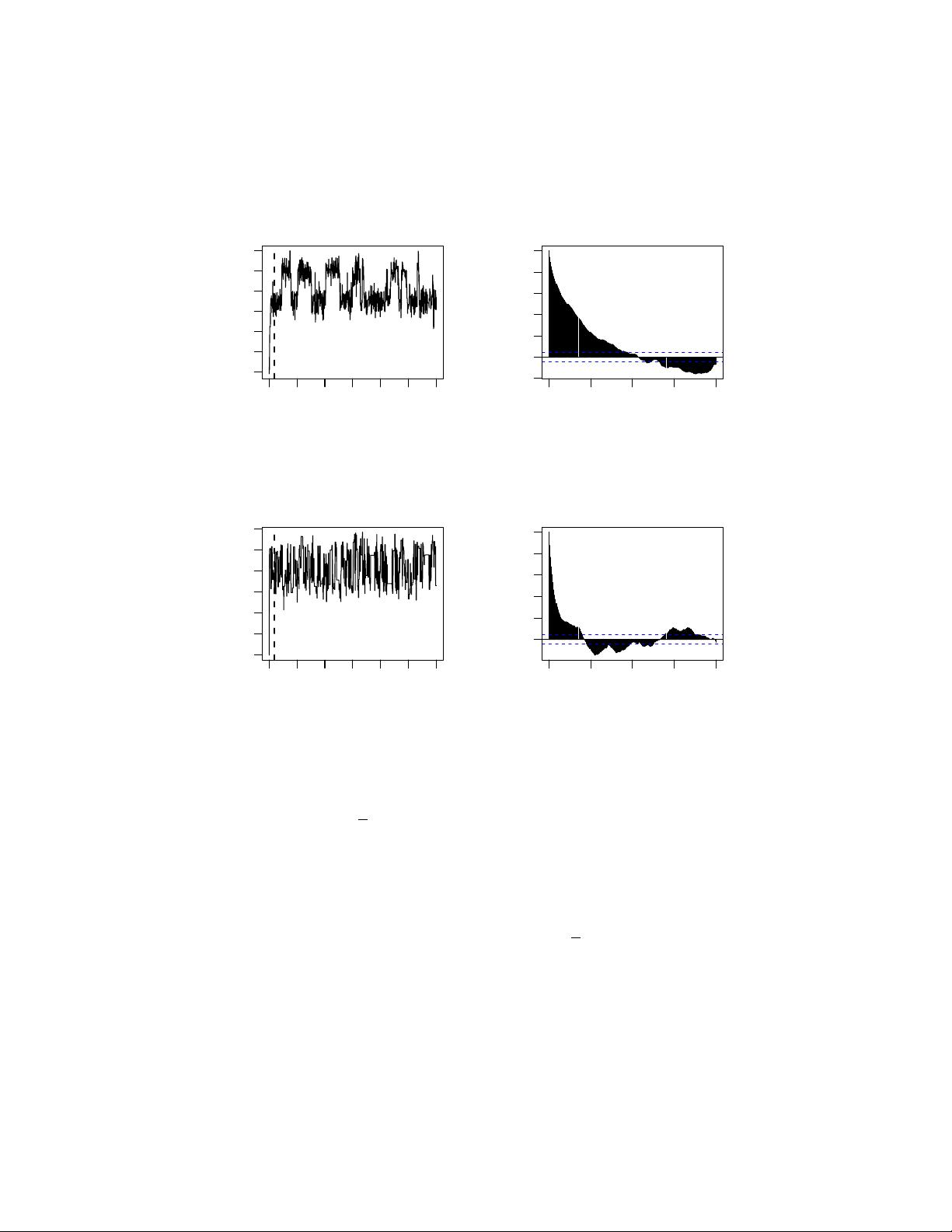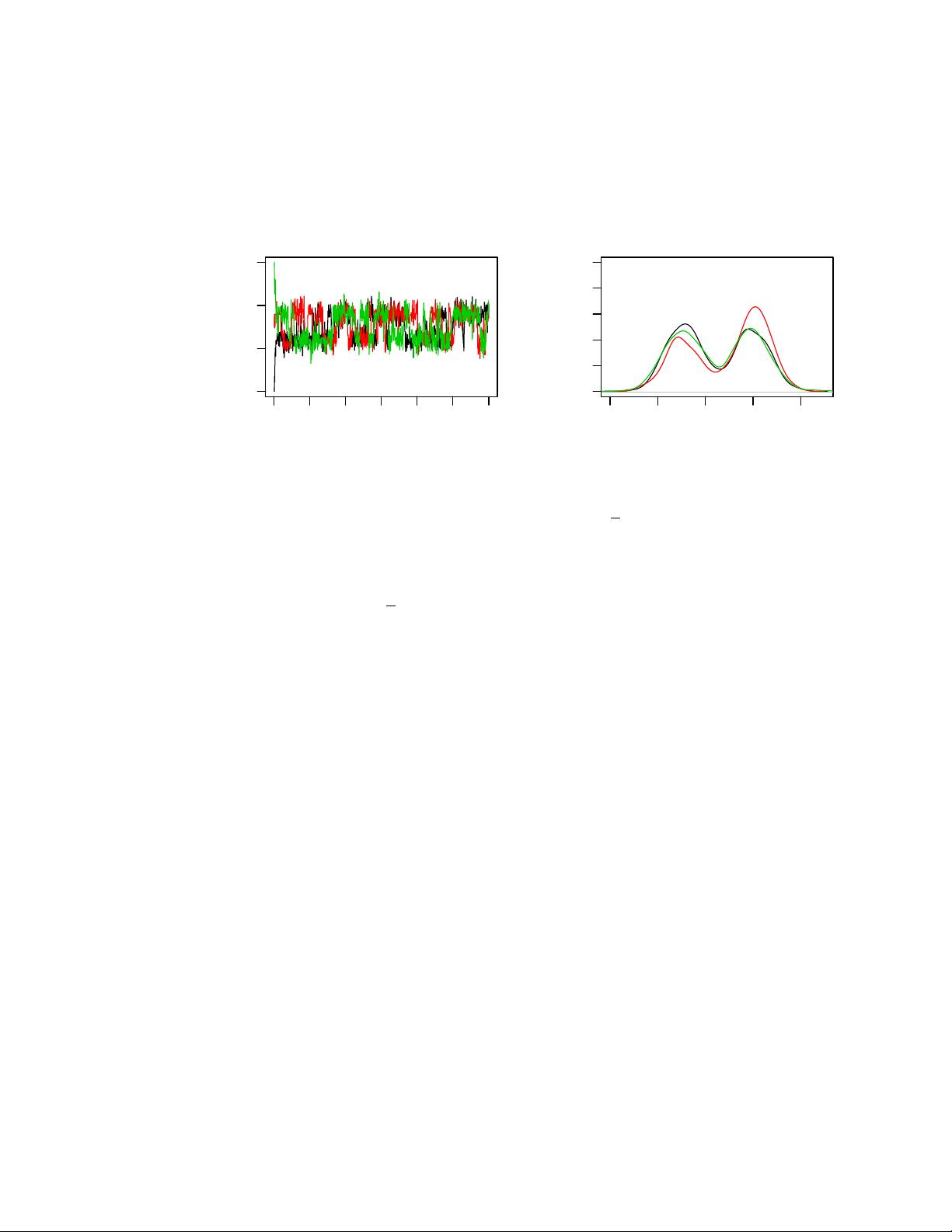 2. **马尔科夫链蒙特卡洛方法** (Markov Chain Monte Carlo, MCMC): - MCMC是一种计算高维概率分布的方法，尤其适用于贝叶斯统计中的复杂后验分布。 - 它通过构造一个马尔科夫链，使得链的平稳分布是目标后验分布，通过链的状态轨迹采样来近似后验分布。 - 常见的MCMC算法有Metropolis-Hastings算法和Gibbs采样。 3. **模型选择** (Model Selection): - 在贝叶斯框架下，模型选择通常涉及到比较不同模型的后验概率或证据。 - 通过计算模型的贝叶斯因子，我们可以评估不同模型对数据的解释能力。 - 模型选择不仅仅是找到最好的模型，还包括理解模型的复杂性与拟合度之间的权衡。 4. **模型平均** (Model Averaging): - 而不是选择单一最佳模型，模型平均考虑了所有模型的贡献，以获得更稳健的预测或估计。 - 这种方法可以减少模型偏差，尤其是在模型不确定性较大时。 5. **先验诱导** (Prior Elicitation): - 先验分布的选择对贝叶斯分析至关重要，因为它反映了我们在观察数据之前的信念。 - 先验诱导涉及如何从专家知识、历史数据或其他来源提取先验信息。 - 正确地指定先验对于确保结果的合理性和可解释性是至关重要的。课程还提供了MSc和Part C类别的课程安排，包括讲座、辅导课和实践，以及一个链接到课程材料的网站。这些资料虽然标注为草稿，但已经包含了从讲座幻灯片整理出的初步内容，尽管还有待完善，如添加图号和说明，调整文本。这些笔记对学生理解和掌握贝叶斯方法提供了宝贵资源。

BAYES METHODS 13

0 500 1000 1500 2000

−1 0 1 2 3 4 5 6

MCMC step t=1,2,3,...

MCMC state X[1]_t

0 2 4 6

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0.45

2.4. Convergence and mixing. We want to estimate E

(f(X)) using our MCMC

samples X

, X

, ..., X

targeting p(x) and calculate the estimate

= n

−1

f(X

The ergodic theorem tells us this estimate converges in probability to E

(f(X)).

How large should we take n? There are two issues.

First, suppose p

(0)

(x) = p(x), so we start the chain in equilibrium. The variance,

var(

), of

will get smaller as n increases. We should choose n large enough to

ensure var(

) is small enough so that

has useful precision. However, calculating

var(

) wont be completely straightforward as the MCMC samples are correlated.

Second, we dont start the chain in equilibrium. The samples in the ﬁrst part of the

chain are biased by the initialization. It is common practice to drop the ﬁrst part

of the MCMC run (called “burn-in”) to reduce the initialization bias. We know

(t)

→ p as → ∞ and want to choose a cut-oﬀ T beyond which p

(t)

' p to a good

approximation. We need n  T so that most of the samples are representative of

Note that if n  T then the bias from burn-in will be slight anyway. One obser-

vation here is that if you need to drop states from the start of the chain to reduce

this bias, you probably havnt run the chain long enough.

The following ﬁgures show autocorrelations for two MCMC runs for the bivariate

normal mixture, with diﬀerent values of the jump size a = 2, 4.

2.4.1. MCMC variance in equilibrium. X

, X

, ... are correlated so var(

) 6=

var(f(X))/n in general.

Correlation at lag s

(f)

cov(f(X

), f(X

i+s

))

var(f(X

))

(so ρ

= 1). Let σ

= var(f(X

)). This doesnt depend on i because the chain is

stationary, because it was started in equilibrium.

Express var(

) in terms of ρ

(f)

. This gives insight and leads to an estimator for

var(

), since we can estimate ρ

(f)

16 GEOFF K NICHOLLS

2.5.1. The Gibbs sampler. The Gibbs sampler is particularly natural. It works

well if we can easily sample conditional distributions. Suppose for eg π(θ

, θ

) is a

bivariate density we want to sample and we have (θ

, θ

) ∼ π.

Simulate a new θ

∼ π(θ

|θ

) and then simulate θ

∼ π(θ

|θ

) (using the new θ

The distribution of (θ

, θ

) is

p(θ

, θ

) =

π(θ

, θ

)π(θ

|θ

)π(θ

|θ

)dθ

dθ

π(θ

, θ

)

π(θ

, θ

)

π(θ

)

π(θ

, θ

)

π(θ

)

dθ

π(θ

|θ

)π(θ

|θ

)π(θ

, θ

)dθ

dθ

= π(θ

, θ

)

π(θ

|θ

)dθ

π(θ

|θ

)dθ

= π(θ

, θ

) since the integrals are each equal one.

so if we start with (θ

, θ

) ∼ π then after these two steps we have a new correlated

sample (θ

, θ

) ∼ π. If θ

(0)

= (θ

, θ

), then θ

(1)

= (θ

, θ

) and we can iterate to

simulate θ

(2)

, θ

(3)

...

The Gibbs sampler comes in several ﬂavors. In the multivariate case θ = (θ

, θ

, ..., θ

)

we can sample π(θ

|θ

−i

) for i = 1, 2, 3, ..., K in turn, or select i ∼ U{1, 2, 3, ..., K}

at each step. We need to check the ergodicity conditions when we construct a new

MCMC sampler.

Exercise: consider a Metropolis Hastings algorithm targeting π(θ

, θ

) with pro-

posal q(θ

|θ) = π(θ

|θ

). Show that the acceptance probability is equal one. Hence

show that the Gibbs sampler is a MH sampler.

2.5.2. Data Augmentation. Some important early applications of the Gibbs sampler

arise in the context of missing data. This is also called “data augmentation”.

DA is convenient when the likelihood on the full data is much simpler than the

likelihood on the observed data.

Suppose the observation process is z ∼ p(z|θ), y ∼ p(y|z, θ) and we observe y. The

posterior p(θ|y) is awkward as the likelihood is an integral,

L(θ; y) =

p(y|z, θ)p(z|θ)dz

In data augmentation we work with the joint posterior density p(θ, z|y), thinking

of the missing data as another parameter. The likelihood is

p(θ, z|y) ∝ p(y|z, θ)p(z|θ)p(θ)

The original DA algorithm was a Gibbs sampler

[1] z

∼ p(z

|θ, y) with p(z

|θ, y) ∝ p(y|z

, θ)p(z

|θ)

[2] θ

∼ p(θ

|y, z

)

2.5.3. Example of DA: Probit regression. In probit regression we have, for the

ith observation y

, i = 1, ..., n, covariates x

= (x

i,1

, ..., x

i,p

), parameters θ =

(θ

, θ

, ..., θ

), a linear predictor η

i,j

, and observation model

∼ Bernoulli(Φ(η

))

with Φ the cdf of a standard normal.

剩余75页未读，继续阅读

咳咳唐

粉丝: 2
资源: 5

贝叶斯方法探索：从推断管道到蒙特卡洛模拟

BAYES METHODS18讲 讲义代码 #数据无法同时上传，见下帖（免费）

BAYES METHODS16讲 讲义数据

BAYES METHODS10讲，讲义数据

BAYES AND EMPIRICAL BAYES METHODS FOR DATA ANALYSIS

Empirical Bayes Methods With Applications,2nd_[Maritz1989]

bayes代码.rar bayes代码实现 Python

bayes

bayes理论的matlab代码

PSD保证下近似贝叶斯推理的Bayes-Newton方法_Bayes-Newton Methods for Approximat

基于Matlab实现Bayes分类器设计（源码+数据）.rar

最新资源

BAYES METHODS18讲讲义代码 #数据无法同时上传，见下帖（免费）

BAYES METHODS16讲讲义数据