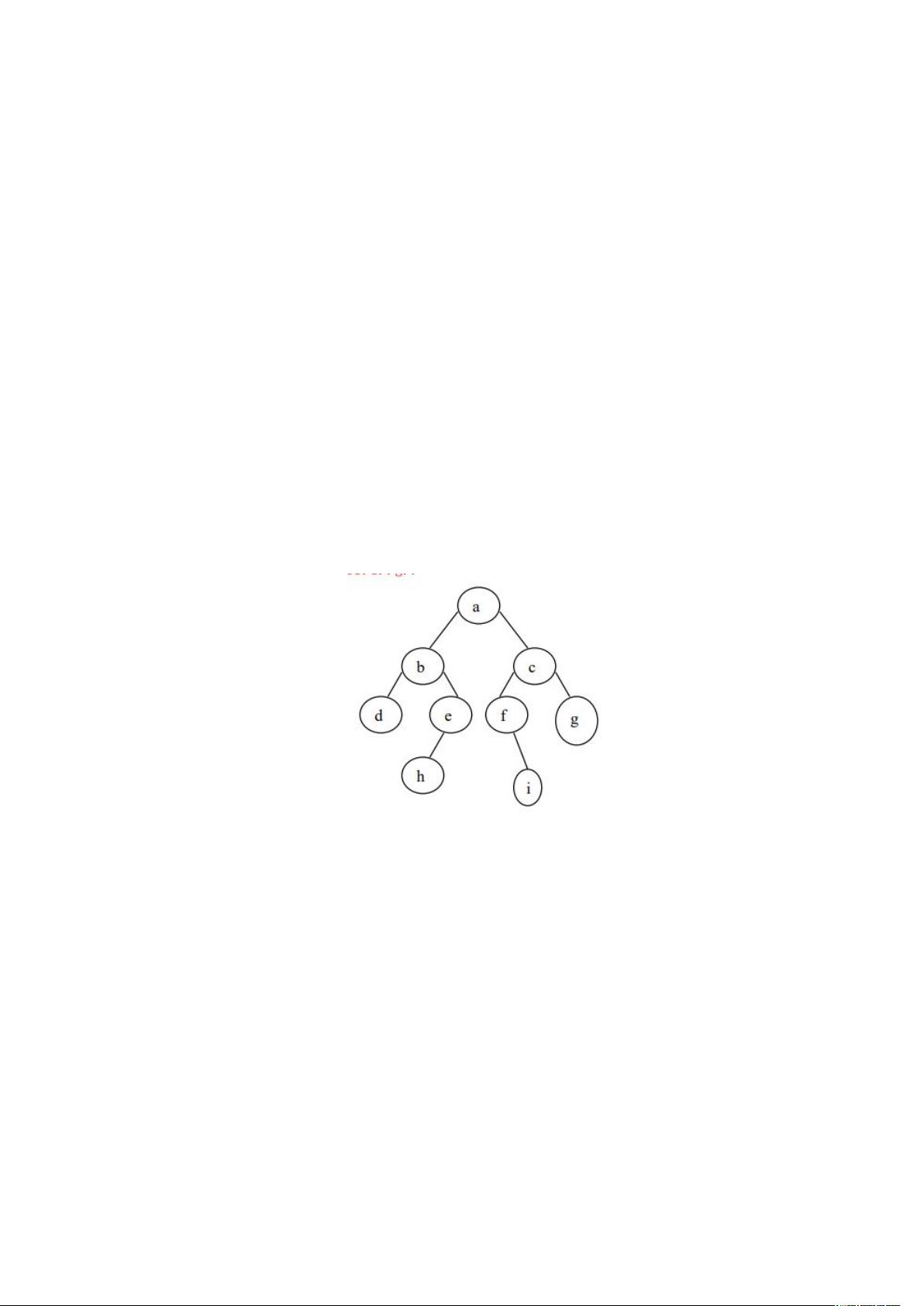
二叉树构造与遍历算法实现

"这篇资料是关于数据结构学习中的二叉树及其应用，主要涉及二叉树的二叉链表存储结构、构造二叉树的方法以及三种遍历方式（先序、中序、后序）的实现。" 在计算机科学中，二叉树是一种基本的数据结构，它由节点（或称为结点）组成，每个节点最多有两个子节点，通常分为左子节点和右子节点。二叉树在很多领域有着广泛的应用，如文件系统、编译器、搜索算法等。本资源的目标是帮助读者熟悉二叉树的二叉链表存储结构，掌握如何根据给定的顺序构建二叉树，并深入理解二叉树的遍历。 二叉链表存储结构是一种常见的二叉树表示方法，每个节点包含三个部分：数据域用于存储节点的数据，左子节点指针指向左孩子，右子节点指针指向右孩子。当某个子节点为空时，对应的指针通常设为NULL。 要根据给定的前根排序序列构造二叉树，可以使用递归的方法。首先读取序列的第一个字符，如果该字符是'.'，则表示当前节点为空；否则，创建一个新节点，将字符作为节点数据，并递归地构造左右子树。示例程序中`createbitree()`函数就是实现这一过程的。 在遍历二叉树时，有三种常用的方法： 1. **先序遍历**：先访问根节点，然后遍历左子树，最后遍历右子树。在程序中，`pretraverse()`函数实现了这个过程，通过递归调用来依次打印根节点、左子树和右子树。 2. **中序遍历**：先遍历左子树，然后访问根节点，最后遍历右子树。这通常用于构造二叉搜索树的排序序列。`inordertraverse()`函数按照此顺序打印节点数据。 3. **后序遍历**：先遍历左子树，然后遍历右子树，最后访问根节点。在后序遍历中，`posttraverse()`函数使用递归先打印左子树和右子树，最后打印根节点。 通过这些操作，我们可以根据输入的前根排序序列构建二叉树，并输出其先序、中序和后序遍历的结果。这种能力对于理解和处理与二叉树相关的各种问题至关重要，比如查找、插入和删除操作等。在实际编程中，了解和掌握二叉树的各种操作是解决复杂问题的基础，特别是对于那些涉及数据组织和搜索效率的问题。