C0G (NP0) AVX 陶瓷电容：温度补偿与性能特性

 ceramic
需积分: 11 0 下载量 27 浏览量 更新于2024-07-18 收藏 569KB PDF 举报
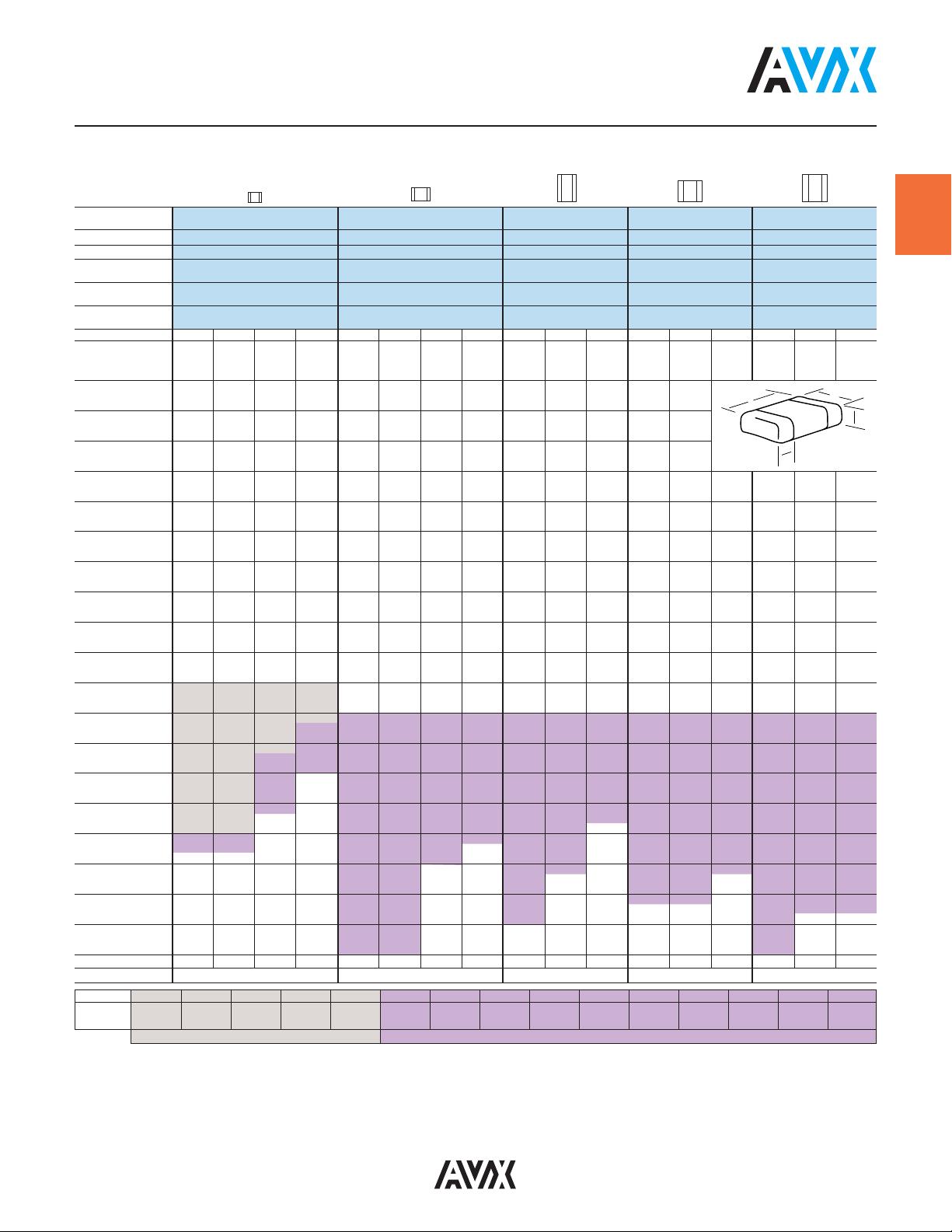
"C0G (NP0) AVX 陶瓷电容是EIA Class I 陶瓷材料中的一种温度补偿配方，广泛应用于电子设备中。这种电容器在现代设计中通常包含钕、钐等元素，以确保其性能稳定。C0G (NP0) 电容的特点是具有极低的电容变化率，典型温度系数为0±30ppm/°C，这意味着在广泛的温度范围内，其电容值保持高度稳定。" 在实际应用中，C0G (NP0) 陶瓷电容的绝缘电阻与温度密切相关，随着温度的升高或降低，绝缘电阻会有所变化。例如，图表显示了在不同温度下，绝缘电阻从100到100,000 Ohm-Farads的变化。这种特性对于在高温或低温环境下工作的电路至关重要，因为它影响了电容的可靠性。 电容器的阻抗与频率之间的关系也是其关键特性之一。从图表中可以看出，C0G (NP0) 电容的阻抗随着频率的增加而增加，这对于高频应用中的滤波和耦合功能有直接影响。不同尺寸的芯片（如1206、0805、1812、1210）表现出不同的阻抗变化，这可能影响它们在特定电路中的适用性。 此外，C0G (NP0) 电容与X7R电容相比，其电容值在频率变化上的稳定性更好。X7R电容在高频下的电容变化率明显高于C0G (NP0)，这表明C0G (NP0) 更适用于对电容稳定性要求严格的场合。 电容值的大小也会影响阻抗随频率的变化。比较10pF、100pF和1000pF的C0G (NP0) 电容，可以看到随着电容值的增大，阻抗在高频下的表现会降低。这意味着在设计电路时，选择合适的电容值可以优化电路的高频响应。 C0G (NP0) 陶瓷电容的一般规格还包括其优秀的温度补偿能力，这使得它在需要精确电容值保持不变的应用中成为首选，如时钟振荡器、电源滤波、数据存储和精密信号处理电路。C0G (NP0) AVX 陶瓷电容因其出色的稳定性、低电容变化率和高绝缘电阻，广泛用于需要高度精确和可靠性的电子系统中。

贴片电容封装指南AVX瓷片电容

2010-05-28 上传
本文档旨在提供关于贴片电容（SMD Capacitors）封装的相关技术指导，特别是针对AVX公司的C0G（NP0）系列瓷片电容器。通过本指南，读者将能够了解到该类型电容器在不同条件下的性能表现及其主要规格参数。 #### 二、...

2021-2022年收藏的精品资料贴片陶瓷电容的NPO、C0G、X7R、X5R、Y5V、Z5U辨析.doc

2021-09-17 上传
C0G电容的温度系数为0ppm/℃，意味着在指定温度范围内，电容值几乎保持不变。这使得C0G电容非常适合在要求高稳定性和低损耗的电路中使用，与NPO电容实际上是一个概念，只是标准不同。 3. **Ⅰ类陶瓷电容器**： Ⅰ...

C语言.np

2022-11-24 上传
C语言.np

AVX多层陶瓷电容失效机理与分析研究

点击了解资源详情
AVX生产的多层陶瓷电容涵盖广泛的产品线，从低电容值的C0G/NP0到高温高容的X7R/X8R，再到高可靠性、高应力条件下的军用和航空航天等级别。研究AVX的产品线可以帮助我们了解特定失效分析案例中涉及的电容类型。 知识...

分析代码def motion_compensate(img, Mvx, Mvy, pel): m, n = np.shape(img)[0], np.shape(img)[1] #读取行数、列数 img = resize(img, (np.int32(m/pel), np.int32(n/pel)), mode = 'reflect' ) Blocksize = np.floor(np.shape(img)[0]/np.shape(Mvx)[0]) m, n = np.shape(img)[0], np.shape(img)[1] M, N = np.int32(np.ceil(m/Blocksize)*Blocksize), np.int32(np.ceil(n/Blocksize)*Blocksize) f = img[0:M, 0:N] Mvxmap = resize(Mvy, (N,M)) Mvymap = resize(Mvx, (N,M)) xgrid, ygrid = np.meshgrid(np.arange(0,N-0.99), np.arange(0,M-0.99)) X = np.clip(xgrid+np.round(Mvxmap/pel),0,N-1) Y = np.clip(ygrid+np.round(Mvymap/pel),0,M-1) idx = np.int32(Y.flatten()*N + X.flatten()) f_vec = f.flatten() g = np.reshape(f_vec[idx],[N,M]) g = resize(g, (np.shape(g)[0]*pel,np.shape(g)[1]*pel)) return g

2023-06-08 上传
10. 对g进行上采样，并返回结果g。 这段代码的作用是对输入的图像进行运动补偿处理，通过运动矢量Mvx和Mvy计算出图像中块的新位置，从而得到补偿后的图像。其中，运动矢量的大小决定了块的大小，而下采样和上采样则...

翻译代码import numpy as np from cvxopt import matrix, solvers solvers.options['show_progress'] = False # 市场出清，考虑网络阻塞 def market_clearing(alpha): # 供给曲线的截距和斜率 a_real = np.array([15.0, 18.0]) b_real = np.array([0.01, 0.008]) # 需求曲线的截距和斜率 c_real = np.array([40.0, 40.0]) * -1 d_real = np.array([0.08, 0.06]) # 机组功率上下限 p_min = np.array([0.0, 0.0]) p_max = np.array([500.0, 500.0]) # 负荷需求上下限 q_min = np.zeros(2) q_max = np.array([500.0, 666.666666666667]) J_g = ([[-0.333333333333333, -0.333333333333333, -0.666666666666667], [0.333333333333334, -0.666666666666667, -0.333333333333333], [0, 0, 0]]) J = np.array([[-0.333333333333333, 0.0, 0.333333333333333, -0.333333333333334], [-0.333333333333333, 0.0, 0.333333333333333, 0.666666666666667], [-0.666666666666667, 0.0, 0.666666666666667, 0.333333333333333]]) J_max = np.array([25.0, 1000.0, 1000.0, 25.0, 1000.0, 1000.0]) P = matrix(np.diag(np.append(b_real, d_real))) q = matrix(np.append(alpha, c_real)) G = matrix(np.vstack((J, -J, np.diag(-np.ones(4)), np.diag(np.ones(4))))) h = matrix(np.hstack((J_max, -p_min, -q_min, p_max, q_max))) A = matrix(np.hstack((-np.ones(2), np.ones(2)))).T b = matrix(0.0) sv = solvers.qp(P, q, G, h, A, b) miu1 = sv['z'][0:3] miu2 = sv['z'][3:6] nodal_price = (np.ones((3, 1)) * sv['y'][0] - np.dot(J_g, miu1 - miu2)).squeeze() nodal_price_g = np.array([nodal_price[0], nodal_price[2]]) mc_amount = np.array(sv['x'][:2]).squeeze() cost_real = 0.5 * b_real * mc_amount ** 2 + a_real * mc_amount cost_declare = mc_amount * np.transpose(nodal_price_g) profit = cost_declare - cost_real return nodal_price_g, profit if __name__ == '__main__': alpha = np.array([20.29, 22.98]) print(market_clearing(alpha))

2023-06-06 上传
- c_real和d_real：表示需求曲线的截距和斜率，同样是一个长度为2的数组。 - p_min和p_max：表示机组功率的上下限，也是一个长度为2的数组。 - q_min和q_max：表示负荷需求的上下限，同样是一个长度为2的数组。 - J_...

def auto_whiteBalance(img): b, g, r = cv2.split(img) Y = 0.299 * r + 0.587 * g + 0.114 * b Cr = 0.5 * r - 0.419 * g - 0.081 * b Cb = -0.169 * r - 0.331 * g + 0.5 * b Mr = np.mean(Cr) Mb = np.mean(Cb) Dr = np.var(Cr) Db = np.var(Cb) temp_arry = (np.abs(Cb - (Mb + Db * np.sign(Mb))) < 1.5 * Db) & ( np.abs(Cr - (1.5 * Mr + Dr * np.sign(Mr))) < 1.5 * Dr) RL = Y * temp_arry # 选取候选白点数的最亮10%确定为最终白点，并选择其前10%中的最小亮度值 # L_list = list(np.reshape(RL, (RL.shape[0] * RL.shape[1],)).astype(np.int)) L_list = list(np.reshape(RL, (RL.shape[0] * RL.shape[1],)).astype(int)) hist_list = np.zeros(256) min_val = 0 sum = 0 for val in L_list: hist_list[val] += 1 for l_val in range(255, 0, -1): sum += hist_list[l_val] if sum >= len(L_list) * 0.1: min_val = l_val break # 取最亮的前10%为最终的白点 white_index = RL < min_val RL[white_index] = 0 # 计算选取为白点的每个通道的增益 b[white_index] = 0 g[white_index] = 0 r[white_index] = 0 Y_max = np.max(RL) b_gain = Y_max / (np.sum(b) / np.sum(b > 0)) g_gain = Y_max / (np.sum(g) / np.sum(g > 0)) r_gain = Y_max / (np.sum(r) / np.sum(r > 0)) b, g, r = cv2.split(img) b = b * b_gain g = g * g_gain r = r * r_gain # 溢出处理 b[b > 255] = 255 g[g > 255] = 255 r[r > 255] = 255 res_img = cv2.merge((b, g, r)) return res_img

2023-07-15 上传
感谢提供代码。根据您的代码，问题可能出现在加载图像数据的部分。请确保您正确地加载了图像数据，并且可以通过`cv2.imshow()`函数显示图像。如果您遇到了无法加载图像数据的问题，请尝试检查图像路径是否正确，并...

import numpy as np import matplotlib.pyplot as plt import sympy from scipy.interpolate import interp1d gamma = 1.2 R = 8.314 T0 = 500 Q = 50 * R * T0 a0 = np.sqrt(gamma * R * T0) M0 = 6.216 P_P0 = sympy.symbols('P_P0') num = 81 x0 = np.linspace(0,1,num) t_t0 = np.linspace(0,15,num) x = x0[1:] T_T0 = t_t0[1:] h0 = [] h1 = []#创建拉姆达为1的空数组 r = [] t = [] c = [] s = [] i = 0 for V_V0 in x: n1 = sympy.solve(1 / (gamma-1) * (P_P0 * V_V0 - 1) - 0.5 * (P_P0 + 1) * (1 - V_V0)- gamma * 0 * Q / a0 ** 2,P_P0)#lamuda=0的Hugoniot曲线方程 n2 = sympy.solve(1 / (gamma-1) * (P_P0 * V_V0 - 1) - 0.5 * (P_P0 + 1) * (1 - V_V0)- gamma * 1 * Q / a0 ** 2,P_P0)#lamuda=1的Hugoniot曲线方程 n3 = sympy.solve(-1 * P_P0 + 1 - gamma * M0 ** 2 * (V_V0 - 1),P_P0)#Reyleigh曲线方程 n4 = 12.014556 / V_V0#等温线 n5 = sympy.solve((P_P0 - 1 / (gamma+1) )* (V_V0-gamma / (gamma + 1)) - gamma / ((gamma + 1) ** 2),P_P0)#声速线 n6 = 10.6677 / np.power(V_V0,1.2)#等熵线 h0.append(n1) h1.append(n2) r.append(n3) t.append(n4) c.append(n5) s.append(n6) i = i+1 h0 = np.array(h0) h1 = np.array(h1) r = np.array(r) t = np.array(t) c = np.array(c) s = np.array(s) plt.plot(x,r,label='Rayleigh') plt.plot(x,t,color='purple',label='isothermal') plt.plot(x,s,color='skyblue',label='isentropic') a = np.where(h0 < 0) b = np.where(c < 0) h0 = np.delete(h0,np.where(h0 < 0)[0],axis = 0)#去除解小于0的值 h1 = np.delete(h1,np.where(h1 < 0)[0],axis = 0)#去除解小于0的值 c = np.delete(c,np.where(c < 0)[0],axis = 0)#去除解小于0的值 x0 = np.delete(x,a,axis = 0)#对应去除x轴上错误值的坐标 x1 = np.delete(x,b,axis = 0) plt.plot(x0,h0,label='Hugoniot(lambda=0)') plt.plot(x0,h1,label='Hugoniot(lambda=1)') plt.plot(x1,c,color='yellow',label='soniclocus') plt.ylim((0,50)) plt.legend() # 显示图例 plt.xlabel('V/V0') plt.ylabel('P/P0') f1 = interp1d(x1, c.T, kind='cubic') f2 = interp1d(x,r.T,kind='cubic') f3 = interp1d(x, t.T, kind='cubic') epsilon = 0.0001 x0 = 0.56 y0 = f1(x0) - f2(x0) while abs(y0) > epsilon: df = (f1(x0 + epsilon) - f2(x0 + epsilon) - y0) / epsilon x0 -= y0 / df y0 = f1(x0) - f2(x0) plt.scatter(x0, y0, 50, color ='red') plt.show()

2023-06-08 上传
这是一个 Python 代码，我可以解读出来。这段代码主要是用来绘制气体动力学中的一些...这段代码还包括了一些数据处理的操作，比如删除数组中小于0的值、插值等等。最后，这段代码还用牛顿迭代法求解了两条曲线的交点。

np.array(0) / np.array(0) np.array(0) // np.array(0) np.array([np.nan]).astype(int).astype(float)

2024-09-09 上传
1. `np.array(0) / np.array(0)`：这里创建了两个包含单个元素0的数组，并尝试对它们进行除法操作。由于数学上任何数除以0都是未定义的，所以这个操作的结果会抛出一个`RuntimeWarning`警告，并且返回一个包含`NaN`...

def drawGaussian(img, pt, score, sigma=1): tmp_img = np.zeros([img.shape[0], img.shape[1]], dtype=np.float32) tmpSize = 3 * sigma # Check that any part of the gaussian is in-bounds ul = [int(pt[0] - tmpSize), int(pt[1] - tmpSize)] br = [int(pt[0] + tmpSize + 1), int(pt[1] + tmpSize + 1)] if (ul[0] >= img.shape[1] or ul[1] >= img.shape[0] or br[0] < 0 or br[1] < 0): # If not, just return the image as is return img # Generate gaussian size = 2 * tmpSize + 1 x = np.arange(0, size, 1, float) y = x[:, np.newaxis] x0 = y0 = size // 2 # Usable gaussian range g_x = max(0, -ul[0]), min(br[0], img.shape[1]) - ul[0] g_y = max(0, -ul[1]), min(br[1], img.shape[0]) - ul[1] img_x = max(0, ul[0]), min(br[0], img.shape[1]) img_y = max(0, ul[1]), min(br[1], img.shape[0]) g = np.exp(- ((x - x0) ** 2 + (y - y0) ** 2) / (2 * sigma ** 2)) * score g = g[g_y[0]:g_y[1], g_x[0]:g_x[1]] tmp_img[img_y[0]:img_y[1], img_x[0]:img_x[1]] = g img += tmp_img

2023-06-13 上传
这段代码实现了一个在图像上画高斯分布的函数。具体来说，它接受一个图像 `img`、一个中心点坐标 `pt`、高斯分布的得分 `score` 和标准差 `sigma` 作为输入。函数会在图像上生成一个以 `pt` 为中心，标准差为 `sigma...
pctanyicheng
  • 粉丝: 2
  • 资源: 19
上传资源 快速赚钱

最新资源