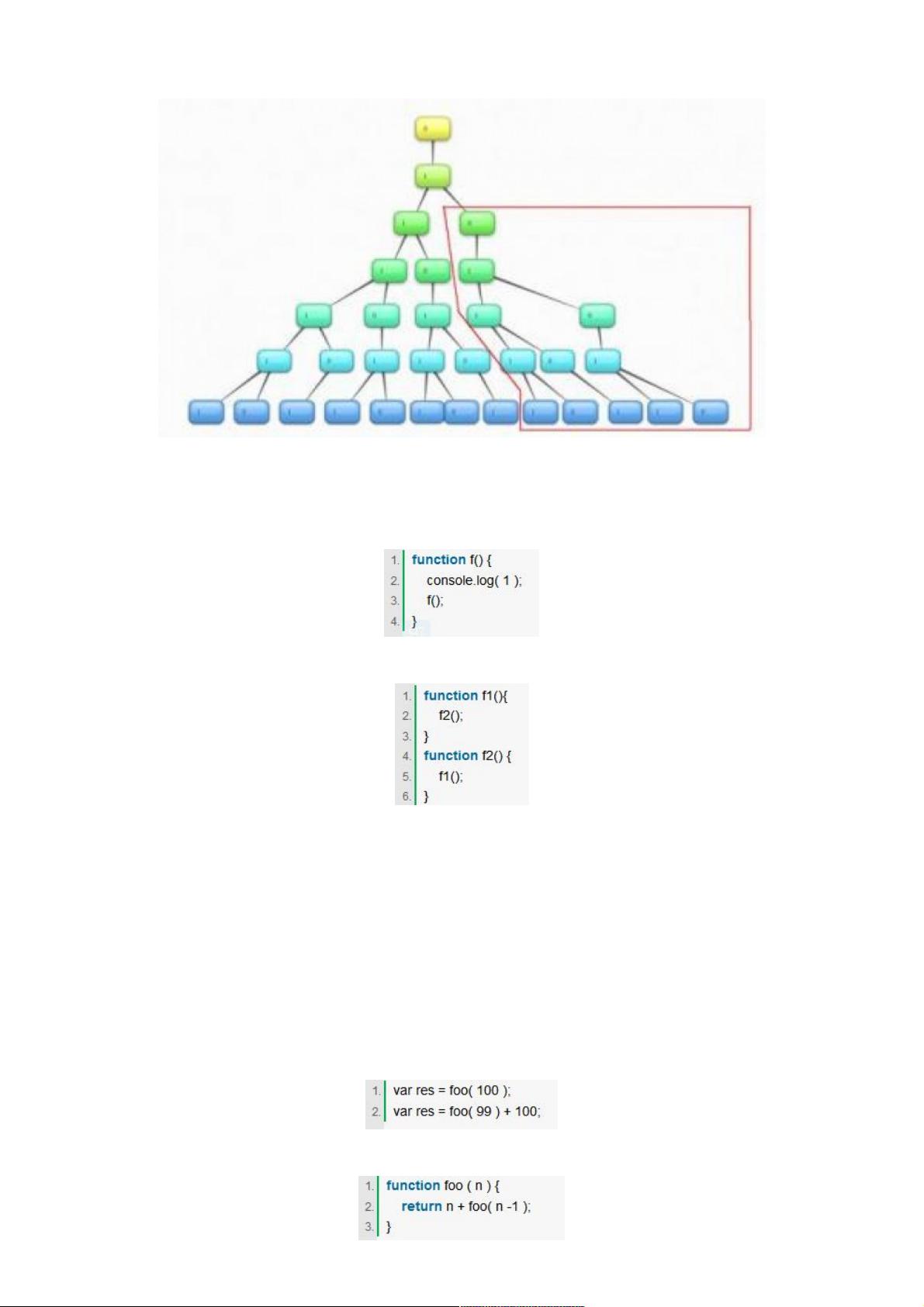
JavaScript进阶：递归原理与数列求解实例

在进阶JavaScript编程中，递归是一种强大的技术，它涉及到函数直接或间接地调用自身来解决问题。递归的关键在于理解如何设置正确的终止条件（也称为“基础案例”或“递归结束条件”），以及如何通过递推关系将问题逐步缩小直至达到这个终止条件。在本篇内容中，我们将深入探讨递归的原理和应用实例。 1. **递归定义**: - 直接调用：函数调用自身即是直接递归，如`foo(n)`调用`foo(n-1)`。 - 间接调用：通过中间变量间接实现，比如使用循环结构实现递归效果。 2. **递归的本质**: - 递归是化归思想的应用，通过将复杂问题分解为更小的同类问题来解决。 - 写递归函数时，问题会被转化为同一函数的不同调用形式，直到问题简化到可以直接处理的简单情况。 3. **累加数列示例**: - 例如计算1到100的累加和，可以通过递归定义`foo(n)`为`n + foo(n-1)`，并设置基础案例`foo(1) = 1`，然后逐次将问题规模减小，直到`n = 1`。 4. **递归求解过程**: - 对于等差数列： - 第n项的递推关系通常是`fn(n) = f(n-1) + 常数`，例如1,3,5,7,9...的递推关系为`fn(n) = fn(n-1) + 2`。 - 求前n项和的递归体为`sum(n) = fn(n) + sum(n-1)`，其中`sum(1) = 1`。 - 对于差分数列，如Fibonacci数列，递推关系是相邻两项的差，如`fn(n) = fn(n-1) + fn(n-2)`，初始项可能为`fn(0) = 1`，`fn(1) = 1`。 5. **临界条件的重要性**: - 递归必须有一个明确的终止条件，否则会陷入无限循环。在上述例子中，这些终止条件通常是n等于某个特定值，如1或0。 6. **实际应用**: - 递归在编程中广泛用于搜索算法（如深度优先搜索），树和图的遍历，以及数学问题如阶乘、排列组合等。 熟练掌握递归技巧是进阶JavaScript编程的关键，它能帮助解决许多复杂问题，并提升代码的简洁性和可读性。在实践中，需要不断理解和练习递归的运用，同时注意优化递归过程以防止性能问题。通过递归，我们可以优雅地解决各种数列问题和结构化问题，增强编程能力。