使用高斯过程回归的HEVC三维全息图像编码方案
121 浏览量
更新于2024-08-31
收藏 1.42MB PDF 举报
"3D全息图像编码方案利用HEVC与高斯过程回归进行3D全息图像编码的研究论文"
本文主要探讨了一种基于高斯过程回归（Gaussian Process Regression, GPR）的3D全息图像编码策略，旨在解决3D全息图像由于其自然且无疲劳的3D可视化特性而带来的大量数据需求问题。全息图像，又称集成成像、光场成像或全光谱成像，能够提供一种逼真的三维视图，但同时也需要大量的数据来表示其丰富的三维内容。因此，开发针对这种特定类型图像的高效编码方案显得至关重要。
该论文提出了一种利用高斯过程回归的预测方法来压缩3D全息图像。在提出的编码方案中，编码块及其预测被用来减少数据量。高斯过程回归是一种统计建模技术，它能用于非线性预测，通过考虑输入数据之间的相关性来估计未知函数。在3D全息图像编码中，这种方法可以预测编码块的未来值，从而减少需要传输的数据量，提高压缩效率。
在论文中，作者可能详细分析了如何将高斯过程回归应用于3D全息图像的预测过程中，包括如何构建合适的特征向量、选择合适的核函数以及优化预测模型的参数。他们可能还探讨了预测误差的处理和如何结合HEVC（High Efficiency Video Coding，高效视频编码）标准来实现更高效的编码。
HEVC是目前最先进的视频编码标准，能够显著提高压缩效率，降低带宽需求，同时保持良好的图像质量。在3D全息图像编码中，HEVC可能被用来处理预测后的残差，进一步压缩数据。结合高斯过程回归的预测能力，这种编码策略有可能实现对3D全息图像的高质量、低延迟的编码和传输。
论文可能会涉及以下方面：
1. 高斯过程回归的基本原理和在图像编码中的应用。
2. 3D全息图像的特点及数据量挑战。
3. 提出的预测模型的构建和优化过程。
4. 如何结合HEVC编码标准实现高效压缩。
5. 实验设计和结果分析，包括与其他编码方法的性能比较。
6. 对未来研究的讨论和展望。
通过这种创新的编码策略，研究人员期望能够在保持图像质量的同时，大幅度减小3D全息图像的存储和传输需求，为3D显示技术的广泛应用铺平道路。
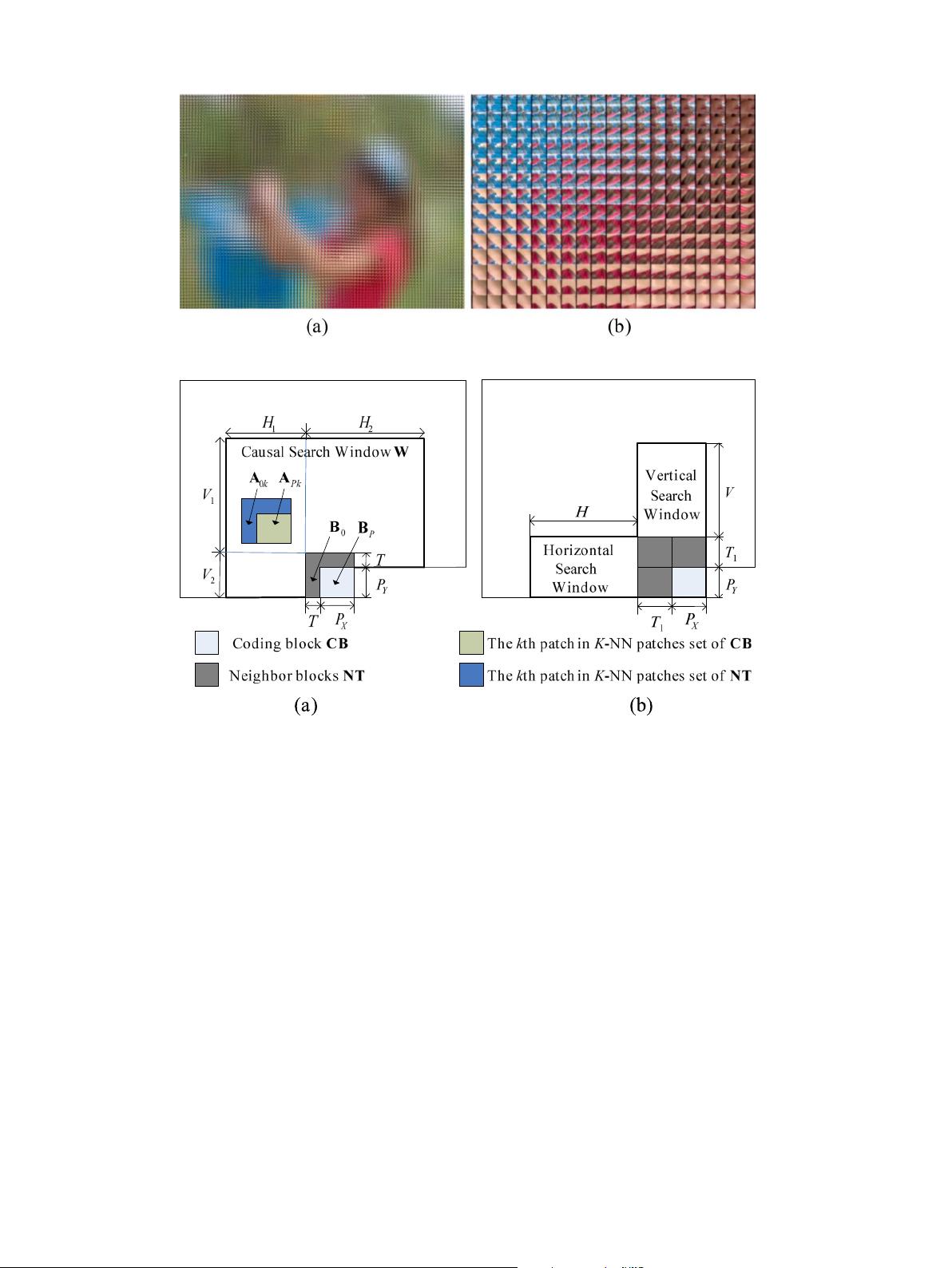
prediction supports. In general, a larger template region can in-
crease the matching accuracy. Therefore, the template region with
thickness being set to
T
1
is used in the searching process, shown in
Fig. 3(b). In this paper, the
T
1
equals to the size of the current
coding block. The next subsection gives the details of the process
to derive the prediction supports.
2.2. Derive the prediction supports
Suppose the region S consists of current coding block CB and its
neighbor template NT, as shown in Fig. 2(b). Let each coding block
be comprised of
×nn
pixels. Hence, region S is of size
=Nn4
2
pixels. The principle of acquiring the prediction supports (K-NN
patches) of the coding block is to first search for K-nearest ap-
proximates of the NT in horizontal and vertical search windows
under Euclidean distance and then obtain the K-NN patches of CB
according to the K-nearest approximates of NT.
Let the N sample values be stacked in a column vector
B
, which
is compacted in a vector
B
0
of 3 n
2
known pixels and a vector
B
P
of
n
2
unknown pixels. Let C denote a so-called dictionary represented
by a matrix of dimension
×NM
, which means all the possible
patches that have the same geometric shape as region S in given
horizontal and vertical searching windows. M here means the total
number of the possible patches in the searching windows. Con-
sequently, the dictionary matrix can also be assumed to be formed
by two submatrices
C
0
of size
×n
M3
2
and
C
P
of size
×n
M
2
,
respectively, corresponding to the spatial location of NT and CB.
The details of acquiring the prediction supports are as follows.
1) Derive vector
B
0
and submatrix
C
0
. Record the indexes of each
atom
c
m0
(i.e., stacked in the mth column of
C
0
) in submatrix
C
0
.
2) Compute Euclidean distance
D
m
between
B
0
and each atom
c
m0
,
based on the following equation:
=‖ − ‖
()
D Bc
1
mm002
2
3) Derive K-NN set
A
0
of NT. Here,
A
0
is composed by the top K
atoms of submatrix
C
0
, which minimize
D
m
. Record the indexes
of these selected atoms in
C
0
.
4) Generate the prediction supports
A
P
of the current coding block
CB, composed by the K atoms of submatrix
C
P
according to the
recorded indexes of the selected atoms in
C
0
.
2.3. Filtrate the prediction supports
The 3D holoscopic image is composed of numerous EIs, which
is quite different from the natural 2D images. The texture homo-
geneous areas hardly prevail in 3D holoscopic image. Since Eu-
clidean distance is not a reasonable matching criterion for edges
and texture regions [22], it is essential to design a filtration
method to ensure that the selected prediction supports are all
approximate to current coding block. In this paper, a filtration
method is put forward, in which NCC [23] is selected as the
Fig. 2. Holoscopic image captured by microlens array: (a) full image; (b) enlargement of the holoscopic image showing the EIs.
Reconstruction blocks
Reconstruction blocks
Fig. 3. Searching windows: (a) a full causal searching window W; (b) specifi ed searching windows in horizontal and vertical directions.
D. Liu et al. / Signal Processing: Image Communication 47 (2016) 438–451440
剩余13页未读，继续阅读
点击了解资源详情
点击了解资源详情
点击了解资源详情
2013-07-25 上传
2013-11-12 上传
2021-02-07 上传
2013-07-25 上传
2021-02-10 上传
2019-06-24 上传
weixin_38674409
- 粉丝: 7
- 资源: 920
我的内容管理
展开
