多自主水下机器人路径规划与编队控制综述

需积分: 9 185 浏览量更新于2024-07-09 收藏 1.76MB PDF 举报

"这篇论文回顾了多自主水下车辆（AUV）的路径规划和编队控制技术。路径规划和编队控制是多车辆系统，尤其是AUV中的关键概念，它们的合作实施能实现期望的结果并提高任务成功的概率。由于AUV的非线性动力学和环境条件，其协同控制是一项挑战。尽管AUV应用的发展表明路径规划和编队控制研究的重要性，但与地面或空中自主车辆相比，这一领域的关注度相对较低，需要进一步探索。论文审查了AUV编队控制的不同结构，并讨论了其优点和挑战。" 在多自主水下车辆（AUV）领域，路径规划和编队控制是两个至关重要的技术。路径规划涉及如何设计和优化AUV的运动轨迹，使其能够有效地从起点到达终点，同时避免碰撞、障碍物以及考虑水下环境的影响，如水流、海底地形等。这通常需要高级的算法，如Dijkstra算法、A*搜索算法或者遗传算法等，以确保路径的有效性和安全性。编队控制则关注多个AUV如何协同工作，形成特定的几何形状或阵型，以执行复杂的任务，如海洋调查、搜救操作或海底构造测绘。编队控制的优势在于可以扩展单个AUV的能力，通过合作完成个体难以达成的目标。编队策略包括集中式、分布式和混合式，每种都有其独特的优势和适用场景。集中式方法依赖一个中心控制器来协调所有AUV的动作，而分布式方法则允许每个AUV根据本地信息做出决策，更加鲁棒但可能复杂度较高。混合式策略结合了两者的优点，适用于大规模AUV群体的控制。尽管AUV的路径规划和编队控制已经取得了一定的进步，但仍然面临诸多挑战。非线性动力学使得AUV的动态模型复杂，需要高级控制理论，如滑模控制、自适应控制等来处理。此外，水下通信的限制，如低带宽、高延迟和易受干扰，对协同控制提出了额外的难题。环境不确定性，如不可预测的水流和海洋条件，也增加了路径规划和编队控制的难度。这篇论文通过回顾现有的研究成果，强调了在AUV领域进一步研究和开发路径规划和编队控制技术的必要性。未来的重点可能包括开发更高效、适应性强的路径规划算法，改进编队控制策略以应对不确定性和通信限制，以及融合感知、决策和控制的集成解决方案，以提高AUV在复杂海洋环境中的自主性和任务完成能力。

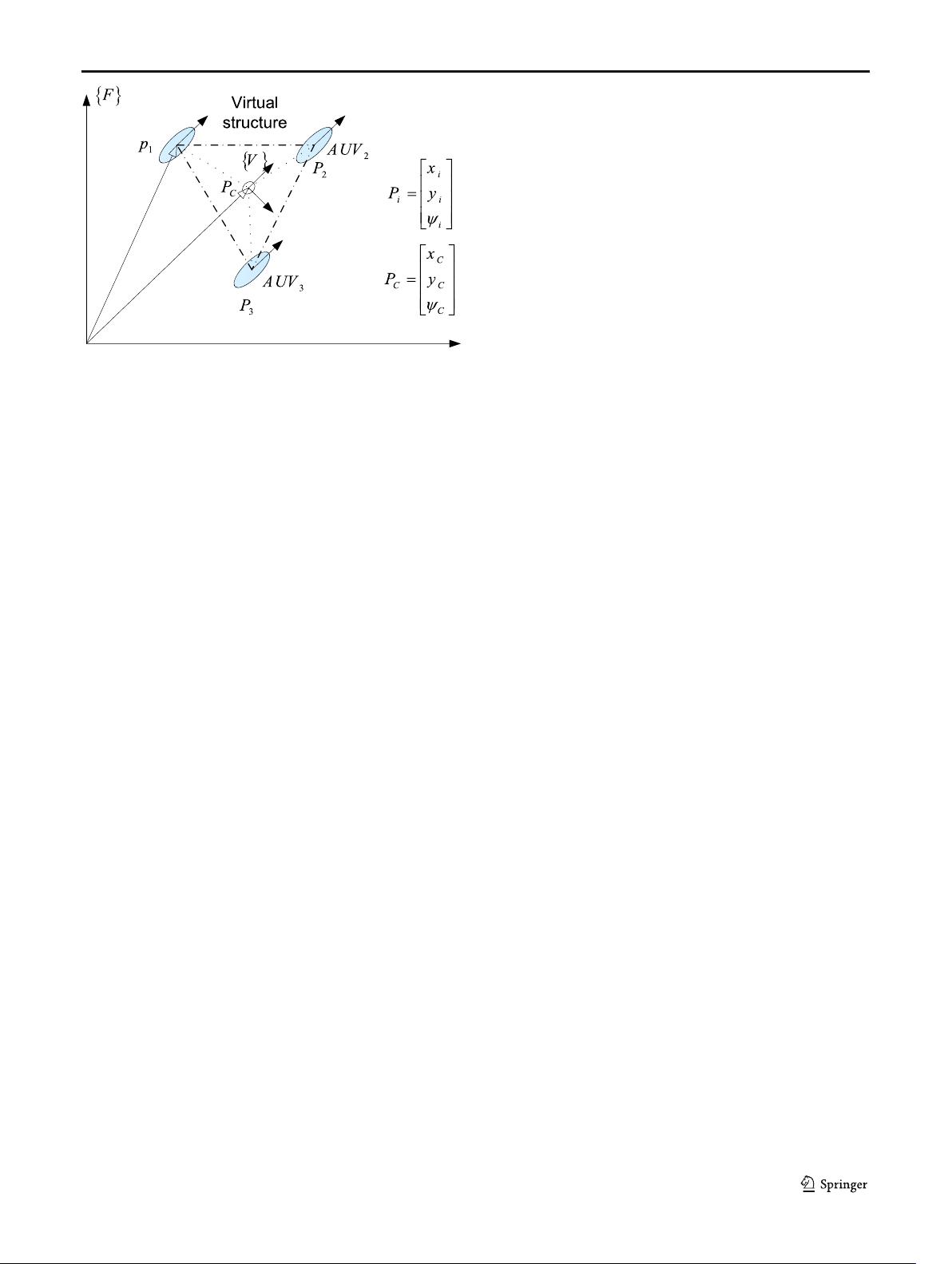
considered equal to the number of AUVs and one-

to-one correspond ence is established between

them. The desired formation is obtained by mini-

mizing the position error function, which is defined

based on the current position of the AUVs and their

desired position in the virtual structure.

Stepe 2: Converting the virtual structure’s desired motion

into desired commands for each of the AUVs in

the group: Having adjusted the desired virtual

structure, a virtual force is applied to the virtual

structure so that the structure can be moved to the

next point. In this section, the vehicle’smotionca-

pacity is taken into consideration.

Stepe 3: Designing an individual tracking controller for each

of the AUVs: After transferring the virtual structure

to the new position (done in Step 2), the control

inputs for each vehicle are designed in such a way

that the vehicle moves to its new corresponding

point in the virtual structure. A simple way for the

movement of vehicles to the desired position is

changing direction towards the desired position

and then transferring to the target point.

Virtual structure is usually used for formation control in

mobile robots, spacecraft [42–44] or small satellites [11,

45–47]. The employment of virtual structure approac h in

spacecraft formation control was presented in [48], where for-

mation feedback from the spacecraft to the virtual structure

was consulted. This would give robustness to the structure of

formation against internal or external disturbances and lead to

better performance. The control strategies of the distributed

virtual structure along with the corresponding coupling of

single-wheeled mobile robots are introduced in [49]. The cor-

responding coupling would create a trade-off between ensur-

ing the tracking of each robot’s desired trajectories and main-

taining the shape of the formation when faced with

disturbances, which can result in higher robustness of the pro-

posed formation structure. The exponential stability of the

dynamics of formation error is proven and the proposed con-

trol design is practically applied. In [50], the two-layer distrib-

uted formation learning control was presented for one group

of AUVs, which included an adaptive distributed observer in

the upper layer and a decentralized deterministic learning con-

troller in the lower layer. The upper layer estimates the virtual

leader’s states and dynamics. The formation tracking control

and learning performance of the neural network with local

information are done in the lower layer.

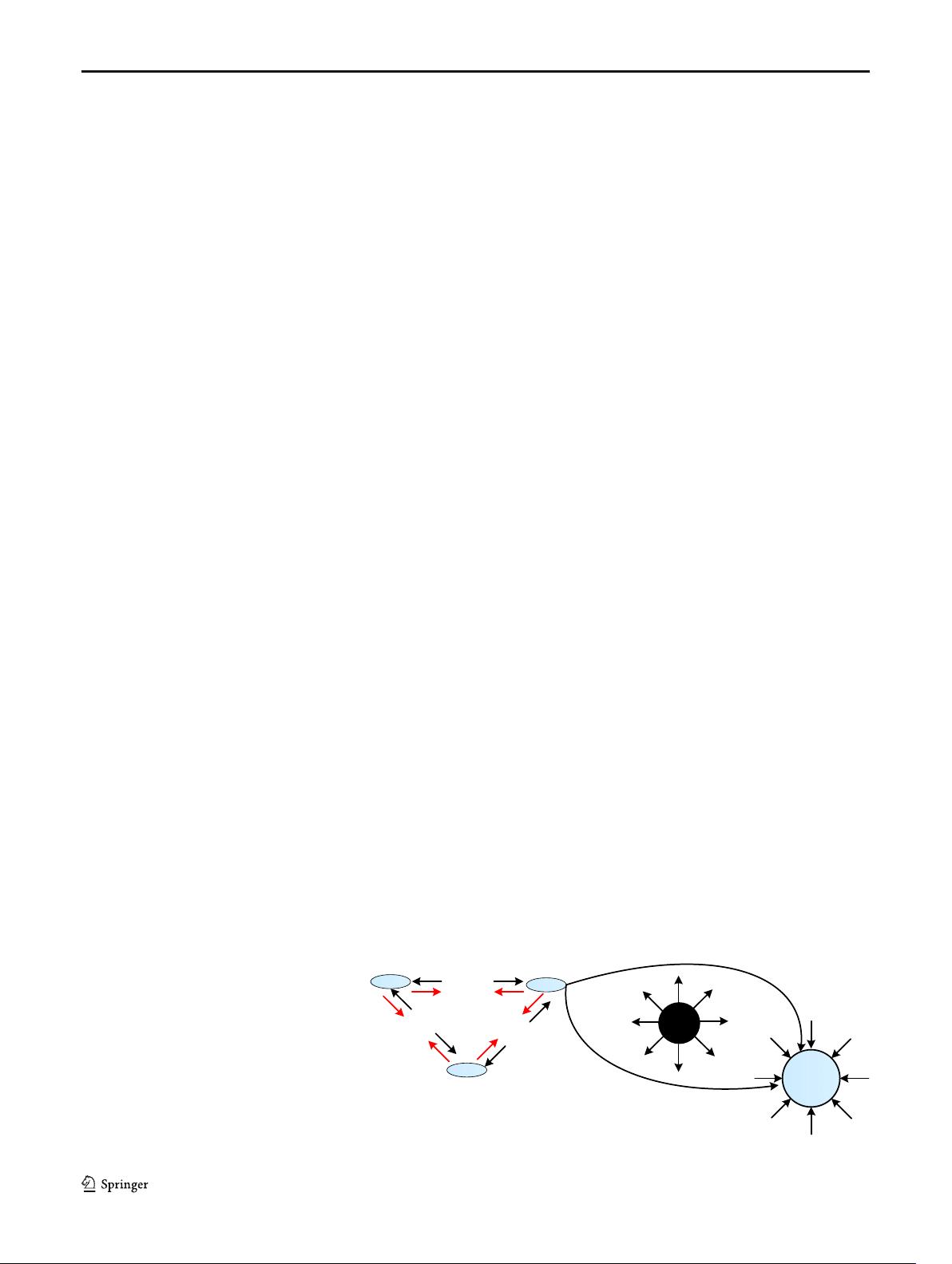
3.3 Formation Control Based on Behavioral Structure

Behavior-based formation control was first introduced by

Balch and Arkin in formation control [51]. This method uses

a weighted hybrid of different mission objectives in order to

generate vehicle control inputs. Generally, control targets in-

clude maintaining desired formation, moving towards the tar-

get, avoiding obstacle collisions, and avoiding inter-group

collisions. Each of the aforementioned items is prioritized

with different gains and the obtained average is given to each

vehicle as a control input. Meeting several control objectives

simultaneously is one of the benefits of this approach. It is,

however, hard to describe the dynamic of the group and guar-

antee the stability of the whole system, because the kinematic

and dynamic features of the vehicle are not taken into consid-

eration. The behavioral structure method is commonly applied

in combination with the artificial potential field method. In

[52], the formation control of a swarm of robots is considered

on the basis of the behavioral method for the generation of

formation and obstacles avoidance. To create an initial forma-

tion, the classification-based target searching algorithm is

used so that any arbitrary shape can be generated. Moreover,

the behavior-based approach is employed for moving in an

unknown obstacle-strewn environment. Based on the non-

linear dynamic systems theory, the distributed formation con-

trol and obstacle avoidance are presented in [53]. The desired

trajectories are gained based on the behavioral variables’ state

space. A combination of behavior-based formation approach

and artificial potential field is one of the most common

methods of formation control, which is also used for control-

ling a group of AUVs with simplified second-order dynamic

equation. The potential function for each vehicle is defined in

terms of goals, obstacles and formation structures and the

control law is designed based on Lyapunov’sdirectmethod.

This will ensure that the AUVs will effectively follow the goal

and avoid obstacles [54]. The combination of virtual and be-

havioral structures is the focal point of other studies conducted

on combining different methods of formation control. This

approach is used for the formation control of a group of mo-

bile robots. Each robot is modeled by an electric charge. Upon

defining the attraction forces, the robots would move towards

Fig. 4 The virtual structure including three vehicles

J Intell Robot Syst (2021) 101: 

Page 5 of 26 67

a circle. When the repulsive force is defined between the iden-

tical charges, the robots find their relative position in the for-

mation and the robots’ regular polygon is realized. The behav-

ioral structure was defined for obstacle avoidance on the basis

of the rotational potential function [44].

3.4 Formation Control Based on Artificial Potential

Function

The artificial potential field method was first introduced by

Khatib for the purpose of controlling the mechanical manipu-

lator and mobile robots [55]. In this approach, interaction con-

trol forces are used between AUVs in order to generate the

desired formation. The attractive and repulsive potential func-

tions are defined. The attractive potential force helps maintain

the desired distances between the AUVs and prevent an in-

crease in the distance between the members of the group. The

repulsive potential force, however, prevents a decrease in the

distance between the vehicles, the probability of collision with

each other, and the likelihood of obstacle collision. The stan-

dard form of the attractive potential function is a quadratic

function of the inter-vehicle distance which increases squarely

as the inter-vehicle distance increases. The repulsive potential

function is in inverse proportion to the distance from obstacles

as well as to the inter-group member distance and increases as

distance decreases. The potential force is obtained from the

addition of negative gradient of attractive and repulsive func-

tions. Figure 5 displays the direction of interactive forces to-

wards the target and the maintenance of the shape of the for-

mation. A fleet of gliders as mobile sensors is used in [56]in

order to collect the most possible amount of oceanographic

data. The cooperative control strategy is based on the potential

function and the virtual leader. Vehicles are modeled as point

masses. The swarm formation control of robots is experimen-

tally presented in [57] using potential functions along with

limit functions. Formation can also be generated by means

of a desired kinematic model on the basis of the artificial

potential function [58]. In [59], the saturated artificial potential

function is utilized in designing an adaptive decentralized

controller for mobile robots’ formation control. Table 1 com-

pares the different structures of formation control and summa-

rizes the strengths and weaknesses of each one.

3.5 Other Formation Control Strategies

In what follows, other methods employed in formation control

are addressed.

3.5.1 Formation Reference Point Method

In the Formation Reference Point (FRP) method, a certain

point is taken as a formation reference point and each AUV

has the desired distance and direction from this point. The

reference point in Fig. 6 follows a parameterized path with a

desired formation velocity and each AUV follows the FRP

with a predetermined distance [60–62]. In this method, the

group is more resistant to the fault or loss of any of the

AUVs because it is not referred to the leader and maintains

its position relative to the FRP point.

3.5.2 Formation Control Based on Graph Theory

Using the graph theory is of the most common methods in

formation control and its stability analysis. In this approach,

the vehicles communicate i nformation by means of a

predetermined directional communicational grap h. In this

method, the vehicles are defined as ‘node’ and the interaction

betweenthemistermedas‘graph edge’ [63–65]. In [66], the

distributed formation control for autonomous underwater ro-

bots was presented on the basis of the graph theory. The for-

mation aims to reach the desired trajectory of the formation

center, a time-varying formation pattern, and the alignments

of device directions.

3.5.3 Shape Formation

In formation shape, there is no definite shape in the placement

of AUVs in relation to each other. The only factors which are

taken in this approach are placement in the desired region and

collision avoidance [67, 68]. The use of proportional-

derivative-adaptive controller for the formation shape of sev-

eral AUVs was presented in [68] by considering uncertainty in

gravitation and buoyance matrices.

rep

att

Obstacle

Target

att

rep

Fig. 5 Formation based on

artificial potential method

J Intell Robot Syst (2021) 101: 

67 Page6 of 26

剩余25页未读，继续阅读

m0_49306194

粉丝: 0
资源: 6

多自主水下机器人路径规划与编队控制综述

Formation Control of Multi-Agent Systems.7z

Distributed formation control for a cooperative multi-agent system

A survey of multi-agent formation control.pdf

and I want to know more about the political impact of the viking age

Please introduce the following in detail: Review of existing research on analyzing metal-transfer images in GMAW process

how dose our brain work to from memories?

distributed formation control of nonholonomic mobile robots without global p

最新资源