统计学第五章：平均指标与标志变异解析

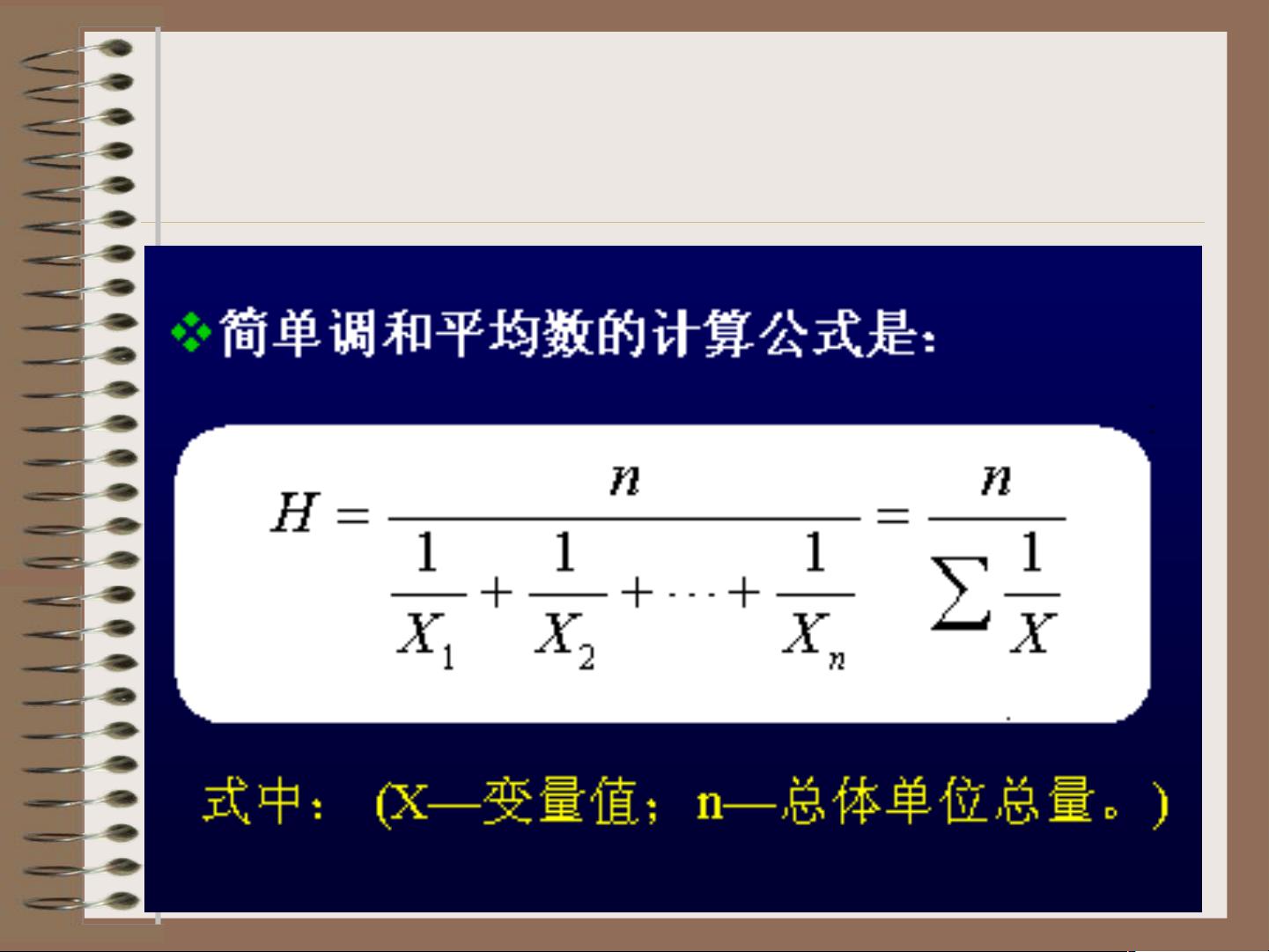
"统计学课程关于第五章平均指标与标志变异指标的讲解" 在统计学中，平均指标是衡量数据集中趋势的重要工具，它能够反映同质总体中某一数量标志值的平均水平。平均指标分为两类：静态平均数和动态平均数。静态平均数描述的是同一时间点上各单元的平均值，而动态平均数则关注不同时间点上的平均值变化。在本章中，主要探讨的是静态平均数。 平均指标的作用主要包括四个方面： 1. 比较不同群体或时间点的平均状态，如比较不同国家的人均收入。 2. 分析同一群体在不同时间的发展变化，如追踪一个地区的平均工资增长。 3. 揭示现象间的关联性，如通过平均消费支出分析收入与消费的关系。 4. 进行预测和推算，基于过去的平均值预测未来的趋势。 平均指标又可以进一步细分为数值平均数和位置平均数。数值平均数包括算术平均数、调和平均数和几何平均数，它们都是基于总体所有数值计算得出的。算术平均数是最常见的，即所有数值相加后除以数值个数。简单算术平均数适用于总体单位已知且无权重的情况，如上述例子中工人的日产量平均数。而在总体被分组或有不同权重的情况下，会采用加权算术平均数，其中每个数值会根据其对应的权重进行调整。 位置平均数，如中位数和众数，不依赖于所有数值，而是基于数据分布的位置。中位数是将数据排序后位于中间的值，众数是出现频率最高的值。这些位置平均数在处理偏斜分布或者异常值较多的数据集时特别有用，因为它们不受极端值的影响。 标志变异指标则是衡量数据分散程度的指标，包括全距、平均差、方差、标准差等，它们提供了关于数据离中趋势和稳定性的重要信息。例如，方差和标准差是衡量数值相对于平均数的离散程度，而全距则反映了数据范围的大小。 本章的学习将帮助我们理解和应用这些统计概念，以便更准确地分析和解释数据。无论是进行经济分析、市场调研还是科学研究，掌握平均指标与标志变异指标都是非常基础且关键的统计技能。