树状数组详解：高效维护前缀和

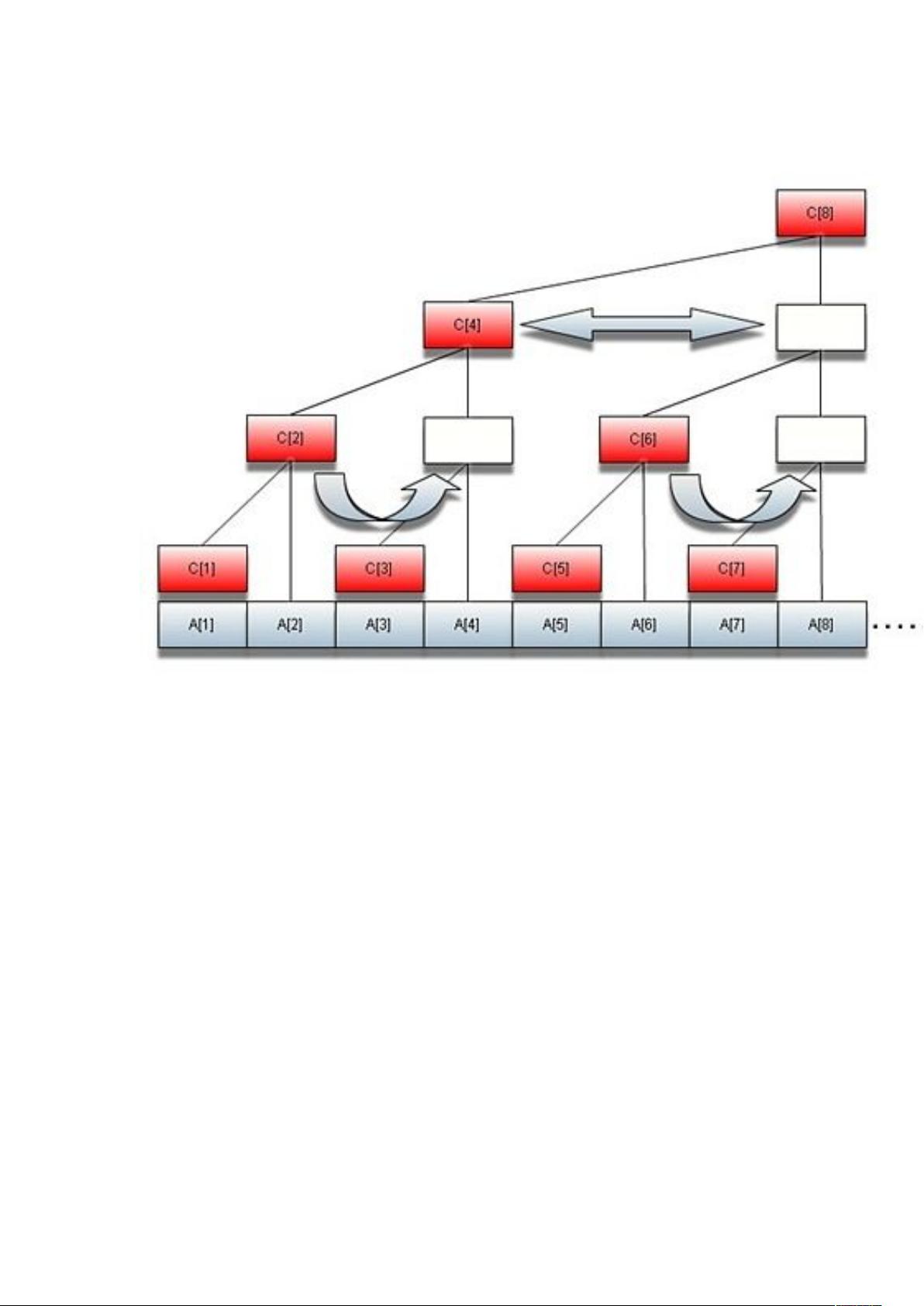
"这篇资源是关于ACM竞赛中常用的树状数组数据结构的讲解，旨在帮助读者理解如何使用树状数组来高效地处理数组的前缀和问题。内容包括理论解释、操作规律以及代码实现，适合对算法和数据结构感兴趣的读者学习。" 树状数组是一种高效的数据结构，主要用来快速计算数组的前缀和并支持动态更新。在ACM（国际大学生程序设计竞赛）等算法竞赛中，树状数组因其高效性能而被广泛应用。 **理论部分** 树状数组，又称为二分索引树或 Fenwick 树，它能够以 O(log n) 的时间复杂度完成两种基本操作：修改数组元素和查询前缀和。这种数据结构的核心思想是将数组元素的和存储在一个压缩的树形结构中，每个节点代表一段连续的数组元素的和。 **构建过程** 以数组 A 为例，树状数组 C 的元素 C[i] 存储的是 A[i - 2^k + 1] 到 A[i] 的和，其中 k 是 i 在二进制表示中末尾 0 的个数。例如，C[8] 表示 A[1] 到 A[8] 的和。由于 k 的最大值不超过 log_2(n)，树的高度也因此不会超过 log_2(n)。 **修改操作** 当我们修改 A[i] 的值时，需要从 C[i] 开始向上遍历到根节点，更新路径上的所有 C[j]，j 是 i 的所有父节点。这个过程只需要 O(log n) 时间。 **查询操作** 查询前缀和 S[i] 可以通过遍历以 i 为根的子树的所有祖先节点的 C[j] 来完成，同样只需要 O(log n) 时间。 **下标规律** - 修改操作：父节点的下标 p = i + 2^k，其中 2^k 是 i 用 2 的幂展开式中的最小幂。 - 查询操作：前一个子树的下标 p = i - (i & (i ^ (i - 1)))，这里的位运算用于找出 i 二进制表示中最右边的 1 所对应的 2 的幂。 **代码实现** 在实际编程中，通常会用到以下函数来实现树状数组的基本操作： 1. 初始化树状数组：通常用一个循环将数组 A 的元素初始值复制到 C 数组中。 2. `update(int i, int val)`：更新数组 A 中的第 i 个元素，增加或减少 val 值，相应地更新树状数组。 3. `getSum(int i)`：返回数组 A 的前 i 个元素的和，即查询树状数组中 C[i] 对应的前缀和。 4. `intLowbit(int t)`：这个辅助函数用于找到 t 二进制表示中最右边的 1 对应的 2 的幂，即 t & (-t)。 在理解和掌握了树状数组的理论和操作后，通过实践编写代码，可以更好地掌握这一高效数据结构，并在解决动态前缀和问题时提高算法效率。