概率论与数理统计习题解答：独立事件、概率密度函数与二元正态分布

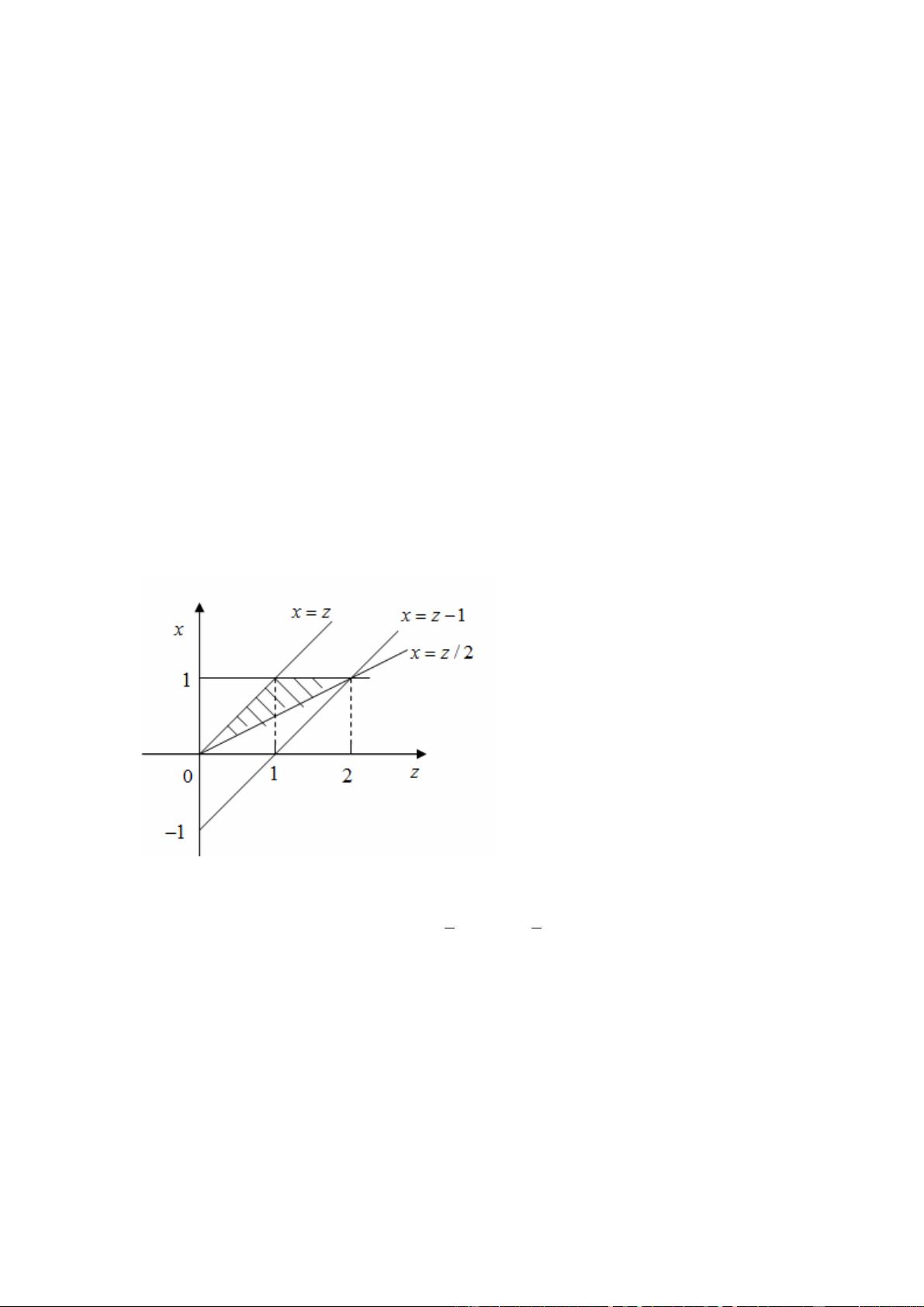
"概率论与数理统计的配套答案，包含独立事件概率计算、参数估计、概率密度函数应用、二元正态分布及样本统计量的分布" 在这份资料中，我们可以看到多个概率论与数理统计中的核心知识点： 1. **独立事件的概率计算**：题目中提到事件A, B, C相互独立，并给出了各自及它们的并集的概率。根据独立事件的性质，如果事件A, B, C相互独立，那么有PA = 0.5, P(B) = 0.6, P(C|A) = 0.4。要求计算P(B)和P(A∪B∪C)。对于P(B)，由于事件B与A无关，所以P(B) = 0.6；对于P(A∪B∪C)，可以利用概率的加法公式和减法规则来求解，最终得到P(A∪B∪C) = 1 - P(非A且非B且非C)。 2. **参数估计**：这里涉及到两个问题，一是最大观测值小于1.8且最小观测值大于0.4的概率，二是未知参数θ的矩估计。第一部分可以通过二项分布计算，第二部分利用矩估计方法，即用样本均值作为总体均值的估计。 3. **概率密度函数及其应用**：给出了一种随机变量X的概率密度函数，它是指数分布，形式为f(x) = (1/5)e^(-x/5)，x > 0。求解的是在10分钟内至少有1位顾客进入的概率。这需要用到连续随机变量的生存函数或累积分布函数，以及指数分布的期望值来计算。 4. **二元正态分布**：男性成年人的身高X和体重Y服从二维正态分布，给出了它们的均值和方差，以及相关系数ρ。当从该地区随机选取n名男子时，他们的身高X的平均值和方差可以通过样本统计量来估计，这里涉及到了样本均值的抽样分布，即n个独立同分布的正态变量的均值也服从正态分布，其均值等于总体均值，方差等于总体方差除以n。 以上知识点涵盖了概率论与数理统计的基础概念，包括独立事件、概率密度函数、参数估计和多元正态分布。这些内容是学习概率论与数理统计的基础，对于理解和应用统计学方法至关重要。