In the Bayesian approach, we regard the function f as the
realization of a random field with a known prior probability
distribution. We are interested in maximizing the a posteriori
probability of f given the data D
f
, namely P½f jD
f
, which can be
written as
P½f jD
f
p P½D
f
jf P½f ; ð5Þ
where P½D
f
jf is the conditional probability of the data D
f
given the
function f and P½f is a priori probability of random field f, which is
often written as P½f p expð
λ Φ½f Þ, where Φ½ f is a smoothness
functional. The probability P½D
f
jf is essentially a model of the
noise, and if the noise is additive, as in Eq. (3) and i.i.d. with
probability distribution Pðe
i
Þ, P½D
f
jf can be written as
P½D
f
jf ¼ ∏
l
i ¼ 1
Pðe
i
Þ: ð6Þ
Substituting P½f and Eq. (6) in (5), maximizing the posterior
probability of f given the data D
f
is equal to minimizing the
following functional
H½f ¼ ∑
l
i ¼ 1
log ½Pðy
i
f ðx
i
ÞÞ e
λ
Φ
½f
¼ ∑
l
i ¼ 1
log Pðy
i
f ðx
i
ÞÞþλ Φ½f : ð7Þ
This functional is of the same form as Eq. (4) [29]. By Eqs.
(4) and (7), the optimal loss function in maximum a posteriori is
cðeÞ¼cðx; y; f ðxÞÞ ¼ log pðy f ðxÞÞ : ð8Þ
We assume that the noise in Eq. (3) is Laplace, with the
probability density function Pðe
i
Þ¼
1
2
e
je
i
j
. By Eq. (8), the loss
function should be cðe
i
Þ¼je
i
j (i ¼ 1; …; l).
If the noise in Eq. (3) is Gaussian, with zero mean and standard
deviation
σ
, then by Eq. (8) the loss function corresponding to
Gaussian noise is cðe
i
Þ¼
1
2
σ
2
e
2
i
(i ¼ 1; …; l).
And if the noise in Eq. (3) is Beta, with mean
μA ð0; 1Þ and
standard deviation
σ
, then by Eq. (8), the loss function correspond-
ing to Beta noise is cðe
i
Þ¼ð1mÞlog ðe
i
Þþð1nÞ log ð1 e
i
Þ,
0o e
i
o 1(i ¼ 1; …; l), m4 1; n4 1.
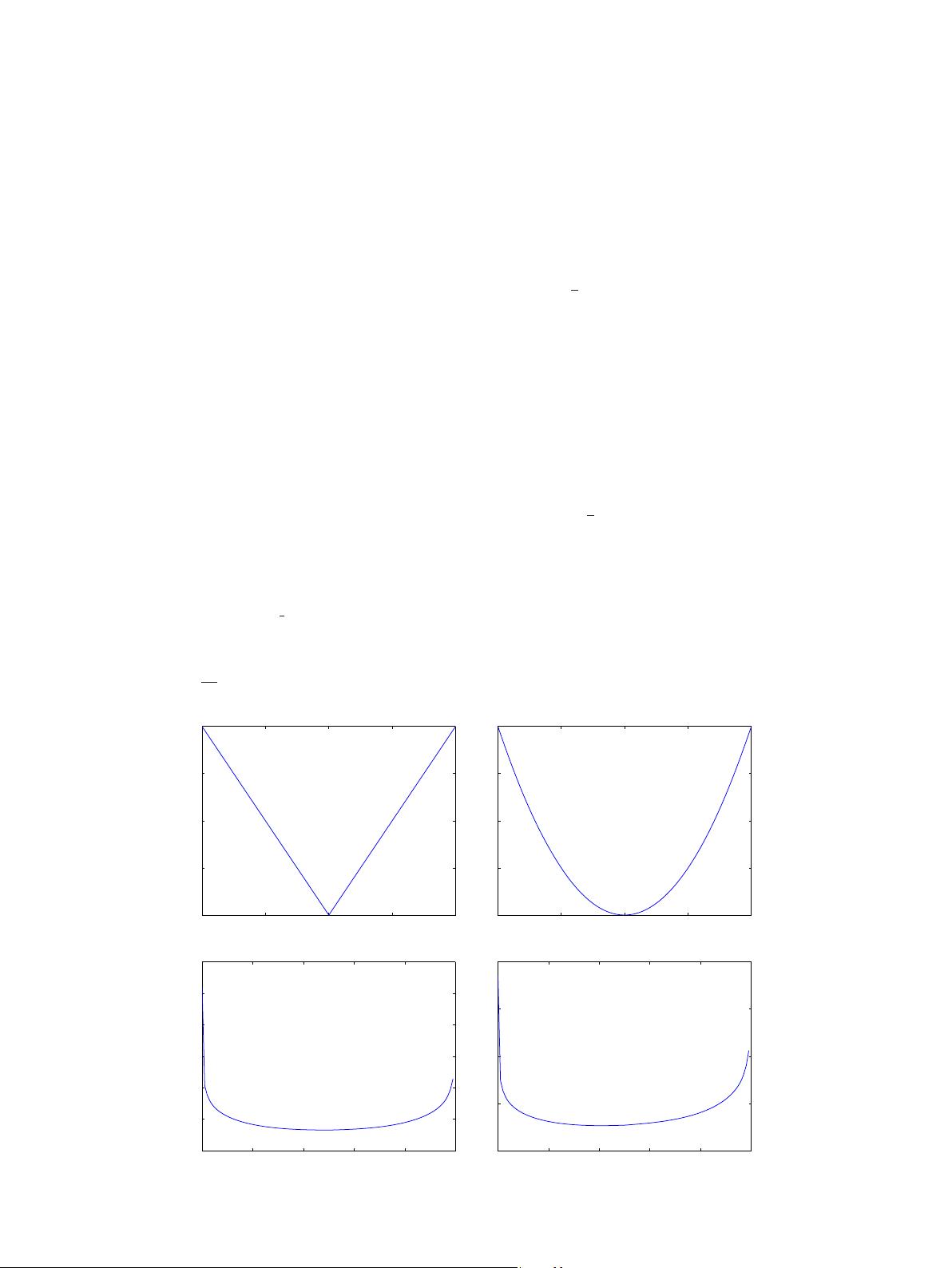
The Laplacian loss function, the Gaussian loss function and the
Beta loss function of parameters are shown in Fig. 2.
Give samples D
l
, we construct a nonlinear regression function
f ðxÞ¼
ω
T
ΦðxÞþb. The uniform model of kernel ridge regression
technique for the general noise model (N-KRR) can be formally
defined as
min g
P
N KRR
¼
1
2
ω
T
ωþ C ∑
l
i ¼ 1
cðe
i
Þ
()
P
N KRR
: s:t: y
i
ω
T
Φðx
i
Þb ¼ e
i
ði ¼ 1; …; lÞ; ð9Þ
cðe
i
ÞZ 0ði ¼ 1; 2; …; lÞ are general convex loss functions in the
sample point ðx
i
; y
i
ÞA D
l
. C 4 0 is a penalty parameter.
We construct a Lagrangian function from the primal objective
function and the corresponding constraints by introducing a dual
set of variables. Standard Lagrangian techniques are used to derive
the dual problem.
Theorem 1. The dual problem of the primal problem (9) of N-KRR is
max g
D
N KRR
¼
1
2
∑
l
i ¼ 1
∑
l
j ¼ 1
ðα
i
α
j
Kðx
i
; x
j
ÞÞ
(
þ ∑
l
i ¼ 1
ðα
i
y
i
ÞþC ∑
l
i ¼ 1
ðTðe
i
ðα
i
ÞÞ
)
ð10Þ
D
N KRR
: s:t: ∑
l
i ¼ 1
α
i
¼ 0;
where Tðe
i
ðα
i
ÞÞ ¼ cðe
i
ðα
i
ÞÞe
i
ðα
i
Þ∂ðcðe
i
ðα
i
ÞÞÞ=∂ðe
i
ðα
i
ÞÞ, e
i
is a func-
tion of variable
α
i
(i ¼ 1; …; l), C 4 0 is constant.
−2 −1 0 1 2
0
0.5
1
1.5
2
Laplacian Loss function
−2 −1 0 1 2
0
0.5
1
1.5
2
Gaussian Loss function
0 0.2 0.4 0.6 0.8 1
0
10
20
30
40
50
60
Beta Loss function,m=n=5.5
0 0.2 0.4 0.6 0.8 1
0
5
10
15
20
Beta Loss function,m=2.6084,n=3.0889
Fig. 2. Laplacian loss function, Gaussian loss function and Beta loss function of parameters.
S. Zhang et al. / Neurocomputing 149 (2015) 836–846838









