"数学建模学习方法-主成分和因子分析：降维处理高维数据"

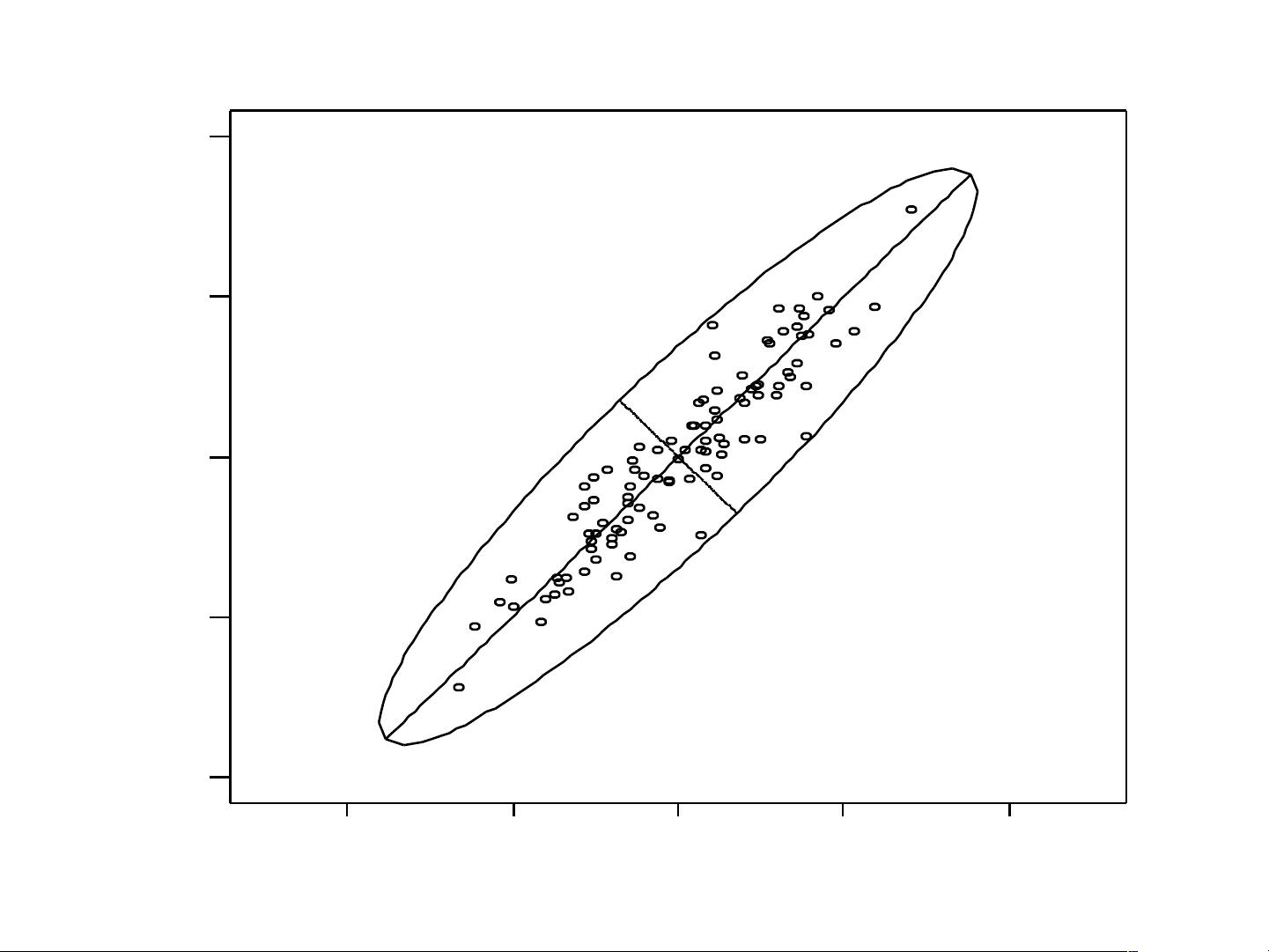
• 个维度进行降维，以便于更简洁地描述学生的成绩情况？• 能否找到少数几个“代表”来代替原有的六个变量，但又不失真实性和描述力？• 降低维数后，这几个“代表”是否可以更好地反映学生的整体情况，以及学科之间的关联情况？ 主成分分析和因子分析就是用来解决这类问题的方法。它们可以通过对原始数据进行数学变换，得到少数几个新的综合变量，这些新变量被称为主成分或者因子。主成分和因子可以比原始变量更好地描述数据的特点，同时还能保留原始数据中的大部分信息，从而实现数据降维和信息概括的目的。 主成分分析是一种无监督学习方法，它通过对协方差矩阵的特征值和特征向量进行分解，得到一组新的由原始变量线性组合而成的主成分。这些主成分按照其所包含的原始变量的信息量大小，依次排列，前几个主成分通常可以解释原始数据中绝大部分的方差，从而实现维数的降低。 因子分析与主成分分析有着相似的思想，它也是通过对协方差矩阵或相关矩阵的因子载荷矩阵进行分解，得到一组新的综合变量，这些综合变量被称为因子。不同的是，因子分析更注重的是寻找潜在的、不能直接观测到的影响原始变量的因子，而不是简单地对原始变量进行线性组合。因子分析通常可以帮助我们揭示数据背后的潜在结构和变量之间的关联性。 在实际应用中，主成分分析和因子分析可以帮助我们更好地理解数据的性质和结构，发现潜在的变量或隐藏的信息，简化复杂的数据集，提取重要的特征，从而有利于进一步的数据分析和挖掘。它们在金融、经济、市场调查、心理学、社会学等领域都有着广泛的应用。 总之，主成分分析和因子分析是一种重要的数据降维和信息概括的方法，它们可以帮助我们更好地理解和描述数据，发现数据背后的规律和结构，从而为后续的数据分析和决策提供重要的参考。在实际应用中，我们可以根据具体的问题和数据特点，选择适合的方法进行分析，并结合领域知识和实际情况，充分发挥主成分分析和因子分析的作用。