正交变换与奇异值分解(SVD)解析

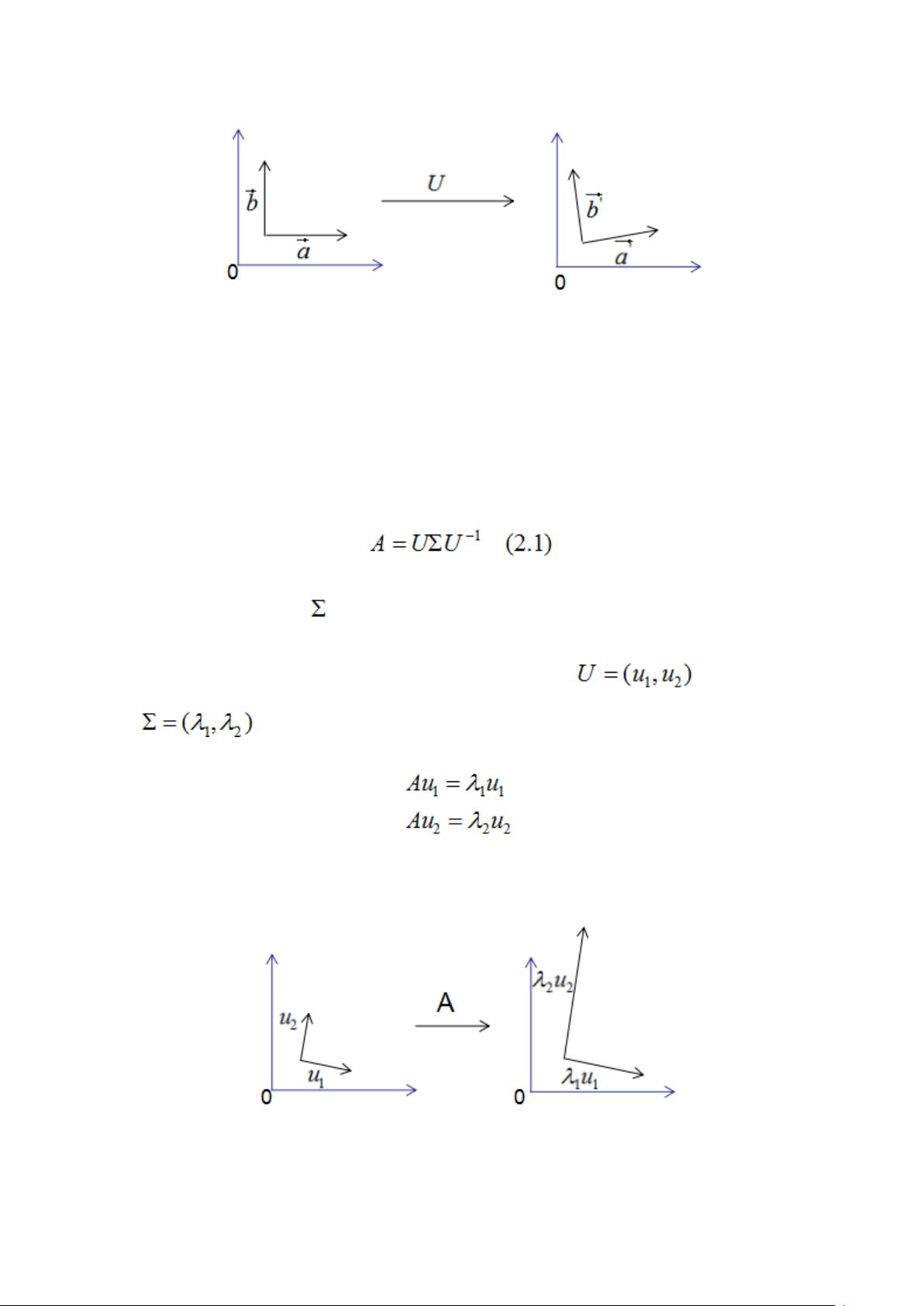
"奇异值分解总结" 奇异值分解（Singular Value Decomposition，SVD）是一种重要的线性代数技术，广泛应用于数据压缩、图像处理、机器学习等多个领域。本文将从正交变换、特征值分解和SVD的推导三个方面进行深入探讨。 1. 正交变换 正交变换是指保持向量间夹角和长度不变的线性变换，通常由正交矩阵实现。正交矩阵的每一列（或行）都是单位向量，且它们相互之间垂直。正交变换对于理解和解析矩阵作用于向量的方式至关重要，因为它揭示了矩阵如何保留向量的几何特性。 2. 特征值分解 特征值分解是针对对称矩阵的一种特殊分解，其中矩阵A可以表示为其特征向量所组成的矩阵U与一个对角矩阵Λ的乘积，对角线上元素为特征值。对称矩阵的特征向量是正交的，而且矩阵A对特征向量仅进行拉伸或缩短，不改变方向。这使得特征值分解在处理对称问题时非常有用，例如在主成分分析（PCA）中。 3. SVD分解推导 奇异值分解是针对任意实数矩阵A的一种分解，它不仅适用于方阵，也适用于非方阵。假设A为M×N矩阵，其秩为K（Rank(A)=k），则存在正交矩阵U和V以及一个对角矩阵Σ，使得A可以表示为A=UDV^T。其中，D是对角矩阵，其对角线上的元素称为奇异值，非零奇异值的个数等于矩阵的秩K。奇异值分解的推导基于正交变换的思想，即使矩阵A作用的向量空间通过正交基进行变换后，仍然保持基的正交性。 在实际应用中，SVD特别适用于处理稀疏矩阵或非方阵，例如在推荐系统中，它可以用来解决用户和物品矩阵的稀疏性问题。此外，SVD在机器学习中用于降维和特征提取，以及在图像处理中的图像压缩等领域都有重要应用。 总结，奇异值分解作为线性代数的基本工具，不仅提供了对矩阵操作的深刻理解，还在实际问题中展现了强大的功能。通过正交变换和特征值分解的基础，我们可以更好地理解和运用SVD，从而解决复杂的数据问题。