自动控制理论：拉普拉斯变换在控制系统中的应用

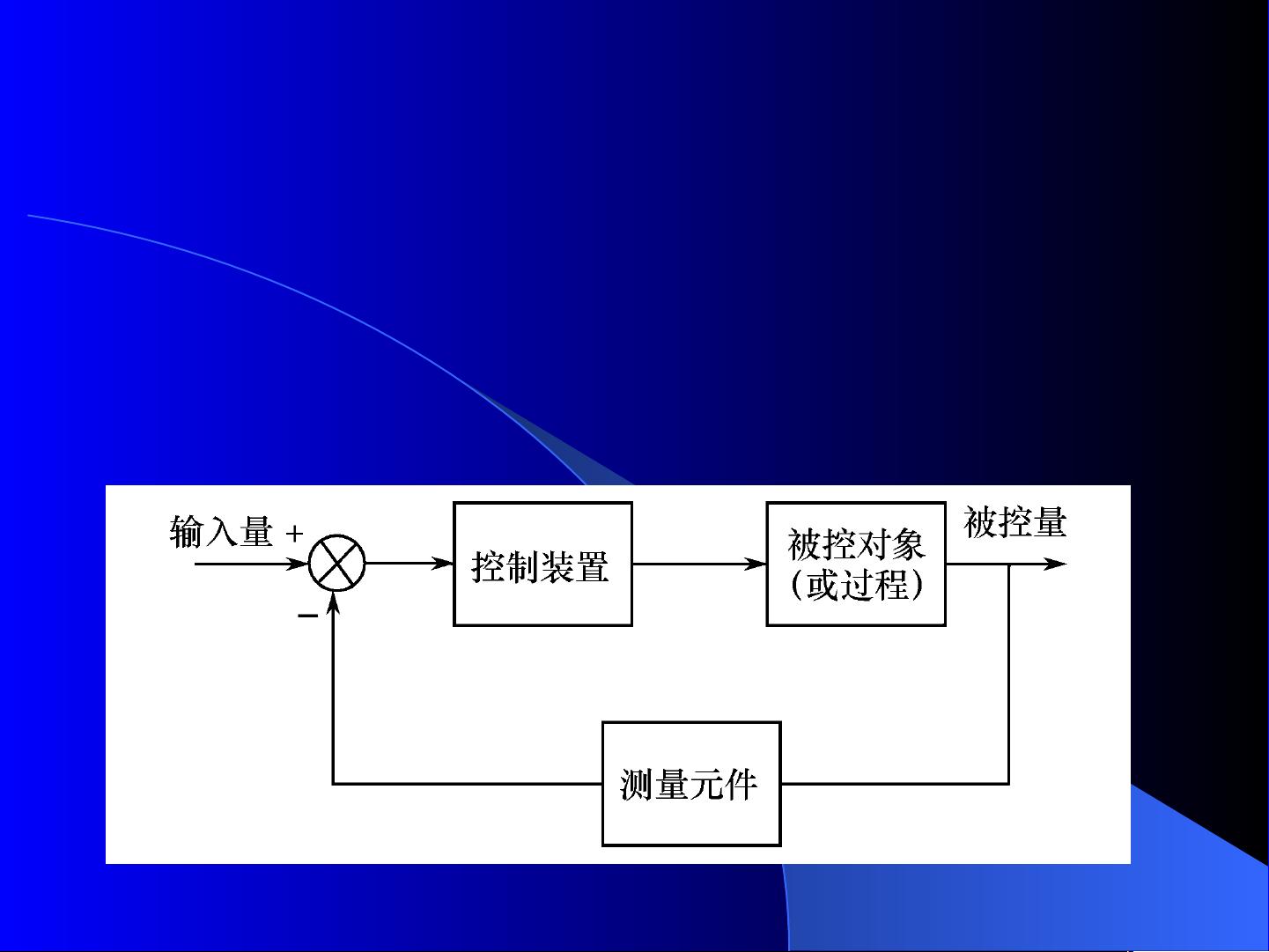
"自动控制理论中的拉普拉斯变换在控制系统分析和设计中起着至关重要的作用。拉普拉斯变换是工程数学中一种重要的工具，它将时间域内的微分方程转化为复频域内的代数方程，简化了对动态系统特性的分析。" 在自动控制理论中，拉普拉斯变换是理解和分析控制系统行为的关键技术之一。拉普拉斯变换能够将连续时间信号转换成其在复频域的表示，这对于解决线性常微分方程非常有效。在控制系统中，这通常涉及到将一个系统的动态模型从时间域转换到复频域，使得我们可以更容易地研究系统的稳定性和响应特性。 自动控制系统分为两种主要类型：开环控制和闭环控制。开环控制系统不包含反馈机制，其控制决策仅基于设定值，而不考虑实际输出。因此，这类系统对扰动和参数变化的鲁棒性较差，控制精度有限。例如，数控机床的进给系统可能采用开环控制。 相比之下，闭环控制（或反馈控制）系统包含了反馈机制，能够根据系统的实际输出调整控制信号，以减少或消除偏差。闭环控制系统通过检测被控量并将其与设定值进行比较，然后根据偏差进行控制，从而提高了系统的稳定性和控制精度。然而，闭环控制系统的设计和实现相对复杂，需要考虑更多的动态性能指标，如超调、上升时间和稳态误差等。 拉普拉斯变换在闭环控制系统分析中尤为有用，因为它可以用来求解描述系统动态行为的微分方程。通过将系统传递函数定义为输入和输出的拉普拉斯变换之比，可以评估系统的频率响应，进而确定系统的稳定性和动态性能。传递函数揭示了系统对不同频率输入信号的反应，帮助工程师选择合适的控制器参数以优化性能。 自动控制课程的主要任务包括理解控制系统的原理，掌握各种控制策略，如PID控制，学习如何使用MATLAB等工具进行系统建模、仿真和分析。通过实际控制系统案例的学习，学生可以深入理解控制理论的应用，并掌握如何设计和改进控制系统以满足性能需求。 自控理论中的拉普拉斯变换是分析和设计控制系统的基础，它提供了在复频域内处理动态问题的方法，使得工程师能够更有效地评估系统的稳定性和性能，进而实现对复杂系统的精确控制。在实际工程中，结合拉普拉斯变换和其他控制理论，可以构建出高效、稳定的自动化解决方案。