机器人领域刚体空间变换解析

"第二章 刚体空间变换1 - 追风少年 - 2016/12/29" 在定位导航和机器人技术中，理解和掌握刚体空间变换至关重要，因为它们涉及到物体在三维空间中的精确位置和姿态描述。刚体变换是描述刚体在空间中运动的基础，它包括平移和旋转，常用于机器人路径规划、视觉定位以及传感器数据融合等领域。 1. 笛卡尔坐标与右手法则 笛卡尔坐标系统是三维空间中最常见的坐标表示方式，通过X、Y、Z三个相互垂直的轴定义点的位置。右手法则则是确定轴之间正交关系的标准方法，用于统一坐标系的建立。在右手坐标系中，拇指代表X轴，食指代表Y轴，中指代表Z轴，确保了旋转方向的一致性，即逆时针旋转为正。 2. 坐标系 - 载体坐标系（Body Coordinate）：通常以移动对象的前进方向为X轴，右侧为Y轴，下方为Z轴。这适用于描述物体自身的运动和测量。 - 世界坐标系（Earth Coordinate）：如ENU坐标系（East, North, Up），常用于地理定位，其中X轴指向正东，Y轴指向正北，Z轴指向上方。世界坐标系提供了全局参考，用于比较和集成来自不同来源的数据。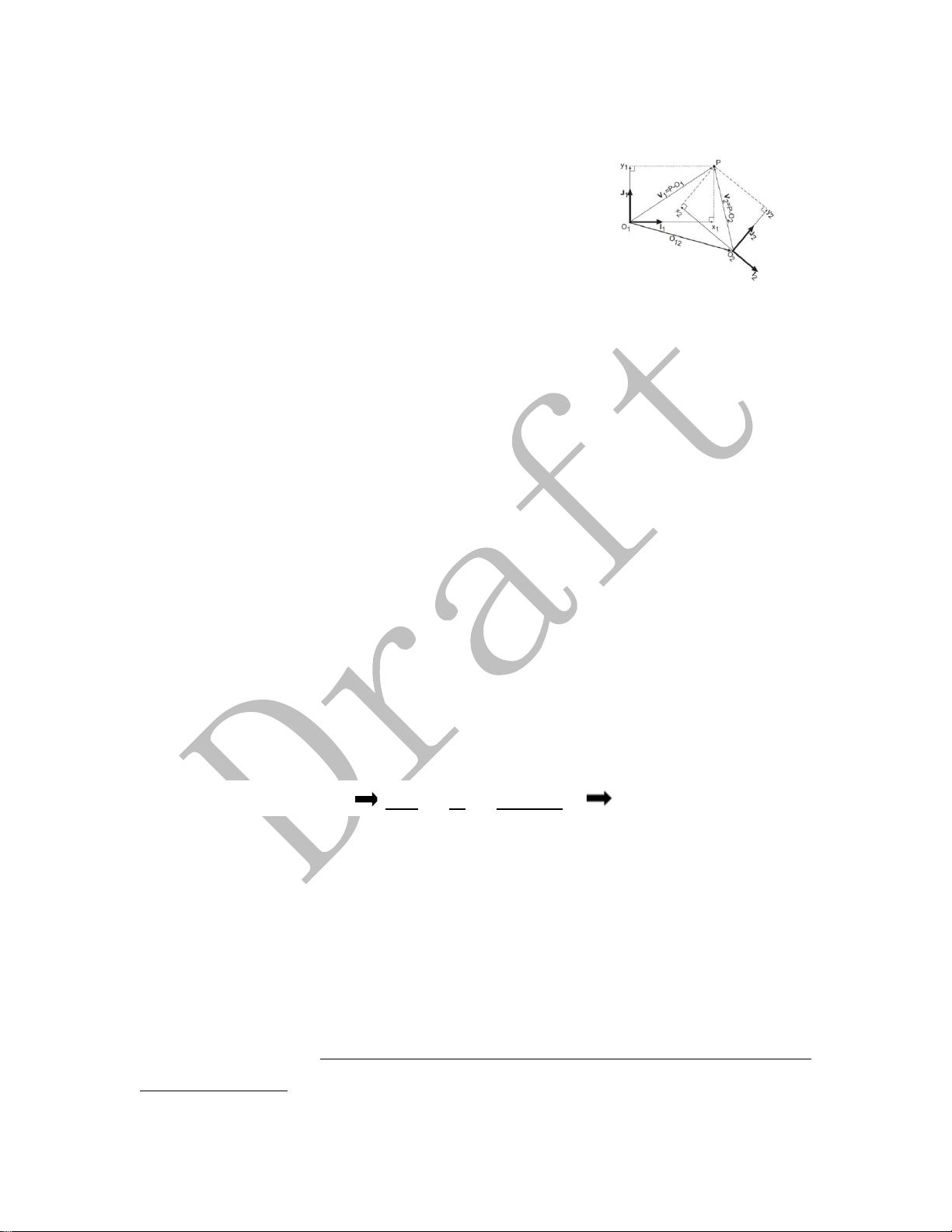 3. 空间变换 空间变换是将物体在载体坐标系中的坐标转换为世界坐标系的过程，以实现不同坐标系间的兼容。这通常涉及平移（Translation）和旋转（Rotation）两种操作。例如，刚体的旋转可以通过欧拉角、四元数或旋转矩阵来描述，而平移则通过一个向量表示。变换通常由一个变换矩阵表示，它可以组合旋转和平移，形成一个从载体坐标系到世界坐标系的映射。 3.1 旋转 - 欧拉角：通过三个旋转角度（如 yaw-pitch-roll 或 roll-pitch-yaw）描述物体的旋转，每个角度对应一个轴的旋转。 - 四元数：一种更稳定且避免万向锁问题的旋转表示，由实部和三个虚部构成，可表示任意角度的旋转。 - 旋转矩阵：3x3的矩阵，每行和每列都是单位向量，表示坐标轴的旋转。 3.2 平移 平移是一个3D向量，表示物体在三个坐标轴上的位移。 在实际应用中，使用开源库进行开发时，必须注意库函数中使用的坐标系和基准，以防止因坐标系不匹配导致的计算错误。例如，有些库可能使用左手坐标系，或者旋转方向与标准相反，因此在调用API前需要仔细阅读文档并进行必要的转换。 总结，刚体空间变换是定位导航和机器人技术中的核心概念，理解并正确应用这些变换对于确保系统准确性和可靠性至关重要。无论是进行路径规划、传感器数据融合，还是进行三维可视化，都需要深入理解和熟练掌握这些基础知识。