红黑树详解：HashMap的转换机制与关键规则

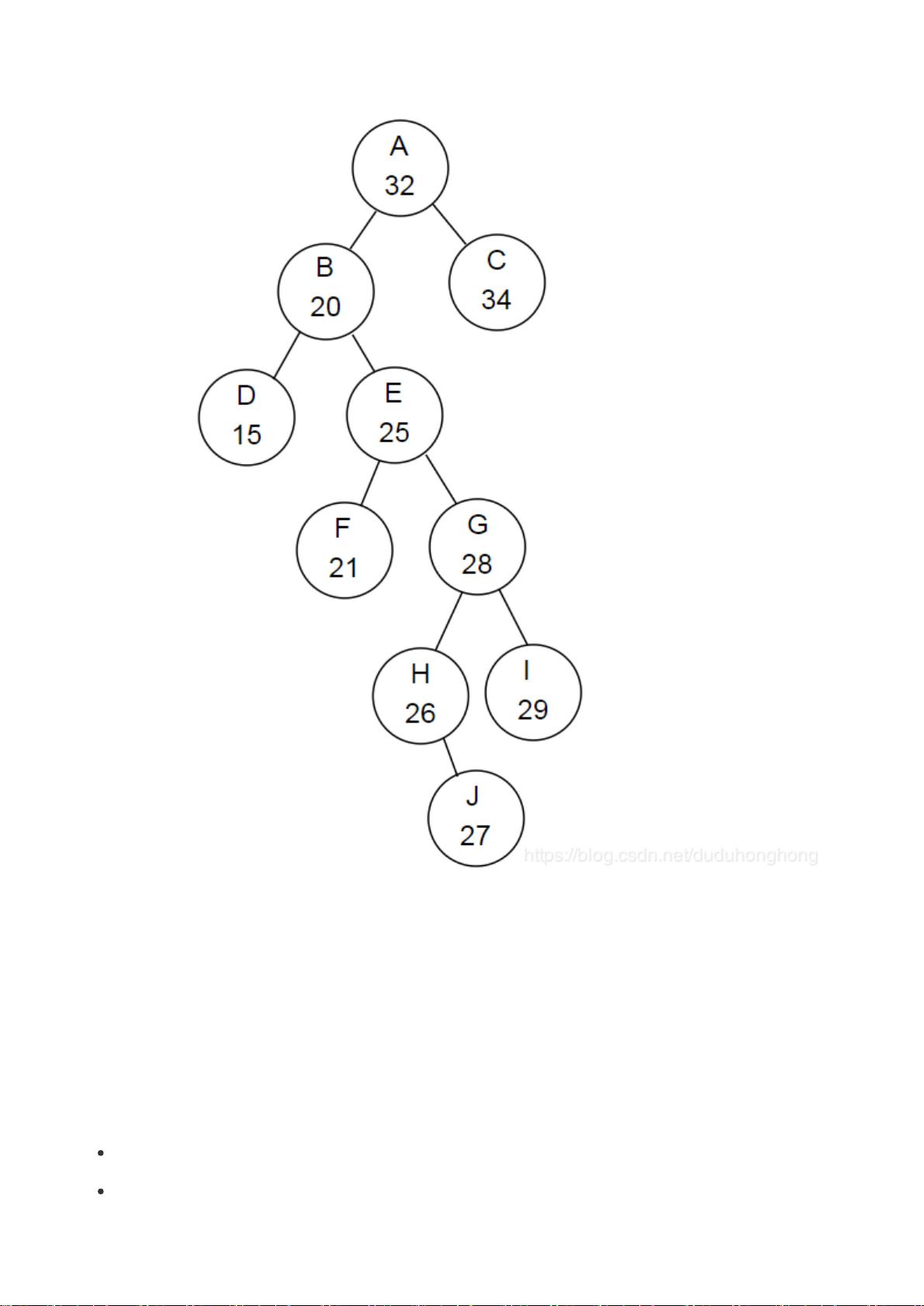
红黑树是一种自平衡的二叉查找树，它在Java编程和其他数据结构中扮演着重要角色，尤其是在处理大量数据和需要高效查询、插入和删除操作的数据结构如HashMap中。HashMap使用数组和链表作为基础存储结构，当链表长度超过特定阈值（通常是8），链表会转换为红黑树，以提高查找、插入和删除的性能。 红黑树的核心概念起源于二叉查找树，其中每个节点的关键字大小决定了其在树中的位置。在插入新节点时，遵循以下规则以保持树的平衡： 1. 颜色属性：每个节点要么是红色，要么是黑色。 2. 根节点颜色：根节点始终保持黑色。 3. 子节点颜色：若节点为红色，则其子节点必须为黑色，但反之不一定是这样。 4. 黑色高度一致性：从根节点到任意叶子节点（或空节点）的所有路径上，黑色节点的数量相同。 这些规则确保了红黑树的性能特性：无论从哪个节点到其远端叶子节点的路径，最长和最短路径的差不超过一个黑色节点。这意味着即使在最坏情况下，搜索时间复杂度仍为O(log n)，而非二叉查找树的最坏情况O(n)。 插入节点的过程是关键步骤，遵循插入后可能需要进行颜色调整（变色）和旋转（包括左旋和右旋）来维护规则。插入一个红色节点不会立即违反规则，但如果插入导致违反规则，就需要通过调整颜色和旋转来恢复平衡。例如，如果插入导致某个路径上有过多的黑色节点，可能会通过变色（将某些父节点由黑色变为红色）和旋转来平衡。 红黑树以其高效性和易于实现的特点，在Java编程和数据结构设计中广泛应用，对于理解底层数据结构的运作原理和优化算法性能具有重要意义。掌握红黑树的工作原理和操作方法，是成为高级程序员和算法工程师的重要一步。