没有合适的资源?快使用搜索试试~ 我知道了~
首页卡尔曼滤波那点事---Android 9DOF算法
资源详情
资源评论
资源推荐

卡尔曼滤波那点事---Android 9DOF 算法
卡尔曼滤波那点事---Android 9DOF 算法.......................................................................................1
1. 前言.................................................................................................................................................1
2. Kalman Filter theory.......................................................................................................................1
2.1. General.................................................................................................................................1
2.2. 非线性的卡尔曼滤波方程..................................................................................................5
2.3. 9DOF 算法一:严格的非线性 KalmanFilter....................................................................7
2.4. Indirect Kalman Filter for 3D Attitude Estimation............................................................10
3. Scilab 代码....................................................................................................................................12
3.1. 卡尔曼滤波修正 gyro bias 和计算方向余弦...................................................................12
3.2. Kalman 滤波计算线性加速度..........................................................................................24
1. 前言
卡尔曼滤波其实是用测量量来对系统状态参数进行修正的一种方式。对于刚接触的人而言
最需要的是一个实际使用的实例分析。本文以 android 代码中的 9DOF 算法为例,从卡尔曼
的基本原理,到非线性卡尔曼滤波方程,最后到 android 实际使用的 Indirect Kalman filter。
让大家能够看明白卡尔曼滤波是如何在实际工程中使用的。
整文分两部分。第一部分为理论。重点把结果罗列了一下。本文不是教材,所以推导过程
都省略了。第二部分是代码。代码有些奇怪,用 scilab 写的,而不是 matlab。scilab 是开源
的类 matlab 的工具,对业余爱好者足够。语法也基本类似。
文中的公式都标明了出处。我尽可能避免公式写错。如果有怀疑,可以和后面的代码对照。
最后,如果有问题需要探讨,可以联系:bigstone1998@sina.com。不过回复可能很不及时。
2. Kalman Filter theory
2.1.General
Kalman filter 首先是离散线性系统的 kalman filter。下面就有。
接下去是连续线性系统的 kalman filter。这个把系统离散化就可以。
下面公式来自 Wiki。大家从教材或网上都可以查到。

物理意义:
特别说明一下 P。P 是 covariance of X。例如,如果 X 是 2 维矢量,那么 P 就是一个 2*2 矩
阵。含义是协方差。
启动 Kalman 算法的时候,需要初始值。初始值应该理解为
X
k∨k−1
, P
k∨k−1
。因为它们都是
非修正值。
以 g=1 的星球上的自由落体为例,来说明 Kalman Filter 的物理意义。这个问题可以描述为:
我们大致知道在 g=1 的星球上,一个物体在 100 米左右,可能有初速度 1 以内的位置开始
下落。每 1 秒钟我们有机会对这个物体进行一次观测,但是观测的精度也是在 1 米以内。
看看如果用 Kalman Filter 方式来修正我们的对物体运动的预测。
物理规律大家都知道:
¨
y=−g=¿
{
˙
y(t)=
˙
y
t 0
−g(t−t 0)
y
(
t
)
= y
t 0
+
˙
y
t 0
(
t−t 0
)
−
g
2
(t− t 0)
2
把这个方程离散化,假设以 1s 为步长:

{
y
k+1
= y
k
+
˙
y
k
−g/2
˙
y
k +1
=
˙
y
k
−g
以位置和速度为状态参量 X=[y,v]’,可以得到:
X
(
k +1
)
=
[
1 1
0 1
]
X
(
k
)
+
[
0.5
1
]
(
−g
)
从这个状态方程可得到 F,B,u。
然后看测量方程。测量量是位置。位置用状态参量表示为:
Z
(
k
)
=
[
1 0
]
X
(
k
)
+W (k )
从测量方程可以得到 H。至于测量的误差量 W(k),根据假设都是 1 米。所以 R=1。观测值
为:
状态参量可以认为没有噪声,所以 Q=0。
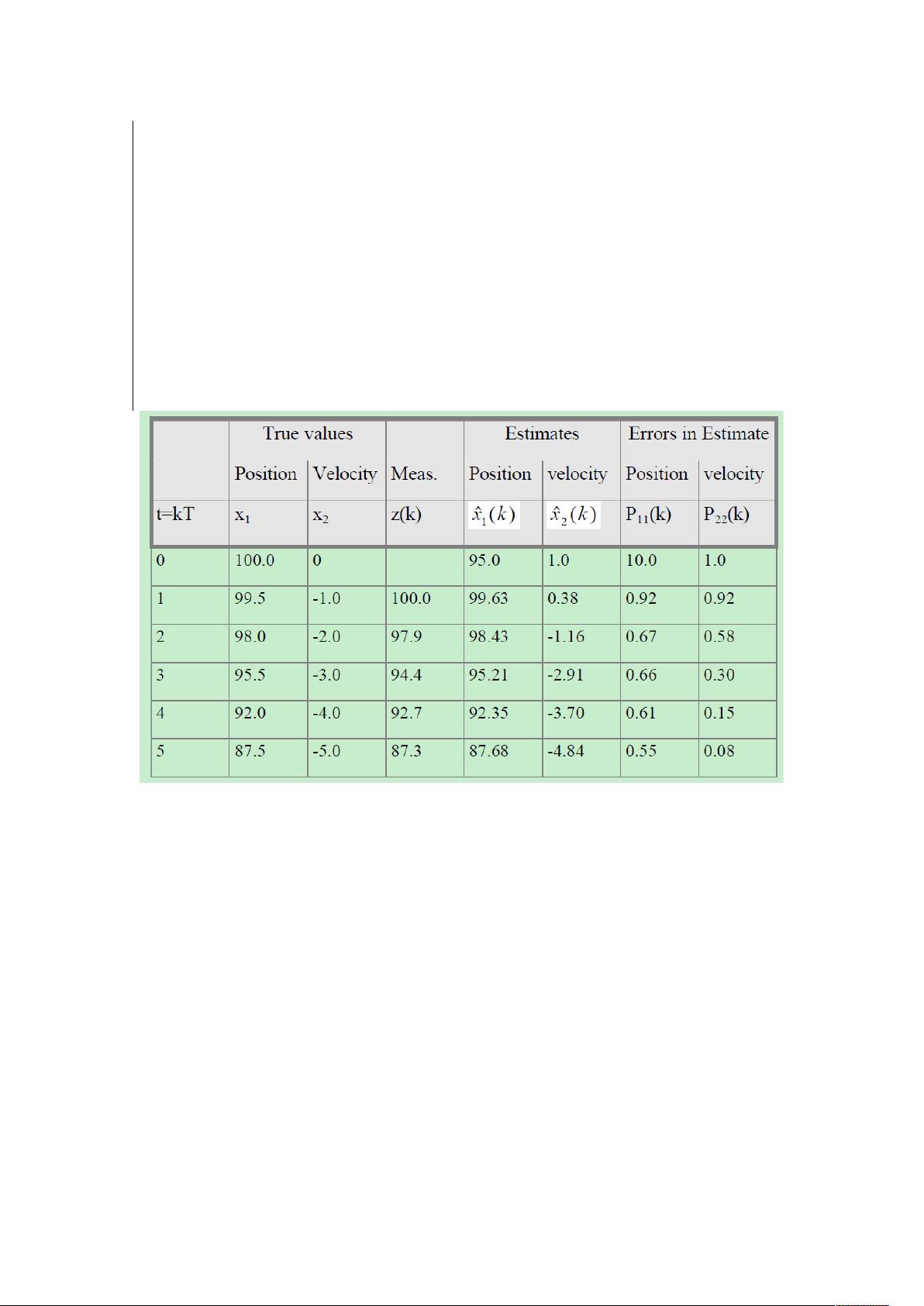
初始位置估计为 95 米,初始速度估计为 1。初始的状态变量的估计偏差位置为 10 米,速度
为 1 米/秒。所以初始值为:[100,97.9,94.4,92.7,87.3]。
X
0∨−1
=
[
95
1
]
; P
0∨−1
=
[
10 0
0 1
]
这样,scilab 的代码为:
F=[1,1;0,1];
B=[0.5,1]';
u=-1;
Q=0
H=[1,0];
Z=[100,100,97.9,94.4,92.7,87.3];
R=[0,1,1,1,1,1];
X21=[];
X22=[];
y=[];
S=[];
K=[];
P21=[];
P22=[];
I=[1,0;0,1];
/////////////////////////////////////
X21(:,1)=[95,1]';// start point
X22(:,1)=[95,0]';
y(1)=0;
S(1)=0;
K(:,1)=[0,0]';
P21(:,:,1)=[10,0;0,1];
P22(:,:,1)=[0,0;0,0];
fori=2:6
// update
y(i)=Z(i)-H*X21(:,i-1);
S(i)=H*P21(:,:,i-1)*H'+R(i);
K(:,i)=P21(:,:,i-1)*H'/S(i);
X22(:,i)=X21(:,i-1)+K(:,i)*y(i);
P22(:,:,i)=(I-K(:,i)*H)*P21(:,:,i-1);
// predict
X21(:,i)=F*X22(:,i)+B*u;
P21(:,:,i)=F*P22(:,:,i)*F'+Q;
end
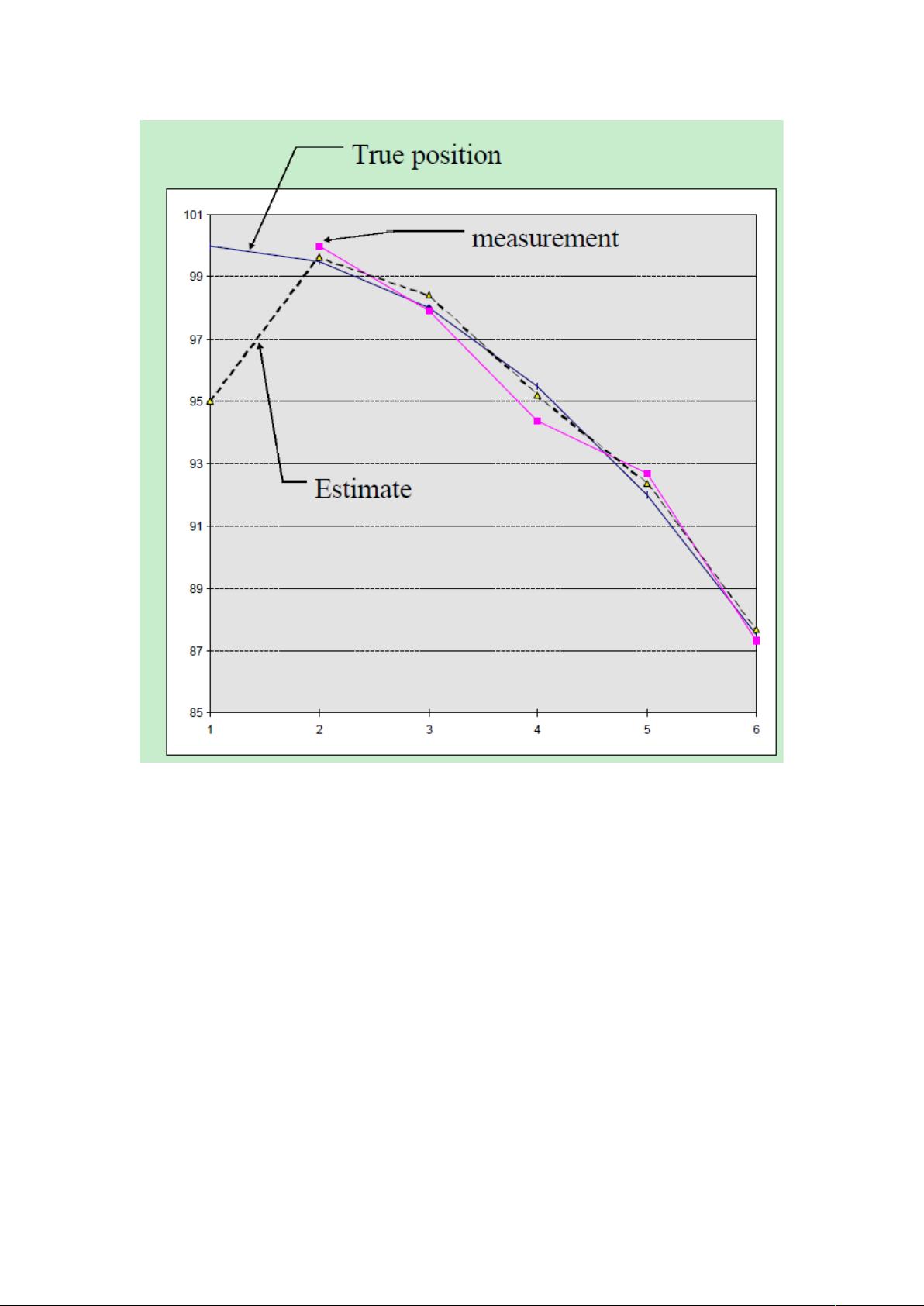
说明:scilab 的运行值和这个稍微有些不同。但基本一样。图中 Estimate 其实是修正后的状
态变量 X22 里面的位置值。
另外,如果设置不同的初始值和初始估计误差,结果会有些不同,但是趋势一样。特别是
初始估计误差。如果设置不合理,比如设置为全 0,那么 Kalman 滤波的结果就会收敛的慢
一些。所以初值的正确估计和合理设置也很重要。注意,P 和 Q 的初始化,必定有一个不
为 0。如果全为 0,就没有必要 Kalman 去修正了。
2.2.非线性的卡尔曼滤波方程
但是不幸的是,我们常遇到的是非线性的连续系统,如我们的 attitude estimation,就是一
个非线性的应用。(参考:《卡尔曼滤波和导航.pdf》P175 $6.2)
通常叫广义卡尔曼滤波(EKF)。推导就省去了,教材都有,结论如下:对于如下非线性系
剩余35页未读,继续阅读
bigstone1998
- 粉丝: 3
- 资源: 13
上传资源 快速赚钱
 我的内容管理
收起
我的内容管理
收起
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

会员权益专享
最新资源
- RTL8188FU-Linux-v5.7.4.2-36687.20200602.tar(20765).gz
- c++校园超市商品信息管理系统课程设计说明书(含源代码) (2).pdf
- 建筑供配电系统相关课件.pptx
- 企业管理规章制度及管理模式.doc
- vb打开摄像头.doc
- 云计算-可信计算中认证协议改进方案.pdf
- [详细完整版]单片机编程4.ppt
- c语言常用算法.pdf
- c++经典程序代码大全.pdf
- 单片机数字时钟资料.doc
- 11项目管理前沿1.0.pptx
- 基于ssm的“魅力”繁峙宣传网站的设计与实现论文.doc
- 智慧交通综合解决方案.pptx
- 建筑防潮设计-PowerPointPresentati.pptx
- SPC统计过程控制程序.pptx
- SPC统计方法基础知识.pptx
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功
评论4