OptiStruct设计:追求高效与轻量化
OptiStruct设计过程中的优化是一个关键环节,特别是在工程设计实践中。OptiStruct作为一款强大的结构分析软件,其优化功能允许求解器为每个元素计算等效密度,这个等效密度范围从0(无材料)到1(100%材料)。优化的目标是最大化结构的性能,同时最小化材料使用,尤其是在承受较低应力区域。求解器会优先考虑降低那些对外来单元影响较小的区域的等效密度,从而实现设计的轻量化和高效能。 在汽车、飞机、包装、消费品等不同行业,设计优化有着显著差异。例如,汽车设计强调驾驶感受、安全性、燃油经济性和成本控制,而航空航天部门则注重性能提升,如速度、耐久性和材料选择(如陶瓷、复合材料等)。包装设计则需平衡美学与成本,同时满足运输安全和空间效率的需求。 CAE(计算机辅助工程)在这个过程中扮演了核心角色,它贯穿整个产品设计周期,从概念草图到详细模型再到最终测试。典型的CAE支持的产品设计循环包括以下步骤: 1. **概念阶段**:开始于初步的概念草图,设计师在此阶段提出初步设计想法,确定性能目标和约束条件。 2. **初步设计**:通过CAE进行结构分析,评估设计的可行性,确定初步的材料分布和布局,可能涉及到优化迭代。 3. **详细设计**:在满足性能指标的同时,进一步细化设计,包括优化结构形状、尺寸和材料,以降低成本和减轻重量。 4. **分析与验证**:使用OptiStruct进行强度、刚度、振动等多物理场分析,确保设计符合安全标准,并可能进行流体力学或热力学模拟。 5. **原型制作与测试**:根据分析结果制造样品,进行实际性能测试,收集数据以验证CAE模型的准确性,并进行必要的调整。 6. **生产准备与优化**:将优化后的设计转化为生产图纸,同时可能再次进行优化以适应生产线和成本效益。 在整个设计过程中,CAE不仅提升了设计效率,还通过迭代优化实现了产品的性能提升和成本节约,确保设计师能在有限的时间和预算内,创造出更具竞争力的产品。因此,OptiStruct的优化功能对于现代工程设计至关重要。
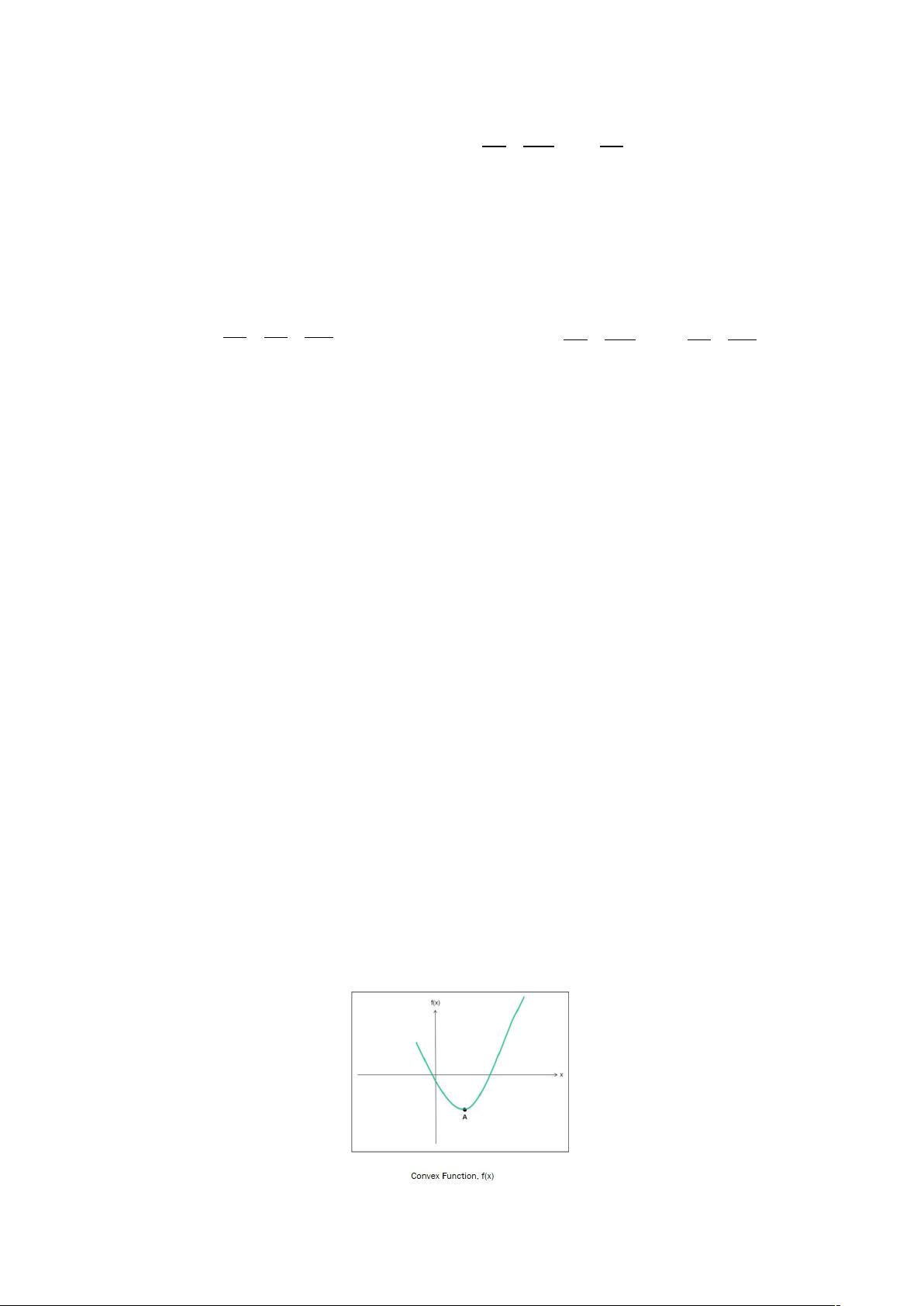
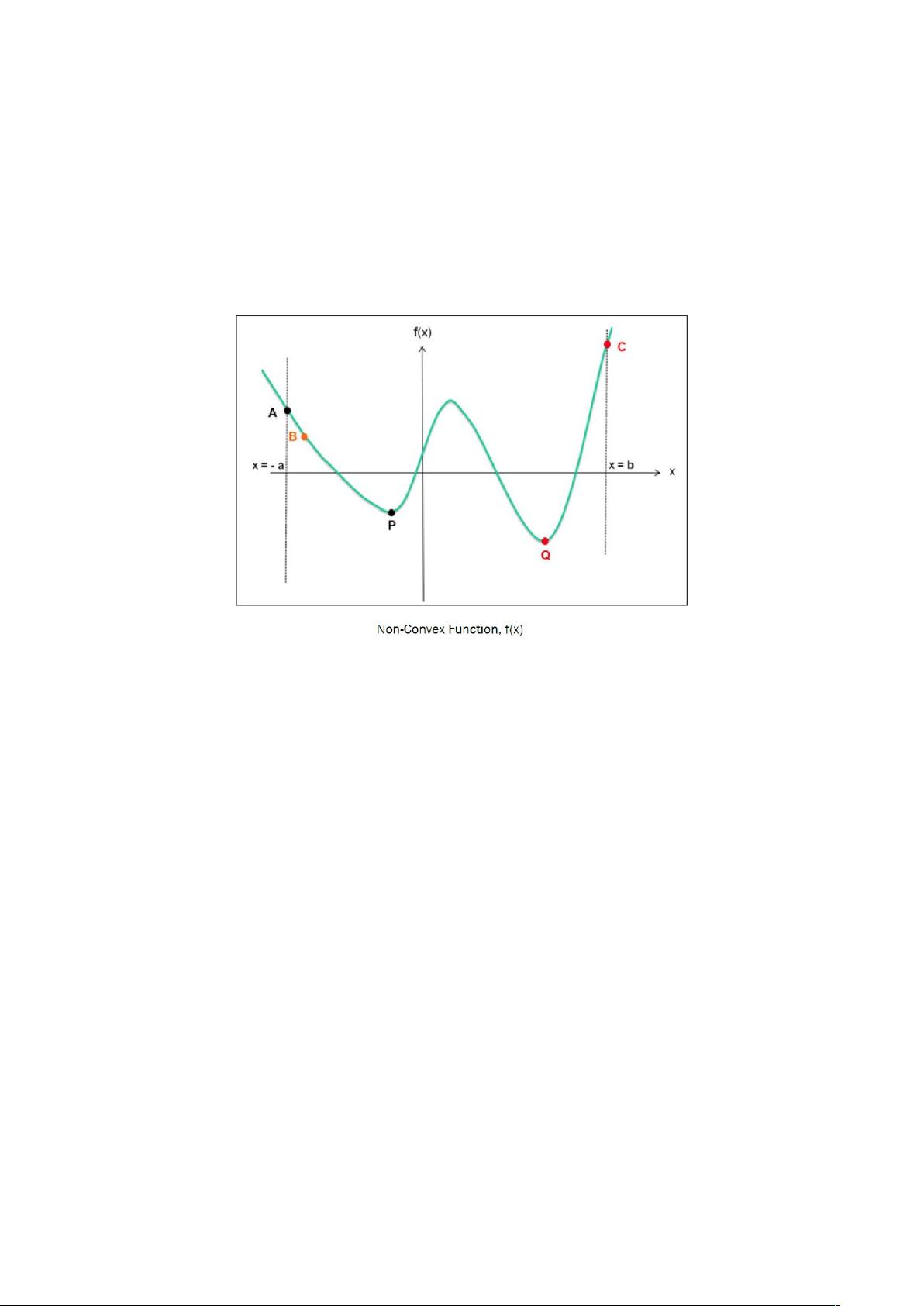
剩余30页未读,继续阅读
- 粉丝: 1
- 资源: 1
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

最新资源
- Vue实现iOS原生Picker组件:详细解析与实现思路
- Arduino蓝牙小车:参数调试与功能控制
- 百度Java面试精华:200页精选资源涵盖核心知识点
- Swift使用CoreData填坑指南:CoreData在Swift 3.0的变化
- 微距离无线充电器创新设计及其实验探索
- MTK Android平台开发全攻略:44步详解流程
- RecyclerView全面解析:替代ListView的新选择
- Android开发:自动适配中英文键盘解决方案
- Android调用WebService接口教程
- Android开发:BitmapUtil图片处理全解析与实例
- Android多线程断点续传实现详解
- PCA算法在人脸识别会议签到系统中的应用
- EventBus 3.0:Android事件总线详解与实战应用
- Android FileUtil:全面解析文件操作实用技巧与实例
- RecyclerView添加头部和尾部实战教程
- Android实现微博滑动固定顶部栏实战与优化


 信息提交成功
信息提交成功