MATLAB实现Floyd算法求最短路径解析

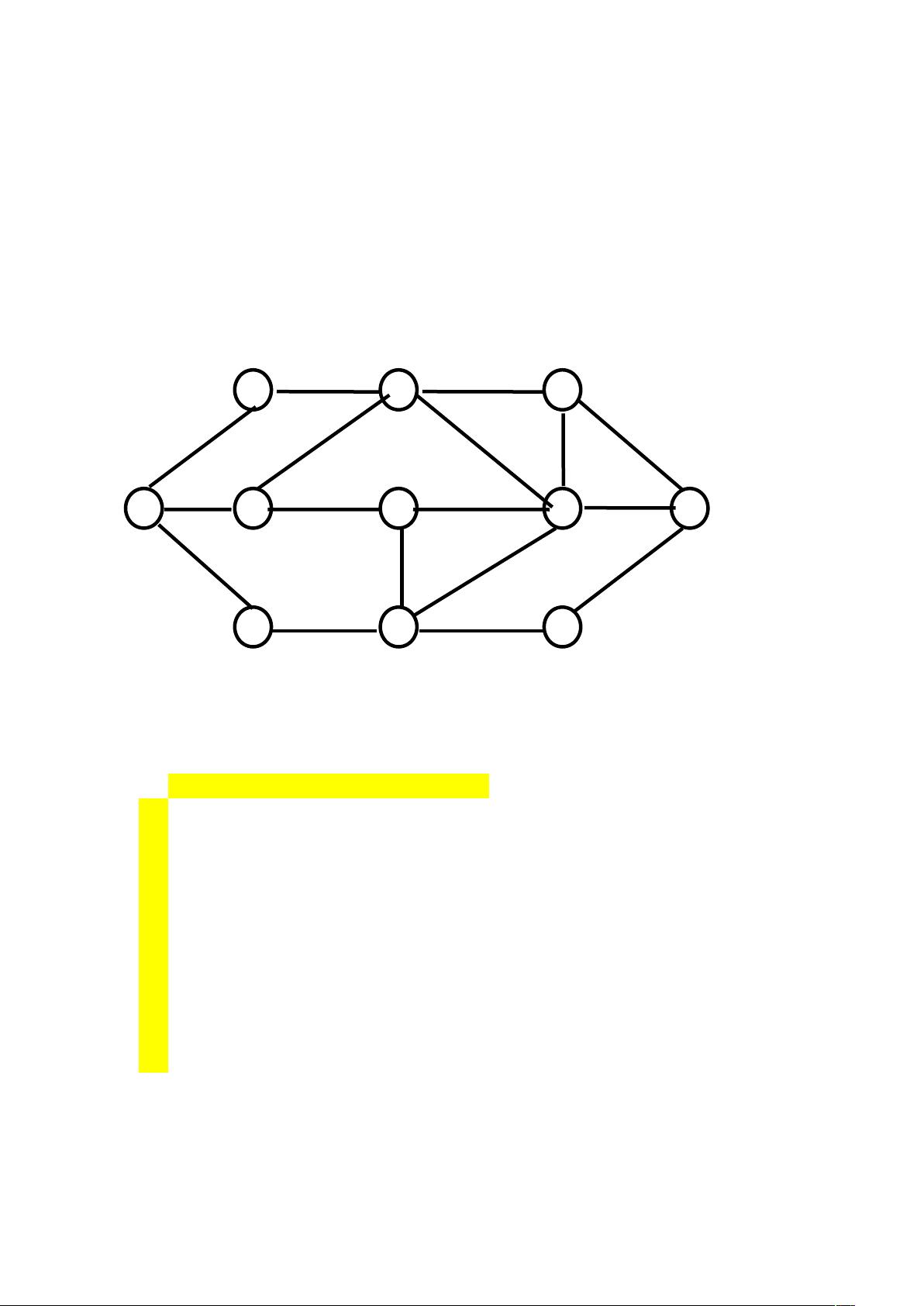
"这篇资源是关于使用MATLAB实现Floyd算法来寻找图中两点间最短路径的介绍，包括一个交通网络的例子和相应的MATLAB程序代码。" Floyd算法，也称为Floyd-Warshall算法，是一种用于解决图中所有顶点对之间的最短路径问题的动态规划算法。在图论和计算机科学中，这个算法可以找到两个节点之间是否存在路径，以及如果存在的话，这条路径的最短距离是多少。Floyd算法的基本思想是逐步考虑所有可能的中间节点，以更新最短路径信息。 在给定的例子中，我们有一个交通网络，其中每个节点代表一个位置，每条弧上的数字表示节点间的旅行时间。为了应用Floyd算法，首先需要将这个网络转化为一个距离矩阵，其中矩阵的每个元素表示对应节点间的距离。对于不直接相连的节点，我们将距离设置为无穷大（在MATLAB中通常用`inf`表示）。 接下来，我们来看MATLAB程序的主要步骤： 1. 清空并初始化全局变量`globalarry`和`arry`，`arry`用于保存路径序号。 2. 用户输入起点和终点的序号。 3. 通过`load`函数读取名为`Distance.txt`的文件，这个文件应该包含了距离矩阵。 4. 调用名为`floyd`的函数，该函数执行Floyd算法。 5. `floyd`函数内部会进行以下操作： - 初始化一个与输入距离矩阵相同大小的新矩阵，用于存储逐步计算出的最短路径信息。 - 对于每一个节点k（从1到节点数量n），遍历所有节点i和j： - 如果通过节点k能更短地到达j，即`D[i,j] > D[i,k] + D[k,j]`，则更新`D[i,j] = D[i,k] + D[k,j]`。 - 在遍历结束后，矩阵`D`中存储了所有顶点对的最短路径距离。 6. 输出从起点到终点的最小距离。 在MATLAB程序中，`floyd`函数会返回两个结果：`D`矩阵（最短距离）和`path`（可能的最短路径的序号）。通过`fprintf`函数，可以显示计算出的最小距离。 Floyd算法的时间复杂度是O(n^3)，因为它涉及到三层嵌套循环，每一层循环都是节点的数量n。虽然对于大型图来说这可能会较慢，但在许多情况下，特别是在节点数量不是特别大的时候，它是一个非常实用且有效的解决方案。 这篇资源提供了Floyd算法的一个实际应用案例，通过MATLAB代码展示了如何处理交通网络中的最短路径问题，对于学习和理解Floyd算法及其在实践中的应用非常有帮助。