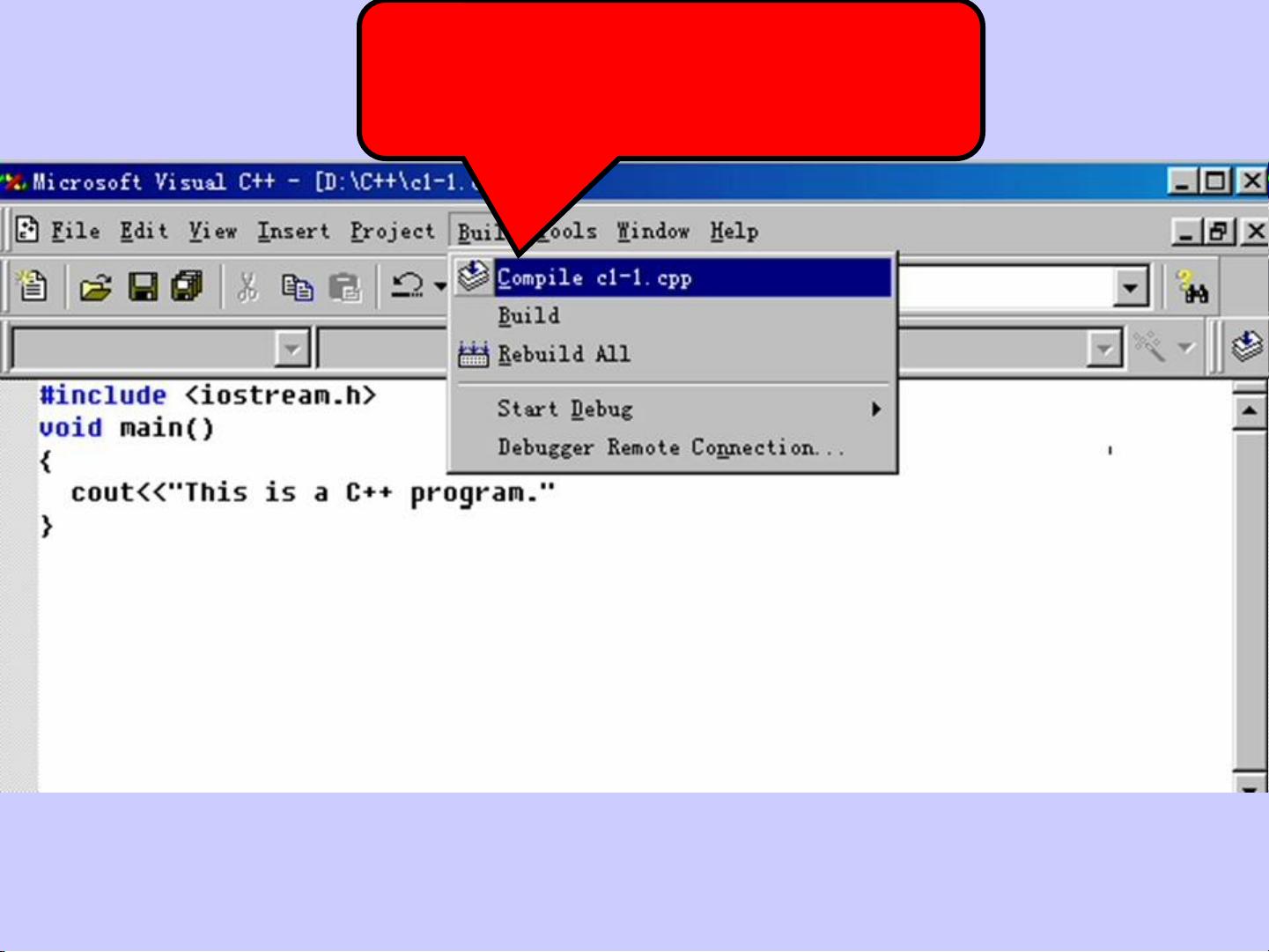
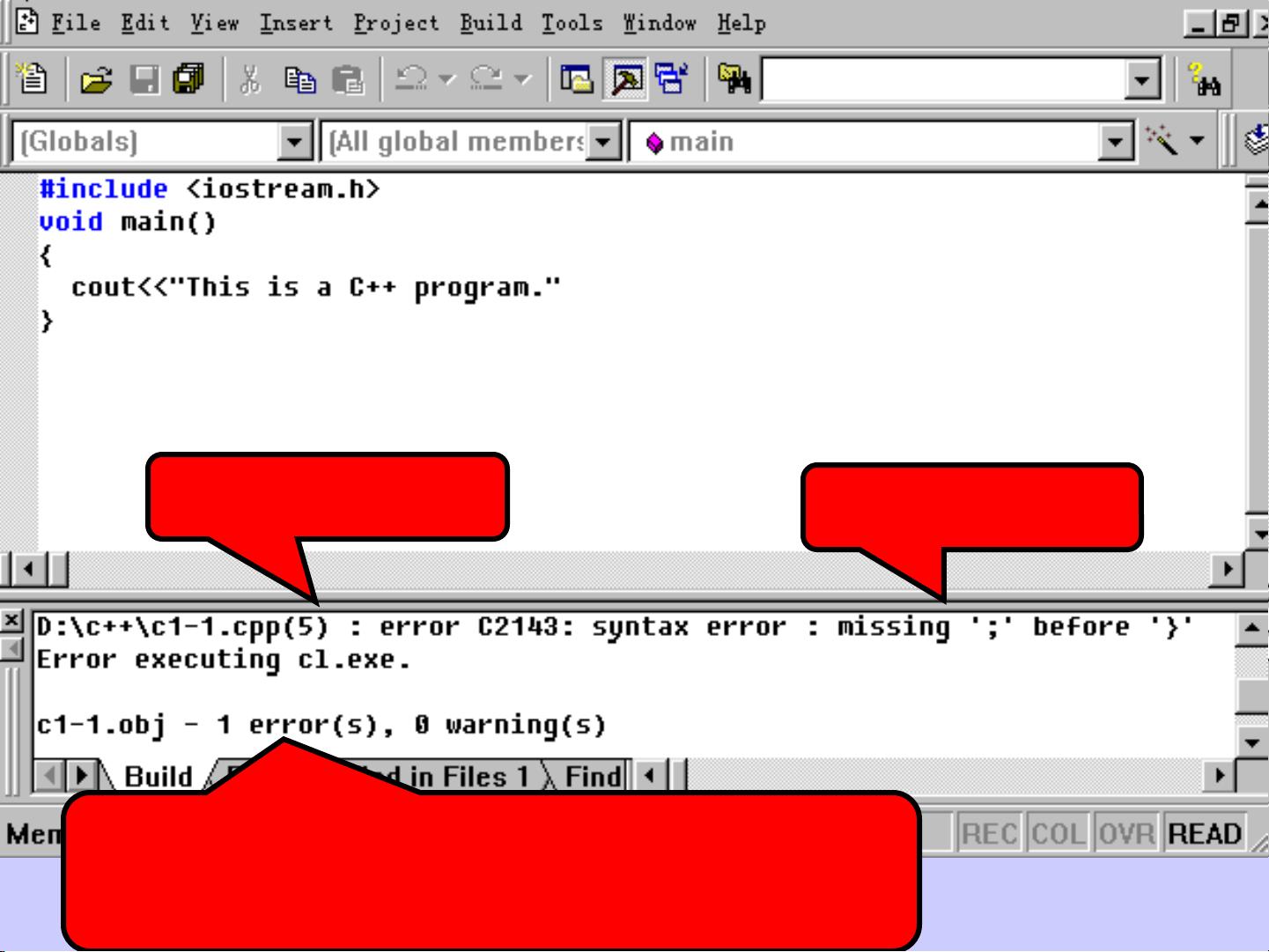
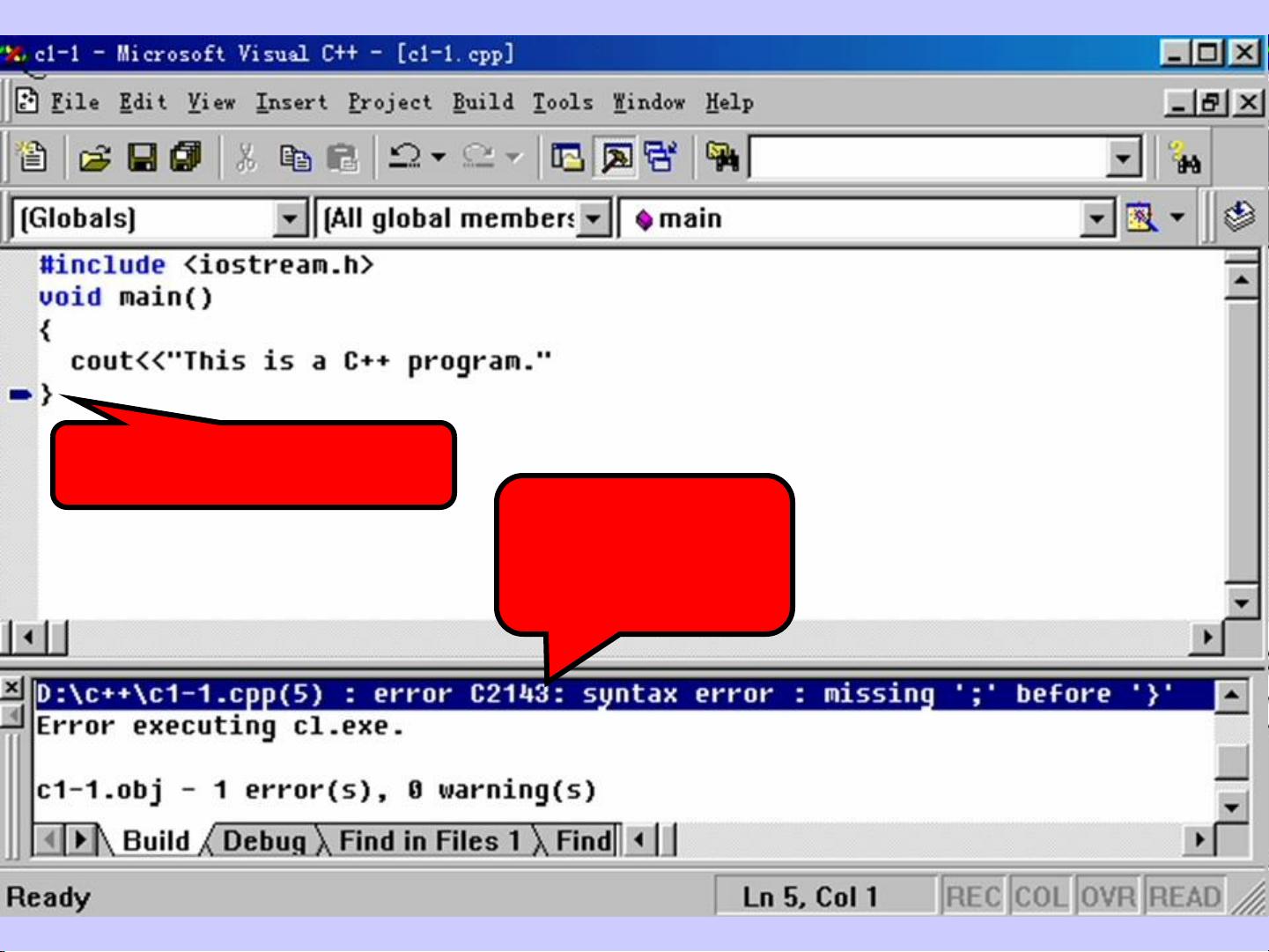
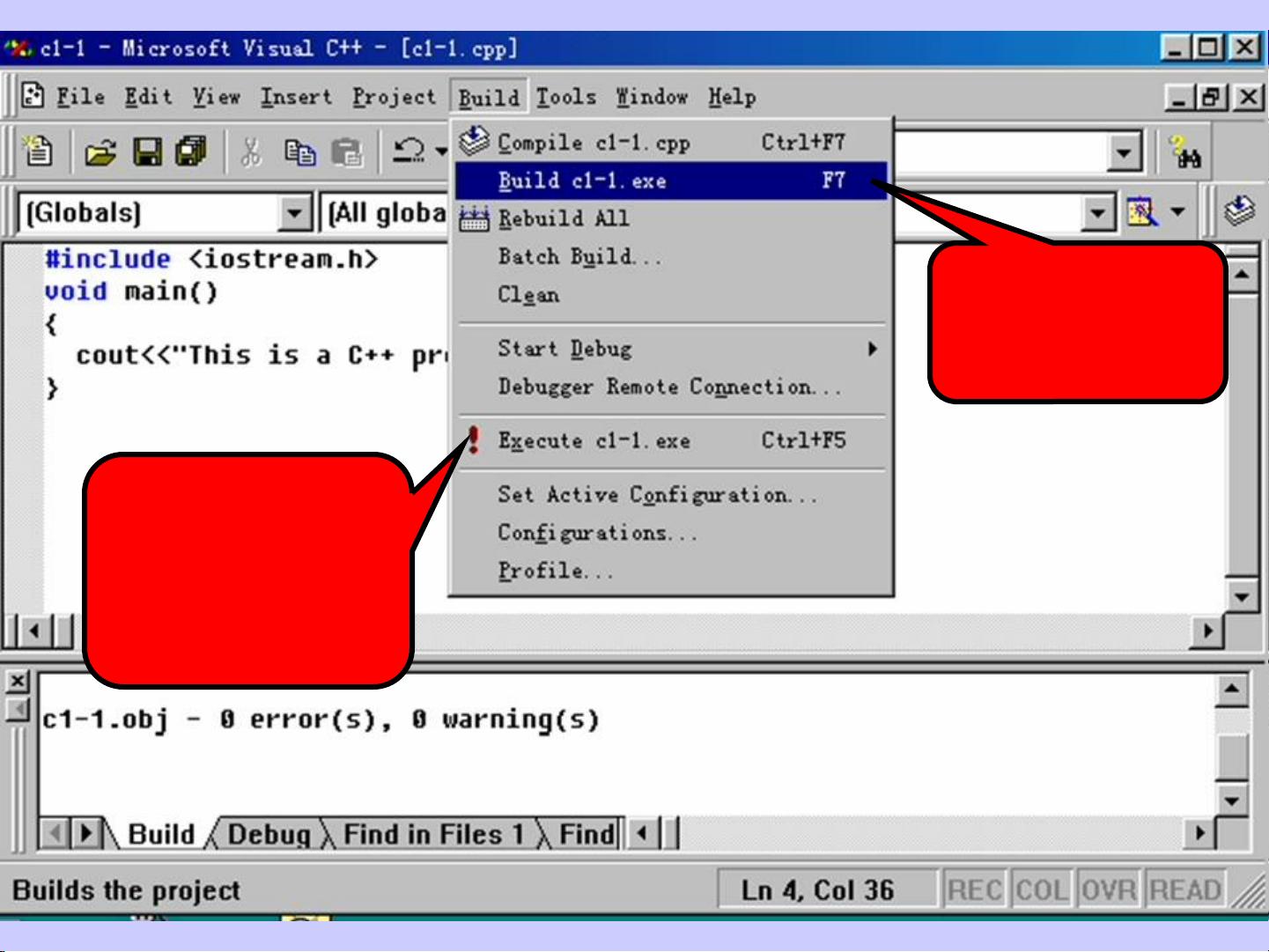
使用递归求解n!-c的程序设计方法

递归方法是一种在程序设计中经常使用的技术，它可以简化问题的解决过程。递归的思想是将一个大的问题拆分成一个或多个更小的子问题，并通过对子问题的递归调用来求解整个问题。在这个过程中，每一次递归调用都是在一个更小的范围内求解这个问题，直到达到基本情况，然后逆向逐步返回，将小的解合并成最终的解。 在给定的任务中，要使用递归方法求解n!-c，其中n表示一个整数，c表示一个常数。首先，我们需要定义一个递归函数fac(n)，它的功能是计算n的阶乘。 函数fac(n)的定义如下： float fac(int n) { float y; if (n == 0 || n == 1) y = 1; else y = n * fac(n-1); return y; } 在这个函数中，如果n等于0或1，那么阶乘的结果是1，这是递归的基本情况；否则，我们通过递归调用fac(n-1)来求解n的阶乘。 接下来，我们需要在主函数main中输入n的值，并调用fac(n)函数来计算n的阶乘。 主函数main的定义如下： void main(void) { float y; int n; cout << "Input n:\n"; cin >> n; cout << n << "! = " << fac(n) << endl; } 在主函数中，我们首先输入一个整数n，然后调用fac(n)来计算n的阶乘，并将结果输出。 例如，我们输入n = 5，那么fac(5)的计算过程如下： fac(5) -> n = 5, y = 5 * fac(4) fac(4) -> n = 4, y = 4 * fac(3) fac(3) -> n = 3, y = 3 * fac(2) fac(2) -> n = 2, y = 2 * fac(1) fac(1) -> n = 1, y = 1 返回y，即5 * (4 * (3 * (2 * 1))) = 120 最终输出为： 5! = 120 总结来说，递归方法是一种有效的问题解决技术，它可以将复杂问题变简单，并通过递归调用和基本情况的判断来求解整个问题。在给定的任务中，我们使用递归方法求解n的阶乘，并通过主函数中的调用来实现。通过这个例子，我们了解了递归方法的思想和应用，以及如何使用递归方法来求解问题。