"连续时间系统的时域分析与数学建模"

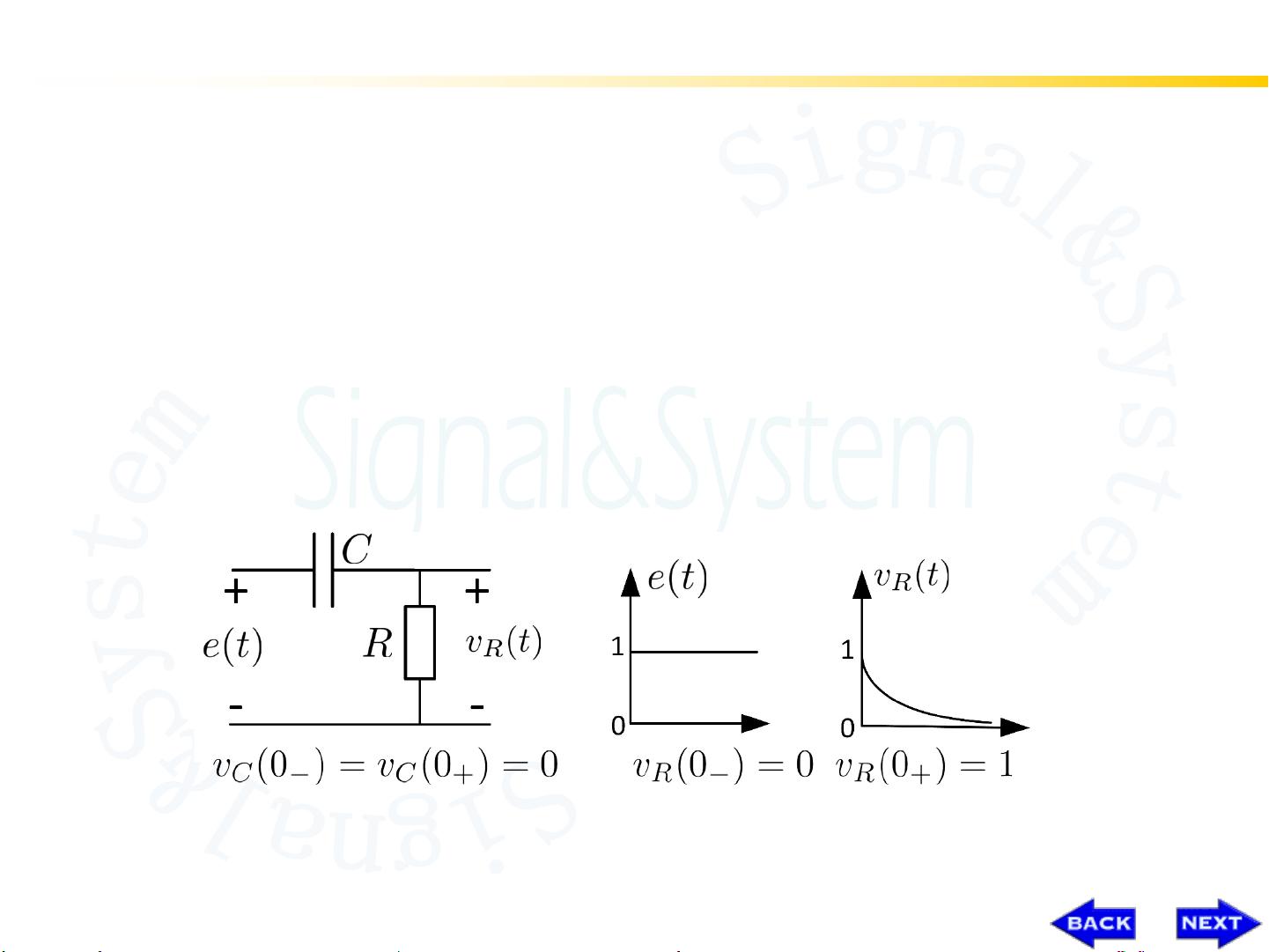
第二章-连续时间系统的时域分析是对线性时不变系统进行分析的方法。该方法包括三个步骤：建立数学模型、运用数学工具处理、给出物理解释。 在建立数学模型的第一步，需要将系统转化为微分方程的形式。对于电气系统，根据电路的基本原理，可以通过电流和电压的关系建立微分方程。例如对于具有电感L、电阻R和电容C的电路，可以得到微分方程： $$\frac{d^2u(t)}{dt^2} + \frac{1}{RC}\frac{du(t)}{dt} + \frac{1}{LC}u(t) = f(t)$$ 其中，u(t)是电压变量，f(t)是输入信号，RC和LC分别为电阻和电容的乘积。这个微分方程可以描述电路的动态行为。 对于机械系统，建立微分方程需要考虑质量、弹簧和阻尼器的作用。例如对于简谐振动的系统，可以得到微分方程： $$\frac{d^2y(t)}{dt^2} + k\frac{dy(t)}{dt} + ky(t) = f(t)$$ 其中，y(t)是位置变量，k是弹簧的劲度系数，f(t)是外力信号。 在第二步，我们可以运用各种数学工具来处理这些微分方程。常见的方法包括拉普拉斯变换、傅里叶变换和微积分等。通过变换，我们可以得到微分方程的解析解，从而获得系统在时域的响应。这些解析解可以揭示系统的特性和行为。 第三步是对这些解析解的物理解释，赋予物理意义。通过分析解析解的形式和参数的意义，我们可以理解系统的稳定性、动态响应、频率响应等特性。例如，对于零输入响应和零状态响应，我们可以分别看到由初始条件和输入信号引发的响应。而冲激响应和阶跃响应可以告诉我们系统的频率特性和阶跃响应的稳定性。 此外，卷积是时域分析中一个重要的运算。它描述了输入信号与系统响应之间的关系。卷积的性质可以帮助我们分析输入信号和输出信号的关系，进一步理解系统的特性。 总之，第二章-连续时间系统的时域分析提供了一种有效的方法，通过建立数学模型、运用数学工具处理和给出物理解释，我们可以深入理解和分析线性时不变系统的特性和行为。以此为基础，我们可以设计出更加优秀和稳定的系统。