1
4
0
5
0
5
4
3
3
5
4
2
1
2
4
5
1
0
4
1
2
4
3
1
2
0
5
5
1
2
0
0 2
3
1
3
4
5
2
4
0
5
1
3
0
5
5
3
1
2
0
0
2
1
5
2
3
5
[12345]
[01345]
[01235]
[02345]
[01245]
[01234]
left
right
front
back
top
bottom
)
<latexit sha1_base64="E+ql3SgwjIInsFzh7/ZNPWlwHRk=">AAAB8nicbVBNS8NAEJ3Ur1q/qh69BIvgqSQi6LHoxWMVWwtpKJvtpl262Q27E6WE/gwvHhTx6q/x5r9x2+agrQ8GHu/NMDMvSgU36HnfTmlldW19o7xZ2dre2d2r7h+0jco0ZS2qhNKdiBgmuGQt5ChYJ9WMJJFgD9Hoeuo/PDJtuJL3OE5ZmJCB5DGnBK0UdO/4YIhEa/XUq9a8ujeDu0z8gtSgQLNX/er2Fc0SJpEKYkzgeymGOdHIqWCTSjczLCV0RAYssFSShJkwn508cU+s0ndjpW1JdGfq74mcJMaMk8h2JgSHZtGbiv95QYbxZZhzmWbIJJ0vijPhonKn/7t9rhlFMbaEUM3trS4dEk0o2pQqNgR/8eVl0j6r+17dvz2vNa6KOMpwBMdwCj5cQANuoAktoKDgGV7hzUHnxXl3PuatJaeYOYQ/cD5/AJEbkW0=</latexit>
<latexit sha1_base64="E+ql3SgwjIInsFzh7/ZNPWlwHRk=">AAAB8nicbVBNS8NAEJ3Ur1q/qh69BIvgqSQi6LHoxWMVWwtpKJvtpl262Q27E6WE/gwvHhTx6q/x5r9x2+agrQ8GHu/NMDMvSgU36HnfTmlldW19o7xZ2dre2d2r7h+0jco0ZS2qhNKdiBgmuGQt5ChYJ9WMJJFgD9Hoeuo/PDJtuJL3OE5ZmJCB5DGnBK0UdO/4YIhEa/XUq9a8ujeDu0z8gtSgQLNX/er2Fc0SJpEKYkzgeymGOdHIqWCTSjczLCV0RAYssFSShJkwn508cU+s0ndjpW1JdGfq74mcJMaMk8h2JgSHZtGbiv95QYbxZZhzmWbIJJ0vijPhonKn/7t9rhlFMbaEUM3trS4dEk0o2pQqNgR/8eVl0j6r+17dvz2vNa6KOMpwBMdwCj5cQANuoAktoKDgGV7hzUHnxXl3PuatJaeYOYQ/cD5/AJEbkW0=</latexit>
<latexit sha1_base64="E+ql3SgwjIInsFzh7/ZNPWlwHRk=">AAAB8nicbVBNS8NAEJ3Ur1q/qh69BIvgqSQi6LHoxWMVWwtpKJvtpl262Q27E6WE/gwvHhTx6q/x5r9x2+agrQ8GHu/NMDMvSgU36HnfTmlldW19o7xZ2dre2d2r7h+0jco0ZS2qhNKdiBgmuGQt5ChYJ9WMJJFgD9Hoeuo/PDJtuJL3OE5ZmJCB5DGnBK0UdO/4YIhEa/XUq9a8ujeDu0z8gtSgQLNX/er2Fc0SJpEKYkzgeymGOdHIqWCTSjczLCV0RAYssFSShJkwn508cU+s0ndjpW1JdGfq74mcJMaMk8h2JgSHZtGbiv95QYbxZZhzmWbIJJ0vijPhonKn/7t9rhlFMbaEUM3trS4dEk0o2pQqNgR/8eVl0j6r+17dvz2vNa6KOMpwBMdwCj5cQANuoAktoKDgGV7hzUHnxXl3PuatJaeYOYQ/cD5/AJEbkW0=</latexit>
<latexit sha1_base64="E+ql3SgwjIInsFzh7/ZNPWlwHRk=">AAAB8nicbVBNS8NAEJ3Ur1q/qh69BIvgqSQi6LHoxWMVWwtpKJvtpl262Q27E6WE/gwvHhTx6q/x5r9x2+agrQ8GHu/NMDMvSgU36HnfTmlldW19o7xZ2dre2d2r7h+0jco0ZS2qhNKdiBgmuGQt5ChYJ9WMJJFgD9Hoeuo/PDJtuJL3OE5ZmJCB5DGnBK0UdO/4YIhEa/XUq9a8ujeDu0z8gtSgQLNX/er2Fc0SJpEKYkzgeymGOdHIqWCTSjczLCV0RAYssFSShJkwn508cU+s0ndjpW1JdGfq74mcJMaMk8h2JgSHZtGbiv95QYbxZZhzmWbIJJ0vijPhonKn/7t9rhlFMbaEUM3trS4dEk0o2pQqNgR/8eVl0j6r+17dvz2vNa6KOMpwBMdwCj5cQANuoAktoKDgGV7hzUHnxXl3PuatJaeYOYQ/cD5/AJEbkW0=</latexit>
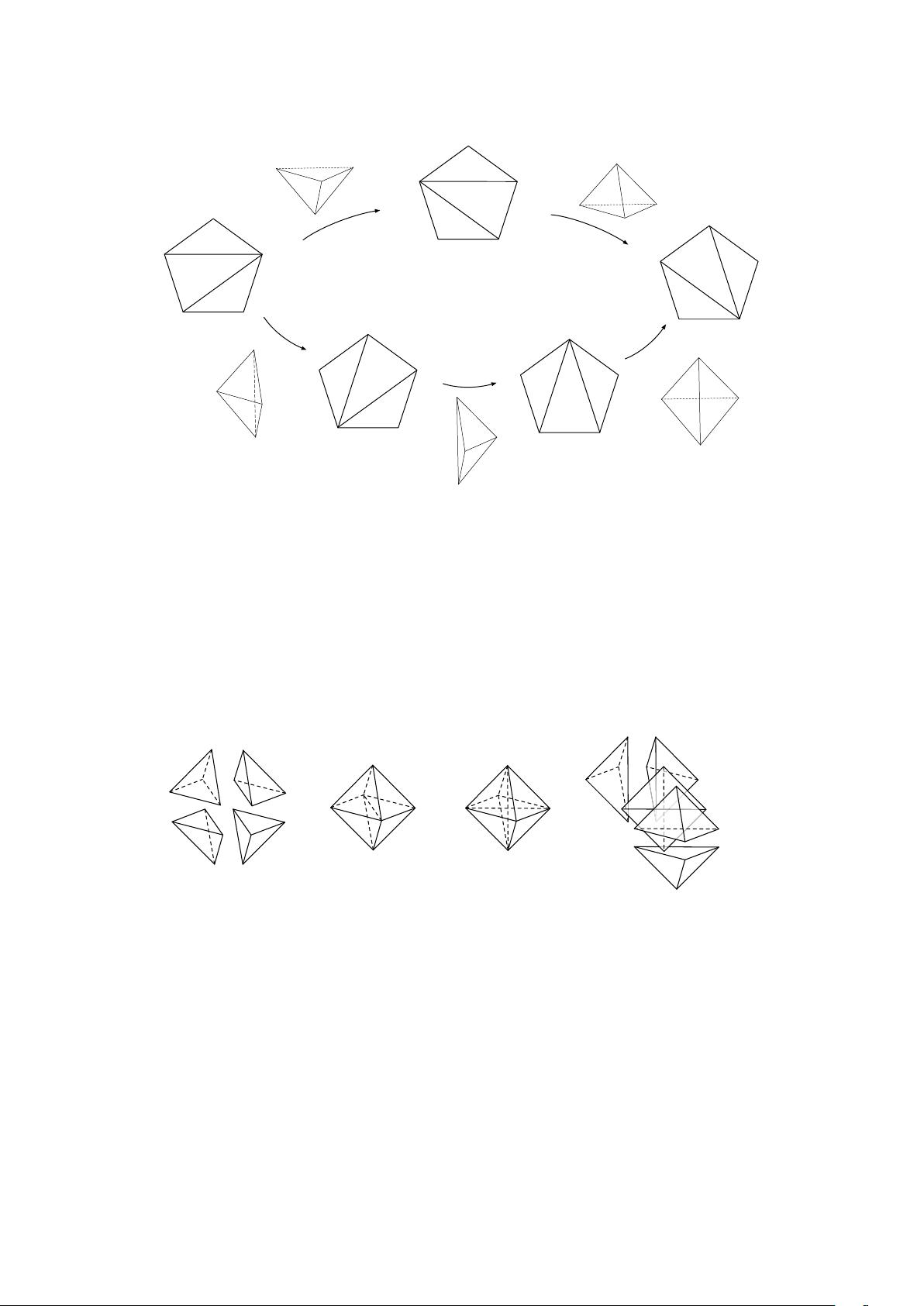
Figure 3. The (3,3) Pachner move, interpreted as relation between sequences of (2,3) and (3,2)
moves.
∂
(∂∆
5
)
−
; put differently, they are internal 3-faces in the triangulation of (∂∆
5
)
−
. The
actual boundary ∂
(∂∆
5
)
−
consists of the remaining nine tetrahedra,
∂
(∂∆
5
)
−
=
[2345] ∪ [1245] ∪ [0345] ∪ [0145]
← oct
−
∪
[1234] ∪ [0134] ∪ [0235] ∪ [0125] ∪ [0123]
← oct
+
(2.10)
We split the boundary as indicated into two octahedra oct
±
. The first octahedron, trian-
gulated into four tetrahedra, is shown on the far left of figure 3. The second octahedron,
triangulated into five tetrahedra, is shown on the far right of figure 3.
Successive cobordisms through the three pentachora [12345], [01345], [01235] may now
be interpreted as a sequence of (2,3) and (3,2) Pachner moves that take us from oct
−
to oct
+
. This sequence of moves is shown in the top part of figure 3. Explicitly, cobor-
dism through [12345] is a (2,3) move; cobordism through [01345] is a (3,2) move; and
cobordism through [01235] is another (2, 3) move. Note that the three internal tetrahedra
[1345], [1235], [0135] that appeared twice in (2.9) all play a role in figure 3. Namely, they
are the tetrahedra that are both ‘created’ and subsequently ‘annihilated’ by moves in the
top sequence.
Similarly, we may compute the triangulated boundary of (∂∆
5
)
+
by first considering
∂[02345] = [2345] ∪ [0345] ∪ [0245] ∪ [0235] ∪ [0234]
∂[01245] = [1245] ∪ [0245] ∪ [0145] ∪ [0125] ∪ [0124]
∂[01234] = [1234] ∪ [0234] ∪ [0134] ∪ [0124] ∪ [0123]
(2.11)
After removing the internal (repeated) tetrahedra, we find
∂
(∂∆
5
)
+
=
[2345] ∪ [1245] ∪ [0345] ∪ [0145]
← oct
−
∪
[1234] ∪ [0134] ∪ [0235] ∪ [0125] ∪ [0123]
← oct
+
= ∂
(∂∆
5
)
−
.
(2.12)
– 9 –