计算机模拟设计摆线轮：理论齿廓与优化

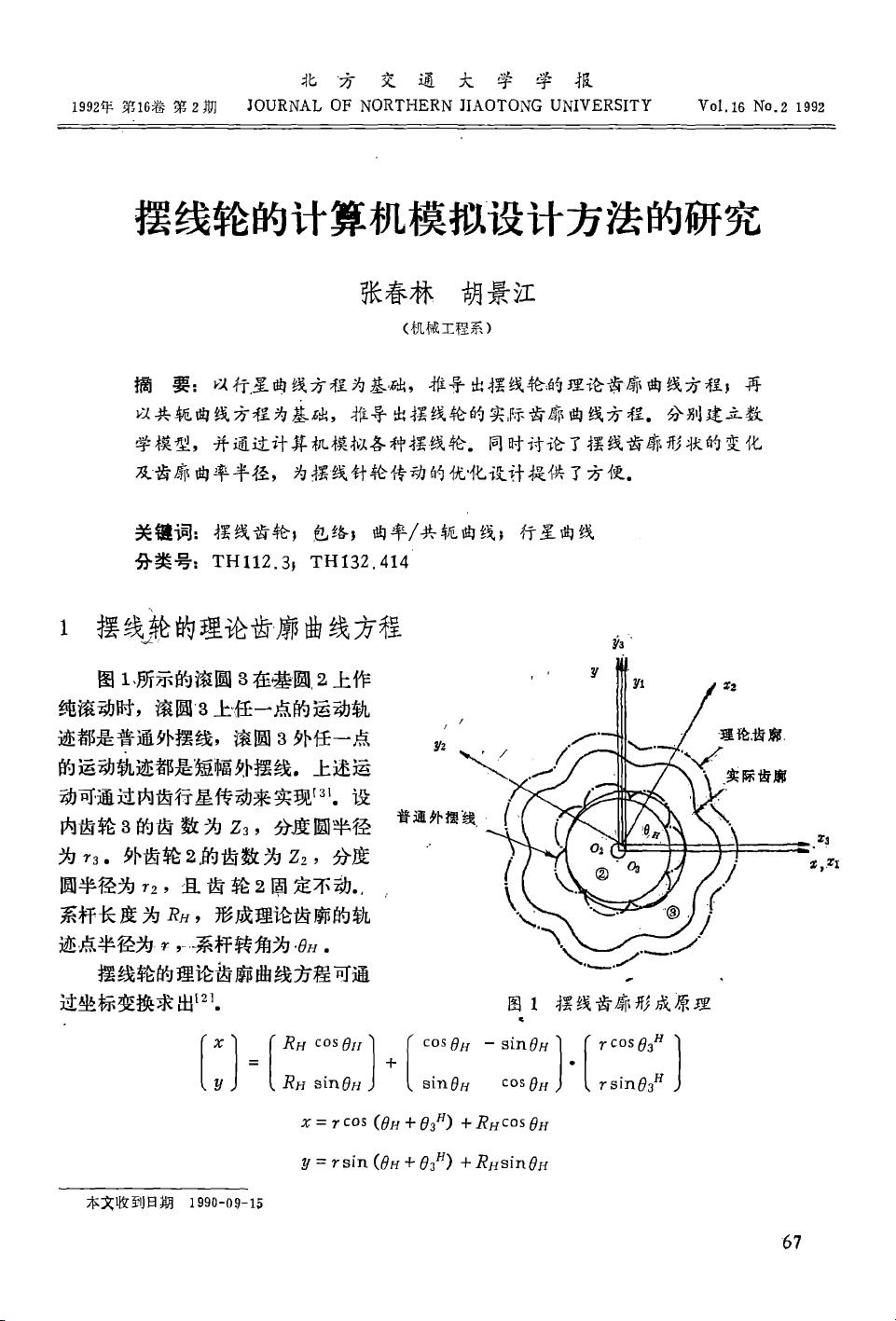
"该研究基于1992年的一篇自然科学论文，主要探讨了摆线轮的计算机模拟设计方法，包括理论齿廓曲线方程的推导、实际齿廓曲线方程的建立以及通过数学模型进行计算机模拟。此外，文章还讨论了摆线齿廓形状变化和曲率半径对摆线针轮传动优化设计的影响，为相关领域的设计提供了便利。" 摆线轮的计算机模拟设计是机械工程领域中的一个重要研究课题，尤其在精密传动装置中，摆线轮因其独特的齿廓形状和优良的传动性能而备受关注。这篇1992年的研究由张春林和胡景江撰写，发表于《北方交通大学学报》。研究的核心是利用行星曲线方程和共轭曲线方程来建立摆线轮的理论和实际齿廓曲线。 首先，摆线轮的理论齿廓曲线方程的推导基于行星曲线方程。当一个小圆（滚圆3）在大圆（基圆2）上作纯滚动时，小圆上任意点的运动轨迹形成普通外摆线，而大圆外任一点的运动轨迹则形成短幅外摆线。通过内齿行星传动机制，可以实现这种运动。研究中假设内齿轮8的齿数为Z3，外齿轮2的齿数为Z2，且满足Z3 - 2Z2 = 1的关系，以确保滚圆和基圆之间的正确啮合。 接下来，通过坐标变换，研究者得到了摆线轮的理论齿廓曲线方程，其中涉及到滚圆半径r、系杆长度RH和系杆转角8H。这些参数与滚圆上的齿数Z3和基圆上的齿数Z2密切相关，且系杆长度RH等于(Z3 - Z2)/2。进一步，通过系杆转角的改变，可以模拟不同齿数的摆线轮。 然后，实际齿廓曲线方程的推导基于共轭曲线方程，这使得摆线轮的齿形更符合实际工况。研究者还讨论了摆线齿廓形状的变化，包括曲率半径的影响，这对于优化摆线针轮传动系统至关重要，因为曲率半径直接影响到传动效率和磨损情况。 最后，该研究提出了如何根据摆线轮的齿数和系杆运动周期来选择合适的行星传动机构，例如，为了得到7齿摆线轮，可以选择22 = 7，Z3 = 8的设置，此时系杆需转动8周以形成完整的7齿摆线。 这篇研究提供了摆线轮设计的理论基础和计算机模拟方法，为优化摆线针轮传动系统的性能和设计提供了有力的工具，对于提高传动效率和可靠性具有实际应用价值。