无监督学习：邻居嵌入与流形学习

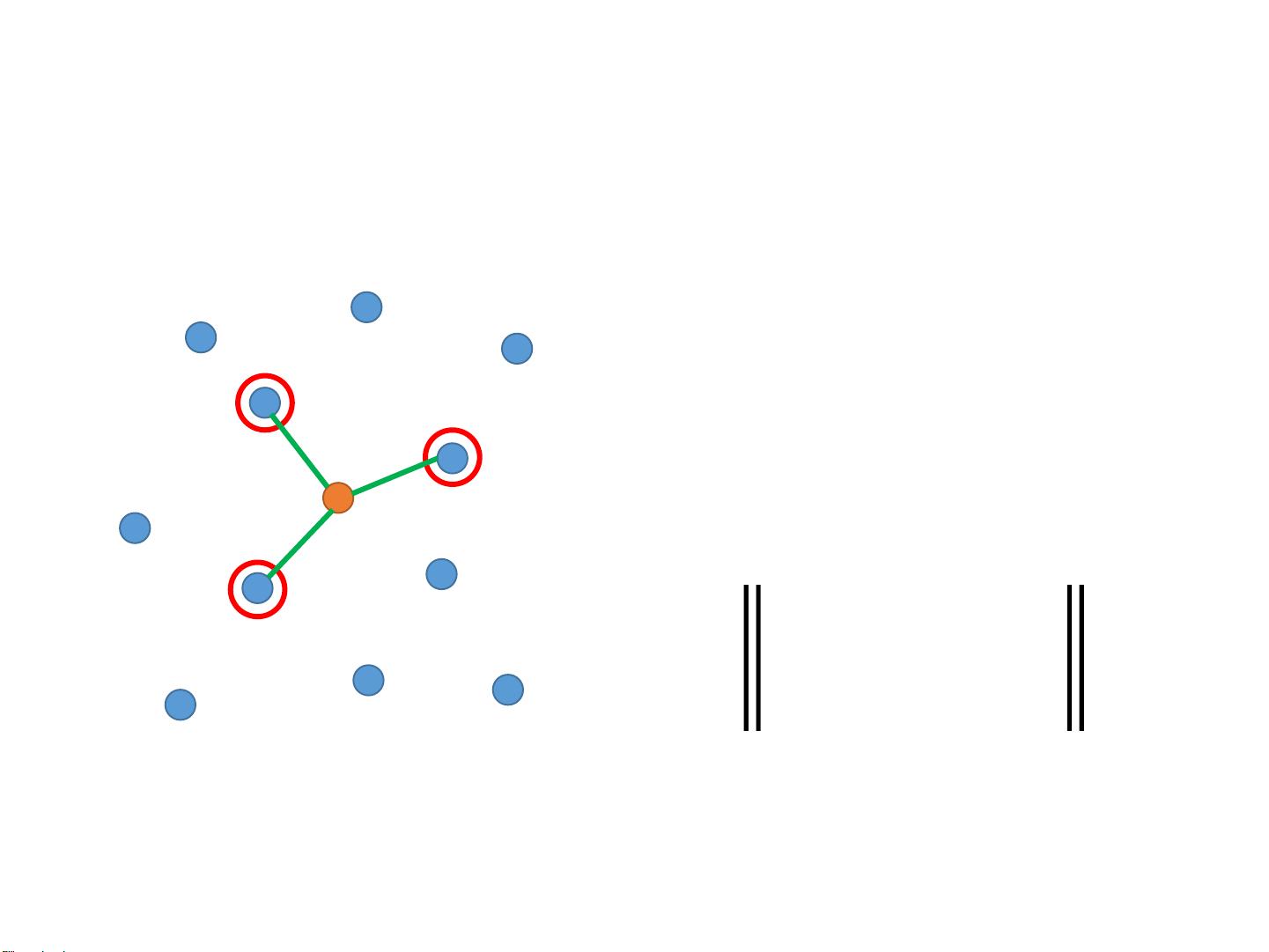
"这篇资源主要探讨了无监督学习中的邻居嵌入方法，包括流形学习、局部线性嵌入（LLE）以及拉普拉斯特征映射。这些技术主要用于降维和数据可视化，尤其适用于聚类和后续的监督学习任务。" 在机器学习领域，无监督学习是研究数据内在结构和模式的一种方法，不依赖于预先标注的类别信息。邻居嵌入是无监督学习的一种策略，其目标是将高维数据转换到低维空间，同时保持数据点之间的相对邻近关系。这种方法有助于发现数据的潜在结构，并且在处理大规模复杂数据时尤其有用。 流形学习是无监督学习的一个子领域，假设数据在高维空间中是沿着一个低维的流形分布的。通过流形学习，我们可以从原始的高维数据中提取出这个低维流形，使得数据更易于理解和分析。常见的流形学习方法包括局部线性嵌入（LLE）和拉普拉斯特征映射。 局部线性嵌入（LLE）是一种保留局部结构的非线性降维技术。它假设数据点的邻域内存在线性关系。在LLE中，首先找到每个数据点的邻居，然后通过最小化邻近点在新空间中的重构误差来确定低维表示。具体来说，对于数据点 \( \mathbf{x_i} \) 和其邻居 \( \mathbf{x_j} \)，权重 \( w_{ij} \) 表示它们之间的关系。LLE的目标是找到低维空间中的 \( \mathbf{z_i} \) 和 \( \mathbf{z_j} \)，使它们的加权距离与原始空间中的距离尽可能接近。 拉普拉斯特征映射是一种基于图的降维方法，它构建了一个数据点之间的图，其中边的权重表示数据点间的距离。该距离在流形上进行近似。拉普拉斯矩阵 \( L \) 反映了数据点的光滑度，其可以分为对角度量矩阵 \( D \) 和邻接矩阵 \( W \) 的差。在半监督学习中，拉普拉斯特征映射可以用于传播标签信息，因为如果两个数据点在高密度区域接近，那么它们的标签很可能相同。 这些无监督学习技术提供了一种理解数据内在结构的方式，为聚类、数据可视化和后续的监督学习任务提供了有力工具。无论是LLE还是拉普拉斯特征映射，它们都致力于在低维空间中捕捉高维数据的复杂关系，从而简化数据分析并揭示隐藏的模式。