Bézier曲线详解：从数学原理到编程实现

"《计算机图形学》中的Bézier曲线生成算法探究与实现，涵盖了该曲线的发展历史、公式推导、应用以及二次和三次Bézier曲线的源代码实例。" Bézier曲线是计算机图形学中不可或缺的一部分，主要用于创建平滑、连续的二维图形。这些曲线以其发明者Pierre Bézier的名字命名，他在1962年将其引入到工业设计领域，特别是在汽车设计中。Bézier曲线基于伯恩斯坦多项式，这些多项式能够近似任何连续函数，而且随着多项式的阶数增加，逼近效果更佳。 伯恩斯坦多项式是伯恩斯坦基函数的组合，它们构成了一组在[a, b]区间上的正交基，允许我们用多项式来表示和逼近任意函数。在计算机图形学中，这些多项式用于构建Bézier曲线的数学模型，使得曲线可以通过调整控制点的位置来改变形状，而无需重新计算整个曲线。 Paul de Casteljau在1959年提出的de Casteljau算法是计算Bézier曲线的一种数值稳定方法。这个算法通过递归地在控制点之间进行线性插值，最终生成曲线上的点。由于其稳定性，de Casteljau算法在实际应用中非常流行。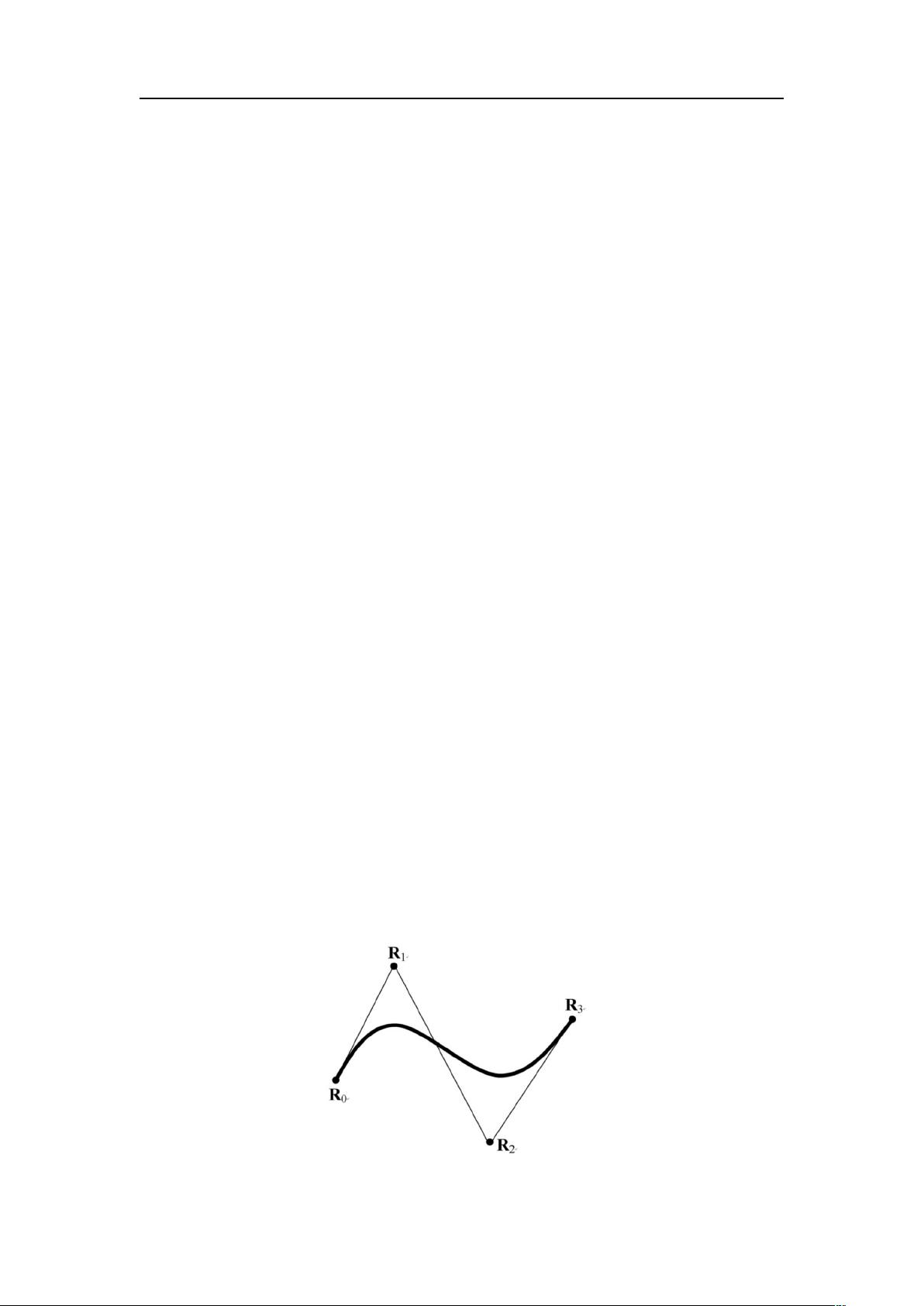 Bézier曲线的定义包括起始点和终止点（锚点），以及控制点。这些控制点影响曲线的形状，但并不直接位于曲线上。曲线在锚点处开始和结束，而控制点则决定了曲线的弯曲方向和程度。在二维图形软件中，用户可以通过移动控制点来直观地编辑曲线的形状，这使得Bézier曲线成为图形设计工具的核心组成部分，例如在Adobe Photoshop和Flash等软件中。 在《计算机图形学》的描述中，还提到了Bézier曲线在自由曲线设计中的重要性。相比于插值样条曲线，Bézier曲线提供了更大的灵活性，因为它们可以通过控制点来调整，而不是严格地通过每个给定点。这在需要精细调整和创造平滑曲线的设计场景中尤其有用。 二次和三次Bézier曲线是最常见的类型，分别由三个和四个控制点定义。二次曲线通常用于简化表示，而三次曲线则能更好地模拟复杂形状。提供的源代码示例可能包含如何使用这些基础曲线进行图形绘制的程序片段，对于理解Bézier曲线的实现原理非常有帮助。 Bézier曲线是计算机图形学中一种强大的工具，它结合了理论数学和实用几何，使得设计师和开发者能够精确地创建和操控二维图形。通过对Bézier曲线的理解和应用，我们可以构建出更加美观、真实的视觉效果，广泛应用于游戏开发、UI设计、动画制作等领域。