透视投影下的摄像头、图像与世界坐标系转换详解

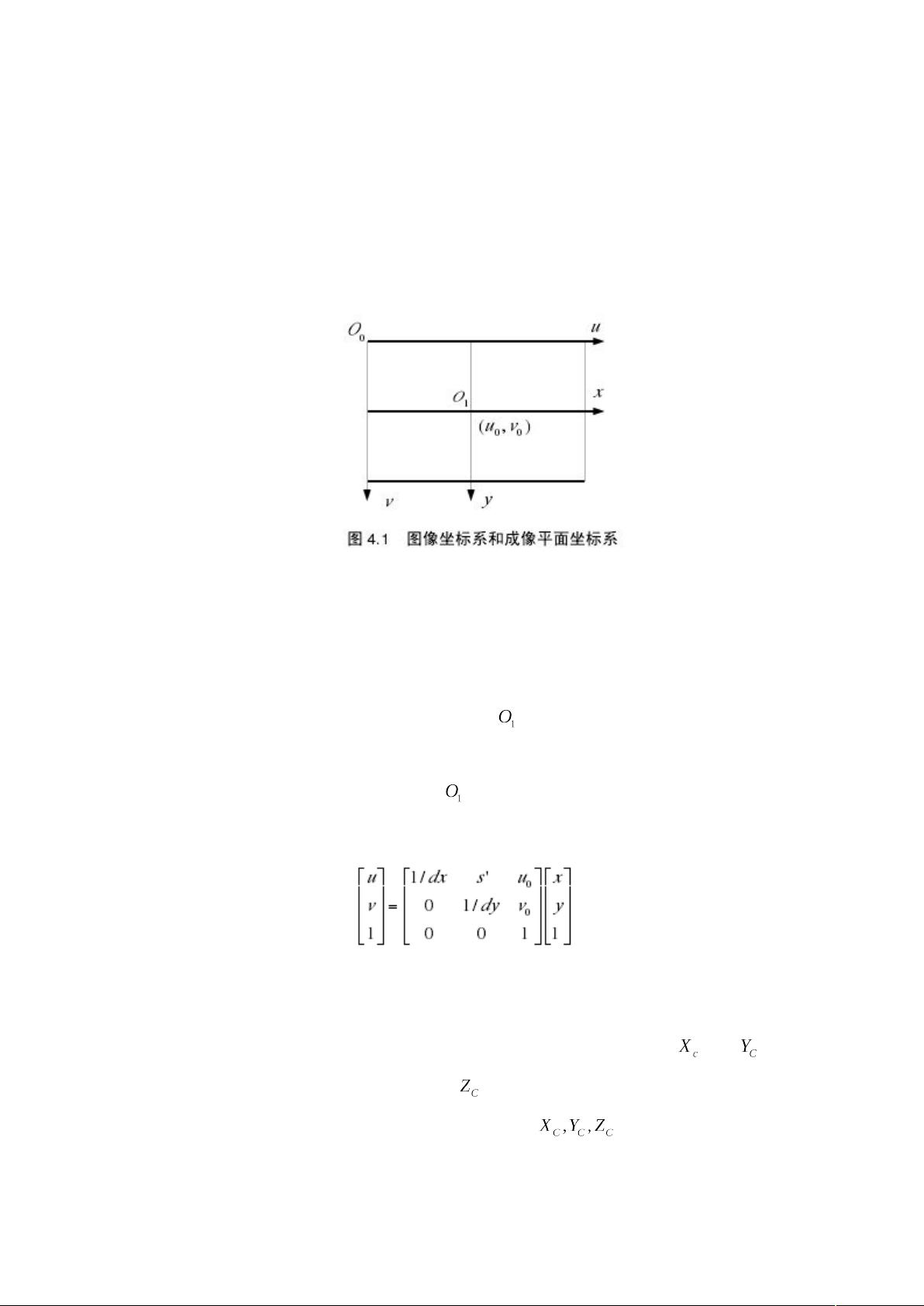
本文主要探讨了摄像头坐标系、图像坐标系以及世界坐标系在计算机视觉和机器人技术中的关键作用。首先，图像坐标系（Pixel coordinatesystem）是数字化图像的基础，以像素(u, v)的形式表示，其中u和v分别对应图像数组中的列和行，这是图像数据的基本存储结构。这个坐标系以像素为单位，反映的是图像内部的逻辑布局。 接着，成像平面坐标系（Retinal coordinatesystem）是对图像坐标系的补充，引入了物理单位（如厘米），用(x, y)表示。它的原点设在摄像机光轴和图像平面的交点——主点，通常位于图像中心，但可能存在偏差。在这个坐标系中，每个像素有相应的物理尺寸dx和dy，同时考虑到摄像机成像面的倾斜特性，引入了倾斜因子(s')。 摄像机坐标系(Cameracoordinatesystem)更为具体，以摄像机的光心O为中心，轴线与成像平面坐标系平行，其中[pic]轴垂直于图像平面。光轴与图像平面的交点是主点O'，整个系统构成一个直角坐标系，焦距由OO'表示。这个坐标系用于描述摄像机的几何特性。 最后，世界坐标系(Worldcoordinatesystem)是描述实际物理空间中物体和摄像机位置的参照系。它与摄像机坐标系之间的转换通过旋转矩阵R和平移向量t来实现，这些参数共同构成了空间点在两种坐标系中的变换关系。摄像机的线性模型通常采用透视投影，它基于针孔成像原理，所有场景光线汇聚于一个投影中心，这在计算机图形学和机器视觉的应用中至关重要。 总结来说，理解并掌握这些坐标系的转换对于处理图像处理、三维重建、目标检测等任务至关重要，它们构成了计算机视觉和机器人技术中不可或缺的数学基础。通过这些坐标间的转换，能够将图像中的像素位置映射到现实世界的物理空间，从而实现精确的定位和交互。