图算法探索:深度优先搜索与广度优先搜索
需积分: 10 111 浏览量
更新于2024-07-22
收藏 20.28MB PDF 举报
"关于无向图的算法介绍,包括图的API、深度优先搜索、广度优先搜索以及连通分量的探讨"
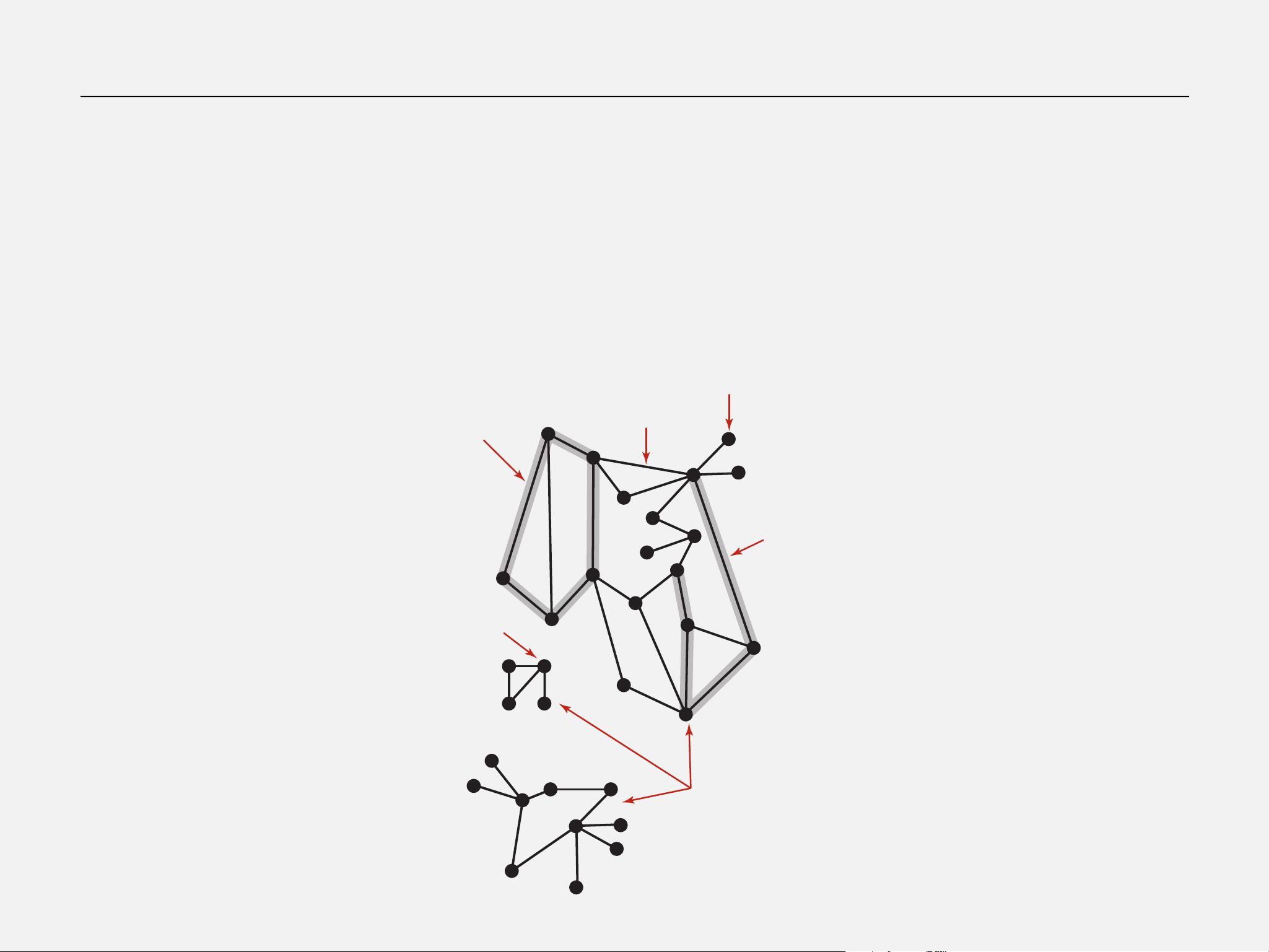
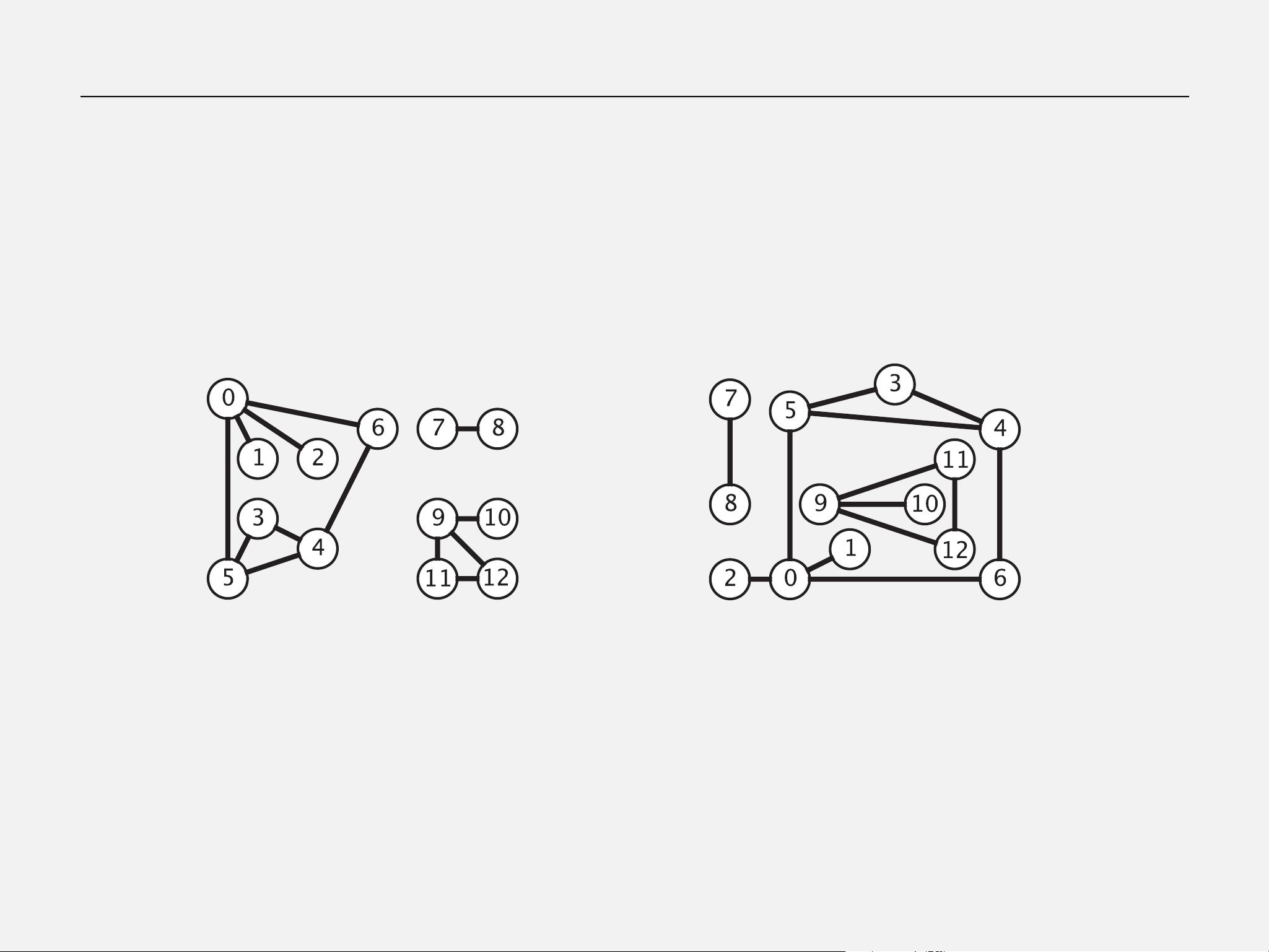
在计算机科学中,无向图是一种重要的数据结构,它由一组顶点(vertices)和顶点之间的边(edges)构成,边没有特定的方向。无向图的研究是因其在众多实际应用中的广泛性和其作为抽象问题解决工具的强大能力。从社交网络到蛋白质相互作用网络,再到科学研究领域,无向图的模型可以有效地表示各种实体之间的关系。
无向图的API(Application Programming Interface)通常包括以下基本操作:
1. 添加顶点(addVertex):用于向图中添加新的顶点。
2. 添加边(addEdge):用于连接两个顶点,创建无向边。
3. 获取邻接顶点(adjacentVertices):返回给定顶点的所有邻接顶点列表,即与该顶点相连的其他顶点。
4. 判断连通性(isConnected):检查两个顶点之间是否存在路径。
5. 删除顶点或边:根据需求移除图中的顶点或边。
深度优先搜索(Depth-First Search, DFS)是一种遍历无向图的方法,从某个起点开始,尽可能深地探索图的分支,直到达到叶子节点,然后回溯到上一个未访问的节点,继续深入。DFS常用于检测图中的环路、找到最短路径等任务。
广度优先搜索(Breadth-First Search, BFS)则从起点开始,逐层遍历所有相邻的顶点,然后再扩展到下一层。BFS在寻找最短路径、查找最近的邻居等问题中非常有效。
连通分量(Connected Components)是无向图中的一个重要概念,指的是图中任意两个顶点都存在路径相连的顶点集合。在一个图中可能有多个连通分量,通过BFS或DFS可以找出所有的连通分量。
挑战方面,设计和分析无向图算法时,需要考虑时间复杂性和空间复杂性,以及如何处理大规模图数据。例如,对于社交网络中的大型图,如何在有限的内存中进行有效的遍历和计算,以及如何优化搜索算法以提高效率,都是实际应用中常见的挑战。
总结来说,无向图的算法是计算机科学和离散数学的重要研究领域,它们在理解现实世界中的复杂关系网络、解决实际问题中起着关键作用。从图的API设计到具体的搜索算法,每一个环节都需要深入理解和巧妙应用,以实现高效、准确的解决方案。
2013-05-16 上传
2019-01-30 上传
2017-05-04 上传
2023-03-29 上传
2023-06-03 上传
2023-06-03 上传
2023-09-05 上传
2023-05-14 上传
2023-07-27 上传
emilytang3101
- 粉丝: 0
- 资源: 1
最新资源
- cygwin,spin,xspin安装全过程记录
- 网络工程师学习笔记(数据通信基础知识)
- Cortex-M3权威指南
- A Simple Methodology for Applying UML to Database Design
- 高质量C/C++编程
- 嵌入式 C/C++语言精华文章集锦
- vs.net使用技巧
- 最小重量机器设计问题
- envi4.5 授权文件 license 绝对可用
- Struts快速学习指南
- C+语言中的指针和内存泄漏
- wimax技术的发展与展望
- struts in action 06
- 计算机故障速查手册(不可缺少的手边工具书)
- 华为_FPGA设计高级技巧Xilinx篇.pdf
- cobol课件 ibm主机系列