Matlab实现电力系统潮流计算

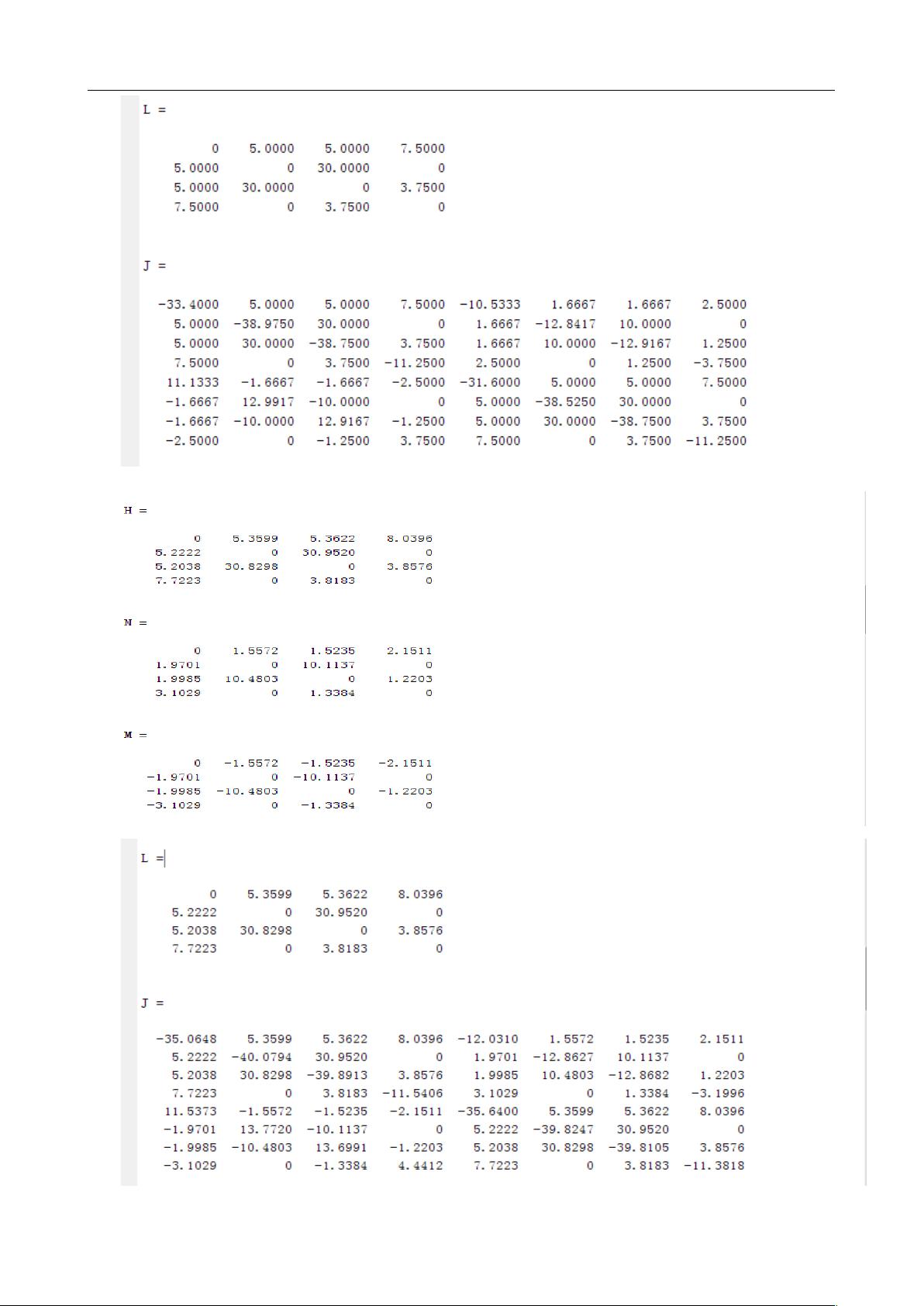
"潮流计算matlab实例计算" 潮流计算是电力系统分析中的一个重要环节，用于确定电力网络在稳态运行条件下各节点电压和支路电流。MATLAB作为一种强大的数学计算工具，常被用于实现电力系统的潮流计算。以下是潮流计算的相关知识点： 1. **牛顿-拉夫逊法**： 牛顿-拉夫逊迭代法是解决非线性方程组，特别是电力系统潮流计算中的关键算法。它基于泰勒级数展开，通过迭代求解电力网络的功率平衡方程来获取节点电压和相角。基本步骤包括： - 构建节点导纳矩阵（Y矩阵），它反映了电网中各元件的电气特性。 - 设定初始电压和相角估计值，通常为额定值。 - 计算功率不平衡量，即实际功率与计算功率之间的差值。 - 形成并更新雅可比矩阵，它是对功率平衡方程的偏导数矩阵。 - 更新节点电压值，通过误差方程求解新的电压不平衡量。 - 迭代过程持续直到满足预设的收敛条件，如电压和功率的相对变化小于一定阈值。 2. **网络节点优化**： 在进行潮流计算时，节点的编号策略会影响到计算效率。常见的优化方法包括： - **静态优化法**：按照节点的出线支路数进行编号，最少出线的节点优先。这种方法有助于减少计算中的非零元素，提高计算效率。 - **动态优化法**：在计算过程中根据节点的特性动态调整编号，例如，通过减少雅可比矩阵的填充率或改进迭代过程。 3. **MATLAB实现**： 在MATLAB中实现潮流计算，通常会涉及以下步骤： - 定义电力网络的拓扑结构，包括发电机、负荷、变压器、线路等元件的参数。 - 使用MATLAB的矩阵运算构建节点导纳矩阵。 - 实现牛顿-拉夫逊迭代算法，包括求解非线性方程组和更新电压的过程。 - 编写设计说明书，详细说明计算过程和结果。 4. **收敛性与稳定性**： 收敛性是牛顿-拉夫逊法的关键指标，不收敛可能是因为初始值选取不合适、网络中有重根或复根、或者迭代过程中的误差处理不当。通过调整初始值、引入下拉因子或选择合适的预处理技术可以改善收敛性。 5. **应用与扩展**： 潮流计算不仅用于确定系统稳态运行状态，还可应用于故障分析、稳定性评估、无功优化等领域。MATLAB提供了丰富的工具箱和函数，如电力系统工具箱（Power System Toolbox），可以帮助用户扩展和定制潮流计算模型。 通过理解和掌握这些知识点，电力工程师能够使用MATLAB有效地进行潮流计算，解决实际电力系统中的各种问题。