深度优先遍历:从邻接矩阵出发的图探索
133 浏览量
更新于2024-08-04
收藏 173KB DOCX 举报
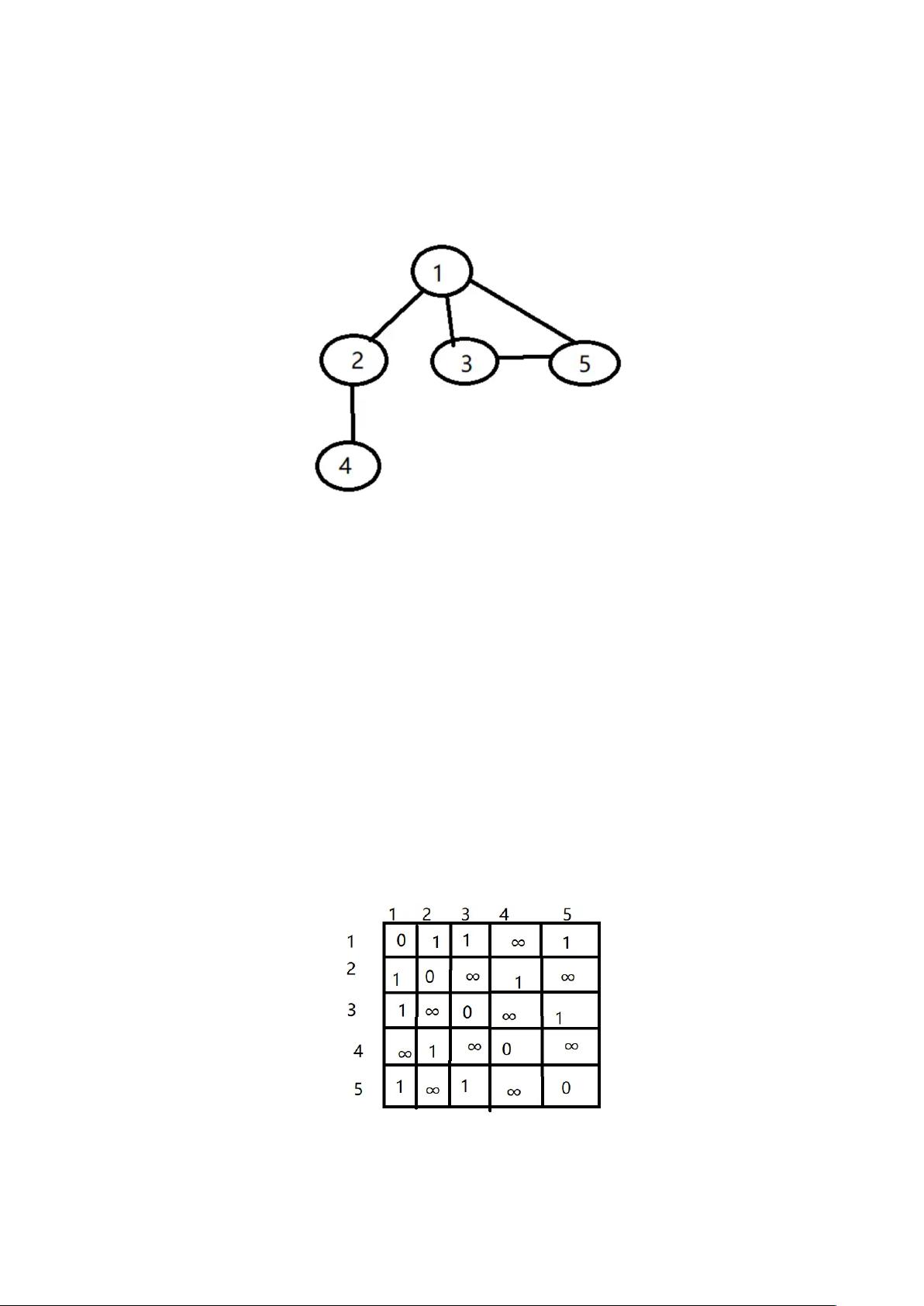
深度优先遍历是一种常用的图算法,它主要用于探索图的连通性,尤其是对于寻找路径、检测环路等问题非常有效。在本题中,我们关注的是如何利用邻接矩阵来实现深度优先遍历。邻接矩阵是一种常见的图数据结构,其中的元素表示顶点间是否存在边,1表示有边,通常无穷大(如999999)表示没有边。这种方法适用于稠密图,即边的数量接近于顶点总数的平方。
深度优先遍历的基本思想是从一个起始顶点开始,尽可能深地搜索图的分支,直到无法再继续为止,然后回溯到其他未访问的顶点。在这个过程中,我们记录每个顶点的访问顺序,时间戳可以用来追踪是第几个访问到某个顶点的。在遍历过程中,我们会标记已访问的顶点,避免重复访问。
在给出的C代码中,程序首先初始化一个二维数组`e`为邻接矩阵,将对角线元素设为0,表示自环,非对角线元素设为无穷大,表示默认没有边。接着,通过循环读入顶点间的边,并更新邻接矩阵。函数`dfs(int cur)`是一个递归函数,接收当前正在访问的顶点编号`cur`作为参数。
在`dfs`函数中,首先将当前顶点标记为已访问(`book[cur] = 1`),然后遍历与`cur`相邻的所有未访问顶点,如果发现新的顶点,继续调用`dfs`函数。当所有与`cur`相连的顶点都访问过,或者无法找到新的未访问顶点时,函数会返回,然后继续处理下一个未访问的顶点,直至遍历完所有顶点。
深度优先遍历通过递归的方式,利用邻接矩阵有效地跟踪了图的拓扑结构,实现了对图的完整遍历。这种遍历方式特别适合用于查找路径或检测图中的连通分量。通过这个例子,我们可以了解如何在实际编程中运用深度优先遍历算法,以及如何利用邻接矩阵来优化存储和查找过程。
点击了解资源详情
点击了解资源详情
点击了解资源详情
2022-06-24 上传
2023-06-01 上传
2023-06-01 上传
2024-06-16 上传
2019-09-12 上传